A particle is performing a linear simple harmonic motion. If the instantaneous acceleration and velocity of the particle are a and v respectively, identify the graph which correctly represents the relation between a and v.

The correct Answer is:C
To solve the problem of identifying the graph that correctly represents the relationship between instantaneous acceleration (a) and velocity (v) of a particle performing simple harmonic motion (SHM), we can follow these steps:
Step 1: Understand the equations of SHM
In simple harmonic motion, the instantaneous velocity (v) and acceleration (a) can be expressed in terms of the maximum velocity (V₀) and angular frequency (ω). The equations are:
- Velocity: v=V0sin(ωt)
- Acceleration: a=−V0ωcos(ωt)
Step 2: Differentiate the velocity equation
To find the relationship between acceleration and velocity, we can differentiate the velocity equation with respect to time:
- The instantaneous acceleration (a) is given by:
a=dvdt=V0ωcos(ωt)
Step 3: Relate acceleration and velocity
From the equations of SHM, we can express the cosine term in terms of sine:
- We can rewrite the acceleration equation as:
a=−V0ω√1−(vV0)2
This shows that acceleration (a) is related to velocity (v) through the maximum velocity (V₀).
Step 4: Square both sides
To eliminate the square root, we can square both sides of the equation:
a2=(−V0ω)2(1−(vV0)2)
This leads to:
a2=V20ω2−a2v2V20
Step 5: Rearranging the equation
Rearranging gives us a linear relationship:
v2V20+a2(V0ω)2=1
This can be interpreted as a circle equation in the a-v plane.
Step 6: Identify the graph
The relationship indicates that as velocity (v) increases, acceleration (a) decreases, and vice versa. The graph of this relationship is a downward-sloping curve. However, when we consider the squares of the variables, we can see that the relationship can also be represented as a straight line in the form:
v2+a2(V0ω)2=constant
This indicates a linear relationship with a negative slope.
Conclusion
From the analysis, we find that the correct graph representing the relationship between acceleration (a) and velocity (v) in simple harmonic motion is a straight line with a negative slope.
In simple harmonic motion, the instantaneous velocity (v) and acceleration (a) can be expressed in terms of the maximum velocity (V₀) and angular frequency (ω). The equations are:
- Velocity: v=V0sin(ωt)
- Acceleration: a=−V0ωcos(ωt)
To find the relationship between acceleration and velocity, we can differentiate the velocity equation with respect to time:
- The instantaneous acceleration (a) is given by:
a=dvdt=V0ωcos(ωt)
From the equations of SHM, we can express the cosine term in terms of sine:
- We can rewrite the acceleration equation as:
a=−V0ω√1−(vV0)2
This shows that acceleration (a) is related to velocity (v) through the maximum velocity (V₀).
To eliminate the square root, we can square both sides of the equation:
a2=(−V0ω)2(1−(vV0)2)
This leads to:
a2=V20ω2−a2v2V20
Rearranging gives us a linear relationship:
v2V20+a2(V0ω)2=1
This can be interpreted as a circle equation in the a-v plane.
The relationship indicates that as velocity (v) increases, acceleration (a) decreases, and vice versa. The graph of this relationship is a downward-sloping curve. However, when we consider the squares of the variables, we can see that the relationship can also be represented as a straight line in the form:
v2+a2(V0ω)2=constant
This indicates a linear relationship with a negative slope.
From the analysis, we find that the correct graph representing the relationship between acceleration (a) and velocity (v) in simple harmonic motion is a straight line with a negative slope.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 More Than One Correct
Explore 8 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 Comprehension
Explore 2 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 1 Subjective
Explore 39 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
While a particle executes linear simple harmonic motion
View SolutionFor a particle executing simple harmonic motion, the acceleration is -
View SolutionA mass M is performing linear simple harmonic motion. Then correct graph for acceleration a and corresponding linear velocity v is
View SolutionIn simple harmonic motion, the ratio of acceleration of the particle to its displacement at any time is a measure of
View SolutionThe x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at t=23s is

View SolutionA particle executes linear. If a and v donate the acceleration and velocity of the particle respectively, then correct graph relating the values a2 and v2 is
View SolutionFor a particle executing simple harmonic motion, the acceleration is proportional to
View SolutionA particle is executing a simple harmonic motion. Its maximum acceleration is α and maximum velocity is β. Then, its time period of vibration will be
View SolutionWhile a particle executes simple harmonic motion, the rate of change of acceleration is maximum and minimum respectively at
View SolutionThe x−t graph of a particle undergoing simple harmonic motion is shown below. The accelertion of the particle at t=4/3s is
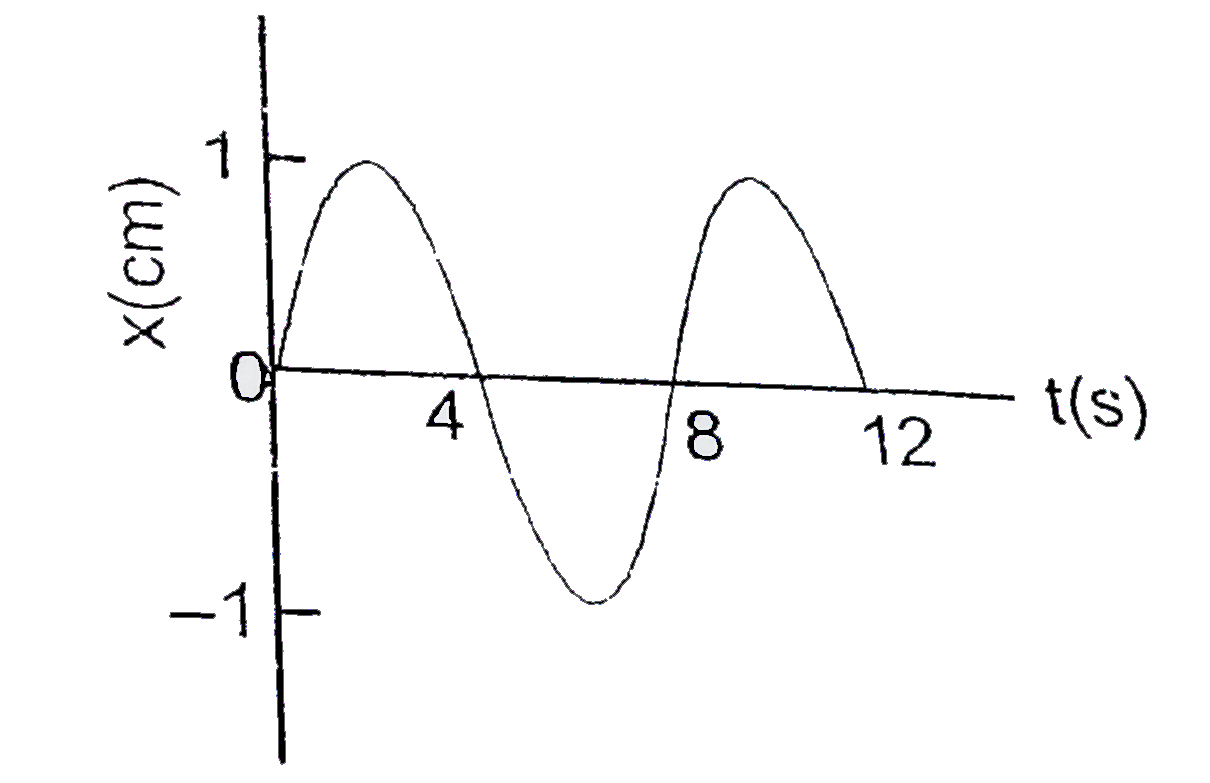
View Solution