A cord is attached between a 0.50 kg block and a string with force constant k=20N/m.The other end of the spring is attrached to the wall and the cord is placed over a pulley (I=0.60MR2) of mass 5.0 kg and radius 0.50 m.(See the accompanying figure.) Assuming no slipping occurs what is the frequency of the oscillations when the body is set into motion ?

The correct Answer is:C
In equilibrium
kx0=mg
∴x0=mgk=0.5×1020
=0.25m
When displaced downwards by x from the mean position, total mechanical energy,
E=−mgx+12mv2+12Iω2+12(x+x0)2
Substituting I=0.6MR2 and ω=vR
We have,
E=−mgx+12mv2+12(0.6MR2)(vR)2+12k(x+x0)2
Since E = constant
∴dEdt=0
or 0=−mg(dxdt)+12m(2v.dvdt)+(0.6M)+(v)dvdt+12k[2(x+x0)]dxdt
putting dxdt=v,kx0=mg and dvdt=a
We have
0=(ma+0.6Ma)+kx
or a=−(km+0.6M)x
Since, a∝−x motion is SHM.
f=12π√∣∣ax∣∣
=12π√km+0.6M
=12π√200.5×0.6×5
=0.38Hz .
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Single Correct
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A mass of 0.2 kg is attached to the lower end of a massless spring of force constant 200Nm the other end of which is fixed to a rigid support. Study the following statements.
View SolutionA block of mass 1 kg is attached to one end of a spring of force constant k = 20 N/m. The other end of the spring is attached to a fixed rigid support. This spring block system is made to oscillate on a rough horizontal surface (μ=0.04). The initial displacement of the block from the equilibrium position is a = 30 cm. How many times the block passes from the mean position before coming to rest ? (g=10m/s2)
View SolutionPassage X) A 2kg block hangs without vibrating at the bottom end of a spring with a force constant of 400 N/m. The top end of the spring is attached to the ceiling of an elevator car. The car is rising with an upward acceleration of 5ms2 when the acceleration suddenly ceases at t=0 and the car moves upward with constant speed. (g=10m/s2)
What is the angular frequency of oscillation of the block after the acceleration ceases?
View SolutionA block of mass m is attached to a massless spring of force constant k, the other end of which is fixed from the wall of a truck as shown in figure. The block is placed over a smooth surface and initially the spring is unstretched. Suddenly the truck starts moving towards right with a constant accleration a0. As seen from the truck

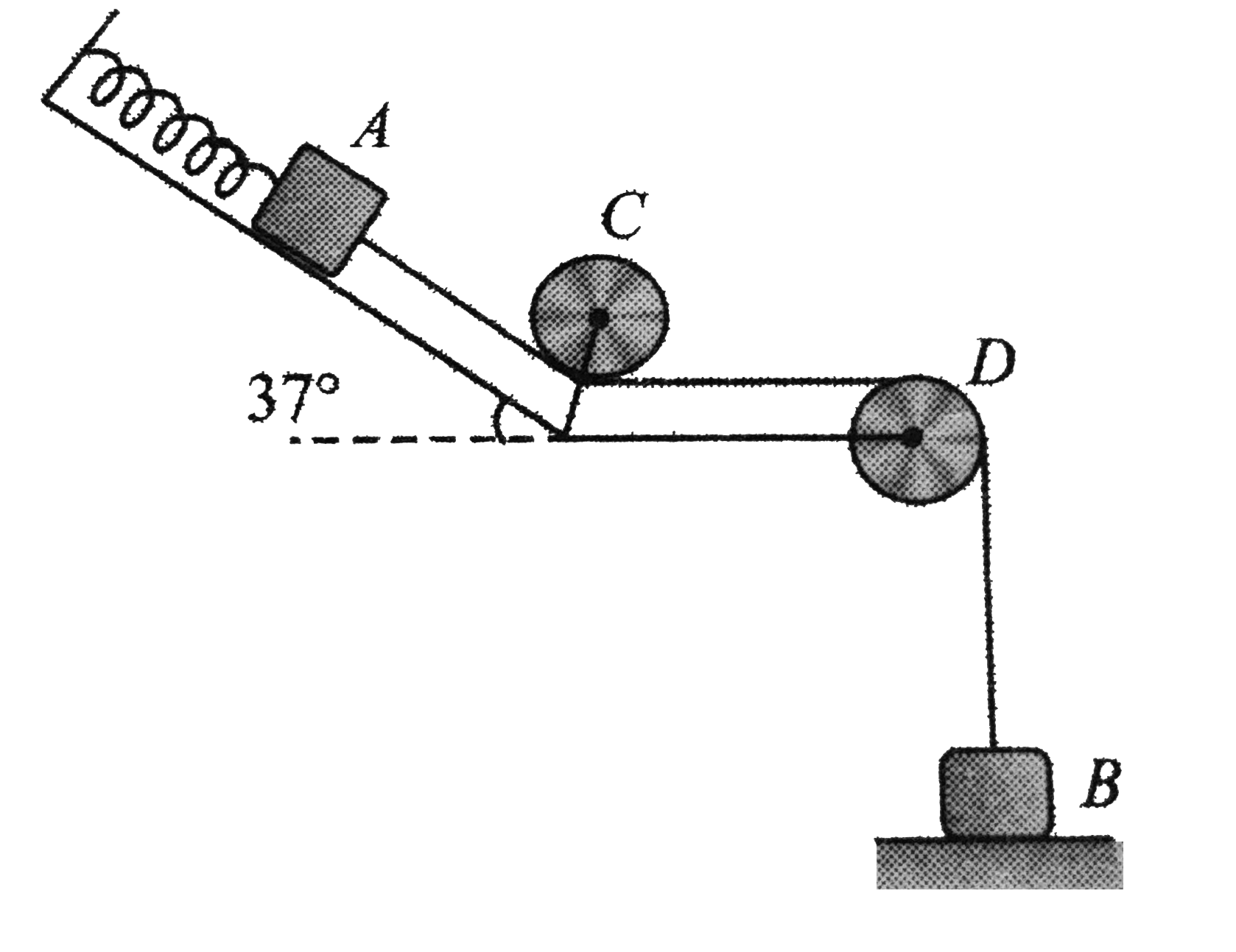
View SolutionA block A of mass m=5kg is attached with a spring having force constant K=2000Nm−1. The other end of the spring is fixed to a rough plane, inclined at 37∘ with horizontal and having coefficient of friction m=0.25. Block A is gently placed on the plane such that the spring has no tension. Then block A is released slowly. Calculate elongation of the spring when equilibrium is achieved. Now an inextensible thread is connected with block A and passes below pulley C and over pulley D, as shown in figure. Other end of the thread is connected with another block B of mass 3kg. Block B is resting over a table and thread is loose. If the table collapse suddenly and B falls freely through 80/9cm, the thread becomes taut, calculate combined speed of blocks at that instant, and maximum elongation of spring in the process of motion. (g=10ms−2).
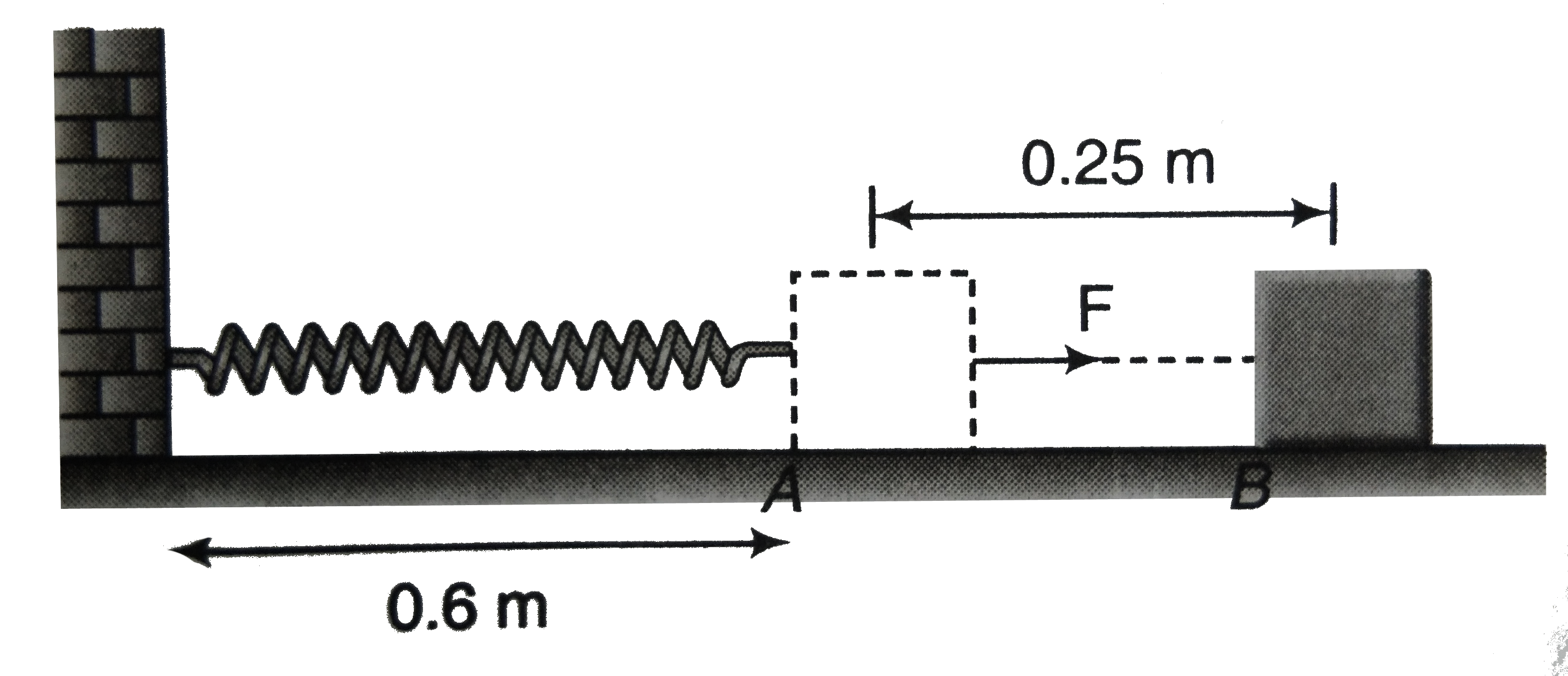
View SolutionA 0.500kg block is attached to a spring with length 0.60m and force constant k=40.0N/m. The mass of the spring is negligible. You pull the block to the right along the surface with a constant horizontal force F=20.0N. (a) What is the block's speed when the block reaches point B,which is 0.25m to the right of right of point A? (b) What the block reaches point B, you let go off the block. In the subsequent motion, how close does the block get to the wall where the lift end of the spring is attached? Neglect size of block and friction.
 .
.
View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View SolutionIn the shown figure mass of the pulley is m and radius 2R. A light concentric spool of radius R is rigidly attached with the pulley. Two blocks A and B having masses m & 4m respectively are attached with the pulley by means of light strings. Lower surface of the block B is attached to a spring of stiffness ka and block B rests on a smooth inclined plane inclined 30∘ with horizontal. Other end of the spring is fixed to the ground. The block A is stretched a small distance and released then find the frequency of the oscillation of block B. (The strings do not slip on the pulley).

View SolutionA block of mass 0.18kg is attached to a spring of force-constant 2N/m. The coefficient of friction between the block and the floor is 0.1 Initially the block is at rest and the spring is un-stretched. An impulse is given to the block as shown in the figure. The block slides a distance of 0.06m and comes to rest for the first time. The initial velocity of the block in m//s is V=N/10. Then N is :
 .
.
View Solution
