Show that the combined spring energy and gravitational energy for a mass m hanging from a light spring of force constant k can be expressed as U0+12ky2, where y is the distance above or below the equilibrium position and U0 is constant.
The correct Answer is:A
At equilibrium position, kx0=mg

In displaced position, U=12k(x0+y)2−mgy
=12kx20+12ky2+kx0y−mgy
Substituting kx0=mg we get,
U=12kx20+12ky2
=12kx20+12ky2+kx0y−mgy
But 12kx20 = constant say U0
∴U=U0+12ky2.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Single Correct
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A cage of mass M hangs from a light spring of force constant k. A body of mass m falls from height h inside the cage and stricks to its floor. The amplitude of oscillations of the cage will be-
_E01_061_Q01.png)
View SolutionA block of mass m is suspended through a spring of spring constant k and is in equilibrium. A sharp blow gives the block an initial downward velocity v. How far below the equilibrium position, the block comes to an instantaneous rest?
View Solution
Knowledge Check
A particle of mass m is hanging vertically by an ideal spring of force constant K . If the mass is made to oscillate vertically, its total energy is
Amaximum at the extreme positionBmaximum at the mean positionCminimum at the mean positionDsame at all positions.
The frequency f of vibrations of a mass m suspended from a spring of spring constant k is given by f=Cmxky , where C is a dimensionnless constant. The values of xandy are, respectively,
View SolutionThe frequency f of vibrations of a mass m suspended from a spring of spring constant k is given by f=Cmxky , where C is a dimensionnless constant. The values of xandy are, respectively,
View SolutionThe frequency f of vibrations of a mass m suspended from a spring of spring constant k is given by f=Cmxky , where C is a dimensionnless constant. The values of xandy are, respectively,
View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
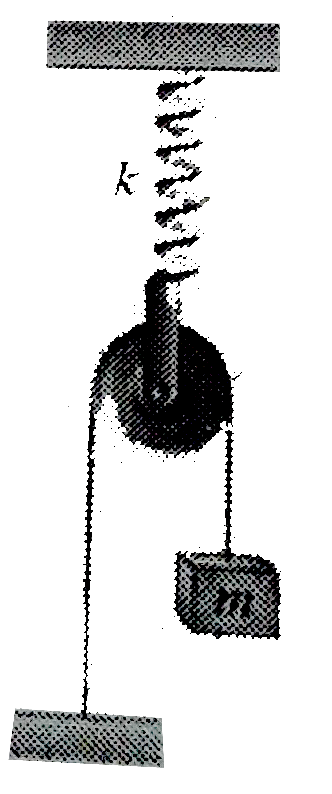
View SolutionAs shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be
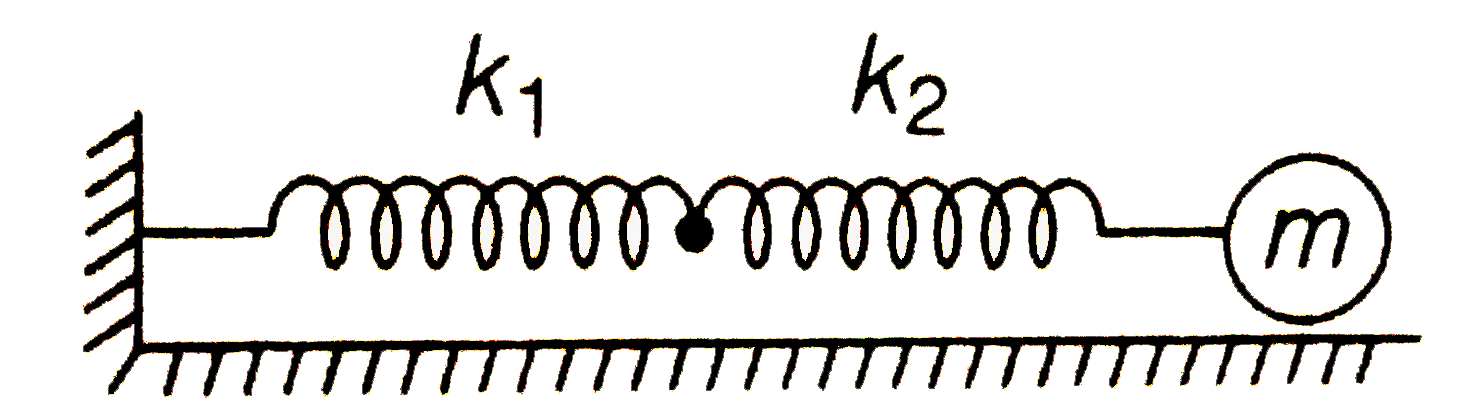
View SolutionA block of mass 4 kg hangs from a spring constant k=400Nm. The block is pulled down through 15 cm below and released. What is its kinetic energy when the block is 10 above the equilibrium position.?
View SolutionThe gravitational potential energy at a body of mass m at a distance r from the centre of the earth is U. What is the weight of the body at this distance ?
View Solution
