A particle of mass m is hanging vertically by an ideal spring of force constant K . If the mass is made to oscillate vertically, its total energy is
maximum at the extreme position
maximum at the mean position
minimum at the mean position
same at all positions.
The correct Answer is:D
The block executes SHM. In SHM, the total energy remains constant at all positions.
Topper's Solved these Questions
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Higher Order Thinking Skills
8 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Exemplar Problems
9 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
- PHYSICAL WORLDBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason
10 Videos
Similar Questions
A particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
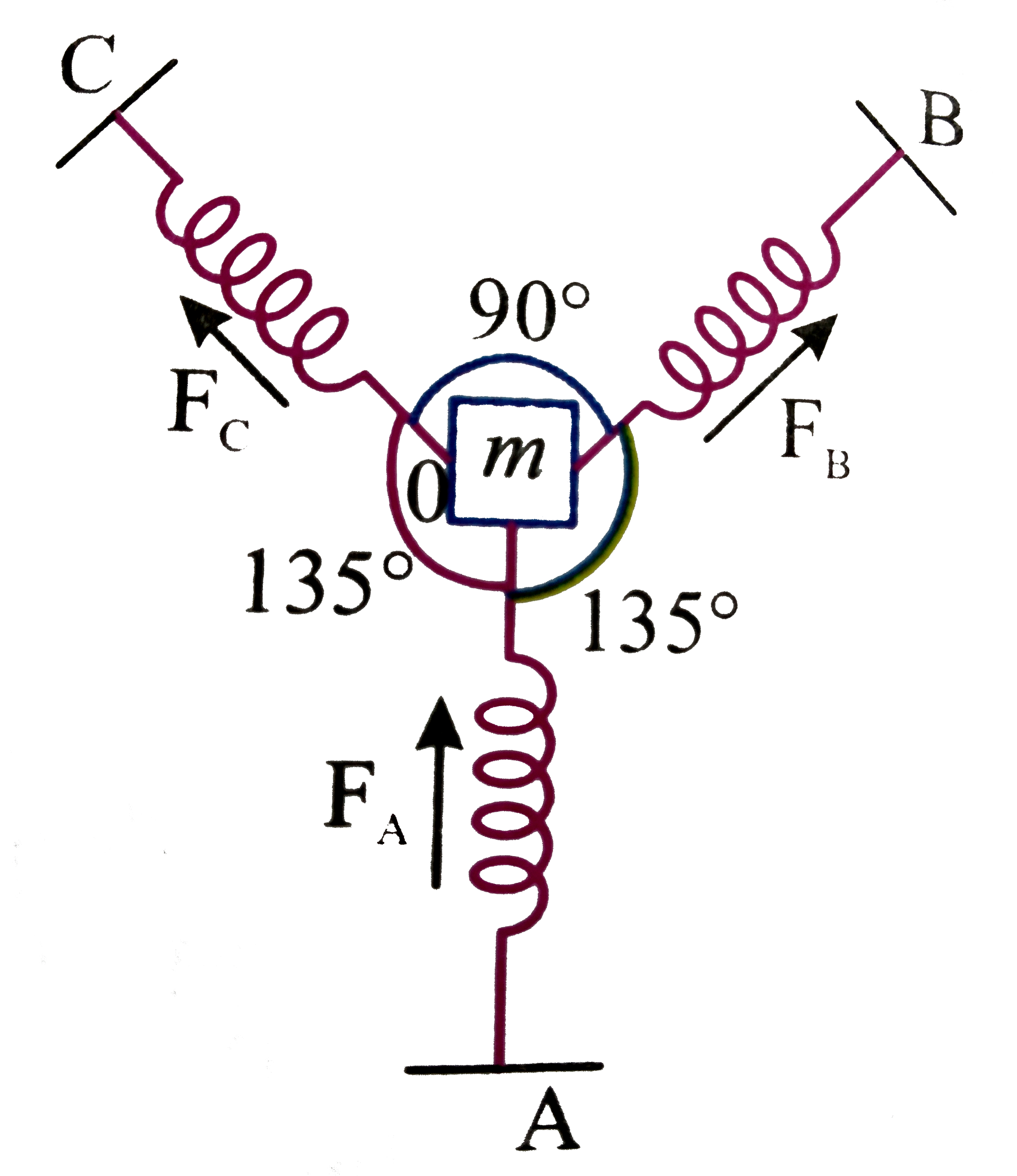
View SolutionA particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
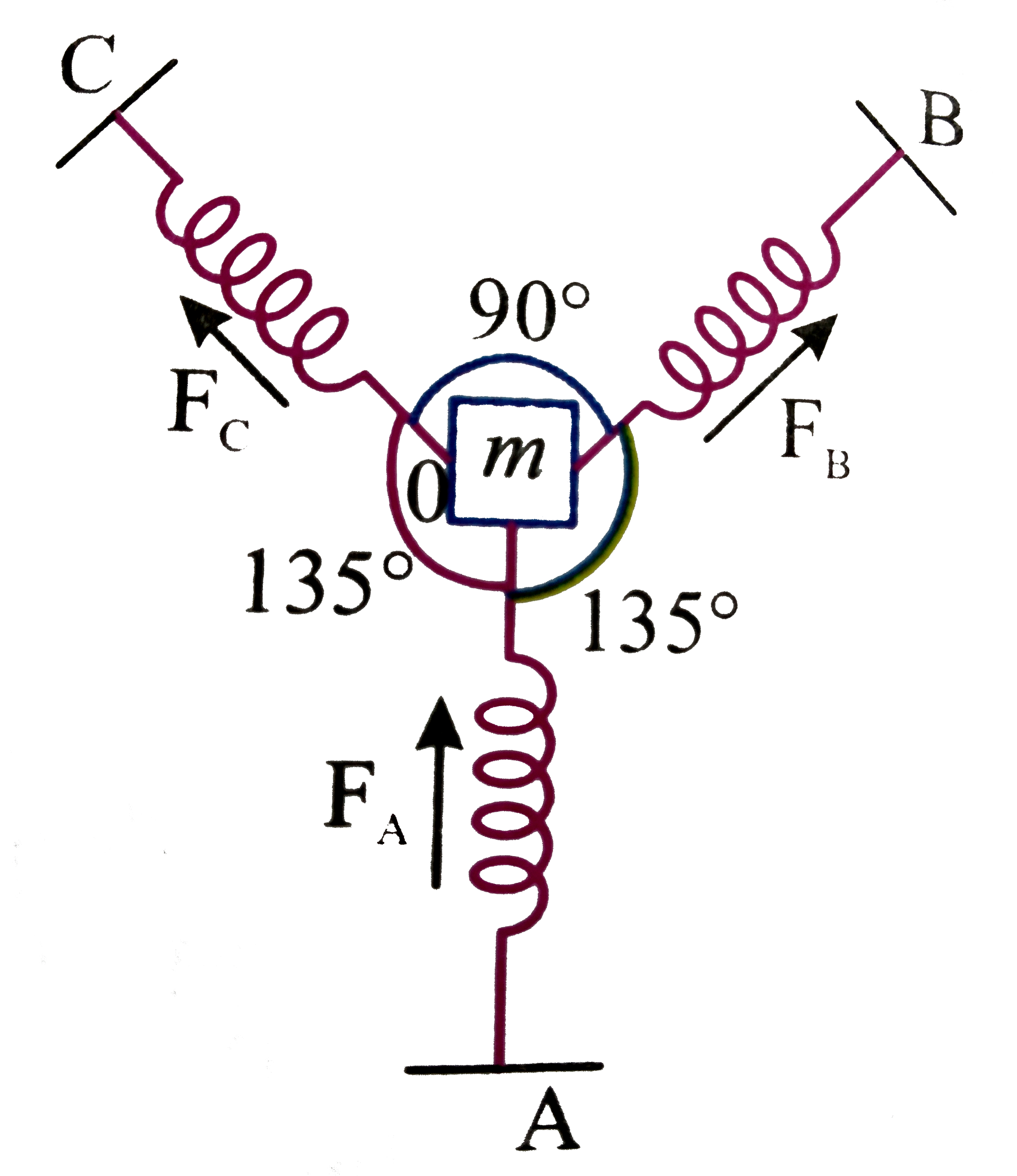
View SolutionA block of mass 'm' is hanging from a massless spring of spring constant K. It is in equilibrium under the influence of gravitational force. Another particle of same mass 'm' moving upwards with velocity ao hits the block and sticks to it. For the subsequent motion, choose the incorrect statements:

View SolutionA particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
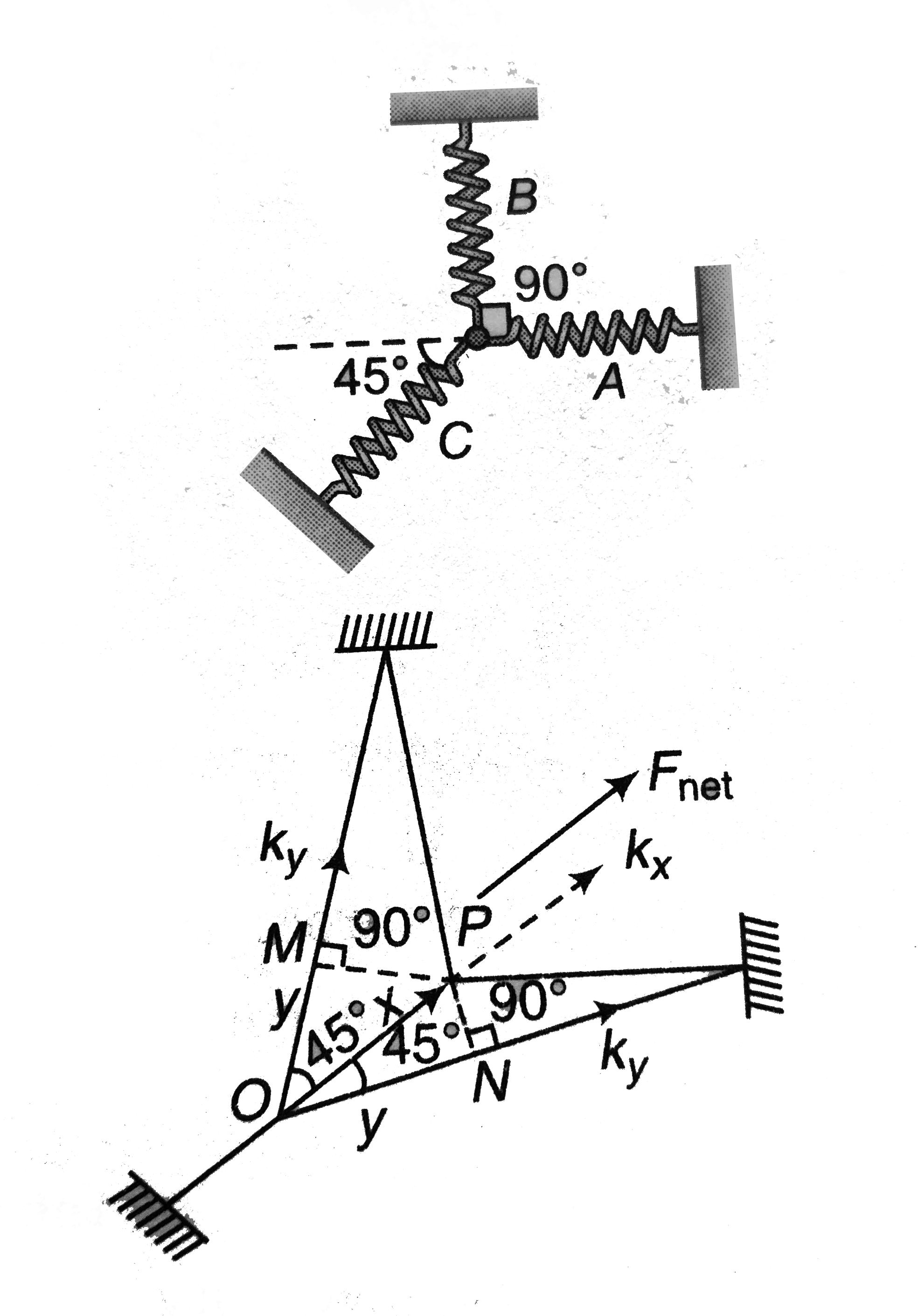 .
.
View SolutionIn the figure shown, PQ is a uniform sphere of mass M and radius R hinged at point P , with PQ as horizontal diameter. QT is a uniform horizontal rod of mass M and length 2R rigidly attached to the sphere at Q, supported by a vertical spring of spring constant k. If the system is in equilibrium, then the potential energy stored in the spring is
View SolutionWhen a particle of mass m is attached to a vertical spring of spring constant k and released, its motion is described by y(t)=y0sin2ωt, where 'y' is measured from the lower end of unstretched spring. Then ω is :
View SolutionA cage of mass M hangs from a light spring of force constant k. A body of mass m falls from height h inside the cage and stricks to its floor. The amplitude of oscillations of the cage will be-
_E01_061_Q01.png)
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
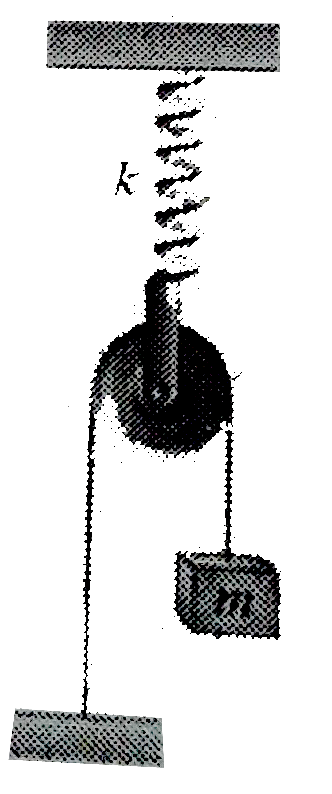
View SolutionFigure shows a system consisting of a massles pulley, a spring of force constant k and a block of mass m. If the block is sligthtly displaced vertically down from its equilibrium and released, find the period of its vertical oscillation in cases (a) and (b).

View Solution
