In the figure shown, PQ is a uniform sphere of mass M and radius R hinged at point P , with PQ as horizontal diameter. QT is a uniform horizontal rod of mass M and length 2R rigidly attached to the sphere at Q, supported by a vertical spring of spring constant k. If the system is in equilibrium, then the potential energy stored in the spring is
+MgR
MgR2
12K(R2)
M2g22k
The correct Answer is:D
To solve the problem, we need to find the potential energy stored in the spring when the system is in equilibrium. Let's break down the solution step by step.
Step 1: Understand the System
We have a uniform sphere (PQ) of mass M and radius R hinged at point P. There is a horizontal rod (QT) of mass M and length 2R attached to the sphere at point Q. The system is supported by a vertical spring with spring constant k.
Step 2: Determine the Forces Acting on the System
In equilibrium, the downward gravitational force acting on the system must be balanced by the upward force exerted by the spring. The total weight of the system can be calculated as:
Total Weight=Weight of Sphere+Weight of Rod=Mg+Mg=2Mg
Step 3: Calculate the Moment about the Hinge Point
The center of mass of the sphere is at a distance R from the hinge point P, and the center of mass of the rod is at a distance R from the hinge point (since it is uniformly distributed along its length). Therefore, the total moment about point P due to the weights is:
Moment due to Sphere=Mg⋅R
Moment due to Rod=Mg⋅(R+R)=2Mg⋅R
Thus, the total moment is:
Total Moment=MgR+2MgR=3MgR
Step 4: Relate the Spring Force to the Displacement
Let x be the displacement of the spring from its natural length. The force exerted by the spring is given by Hooke's Law:
Fspring=kx
In equilibrium, this spring force must balance the total weight:
kx=3Mg
Step 5: Solve for x
From the equation kx=3Mg, we can solve for x:
x=3Mgk
Step 6: Calculate the Potential Energy Stored in the Spring
The potential energy U stored in the spring is given by the formula:
U=12kx2
Substituting the value of x:
U=12k(3Mgk)2
U=12k⋅9M2g2k2
U=9M2g22k
Final Answer
Thus, the potential energy stored in the spring is:
U=9M2g22k
We have a uniform sphere (PQ) of mass M and radius R hinged at point P. There is a horizontal rod (QT) of mass M and length 2R attached to the sphere at point Q. The system is supported by a vertical spring with spring constant k.
In equilibrium, the downward gravitational force acting on the system must be balanced by the upward force exerted by the spring. The total weight of the system can be calculated as:
Total Weight=Weight of Sphere+Weight of Rod=Mg+Mg=2Mg
The center of mass of the sphere is at a distance R from the hinge point P, and the center of mass of the rod is at a distance R from the hinge point (since it is uniformly distributed along its length). Therefore, the total moment about point P due to the weights is:
Moment due to Sphere=Mg⋅R
Moment due to Rod=Mg⋅(R+R)=2Mg⋅R
Thus, the total moment is:
Total Moment=MgR+2MgR=3MgR
Let x be the displacement of the spring from its natural length. The force exerted by the spring is given by Hooke's Law:
Fspring=kx
In equilibrium, this spring force must balance the total weight:
kx=3Mg
From the equation kx=3Mg, we can solve for x:
x=3Mgk
The potential energy U stored in the spring is given by the formula:
U=12kx2
Substituting the value of x:
U=12k(3Mgk)2
U=12k⋅9M2g2k2
U=9M2g22k
Thus, the potential energy stored in the spring is:
U=9M2g22k
Similar Questions
A rod mass (M) hinged at (O) is kept in equilibrium with a spring of stiffness (k) as shown in figure. The potential energy stored in the spring is .

View Solution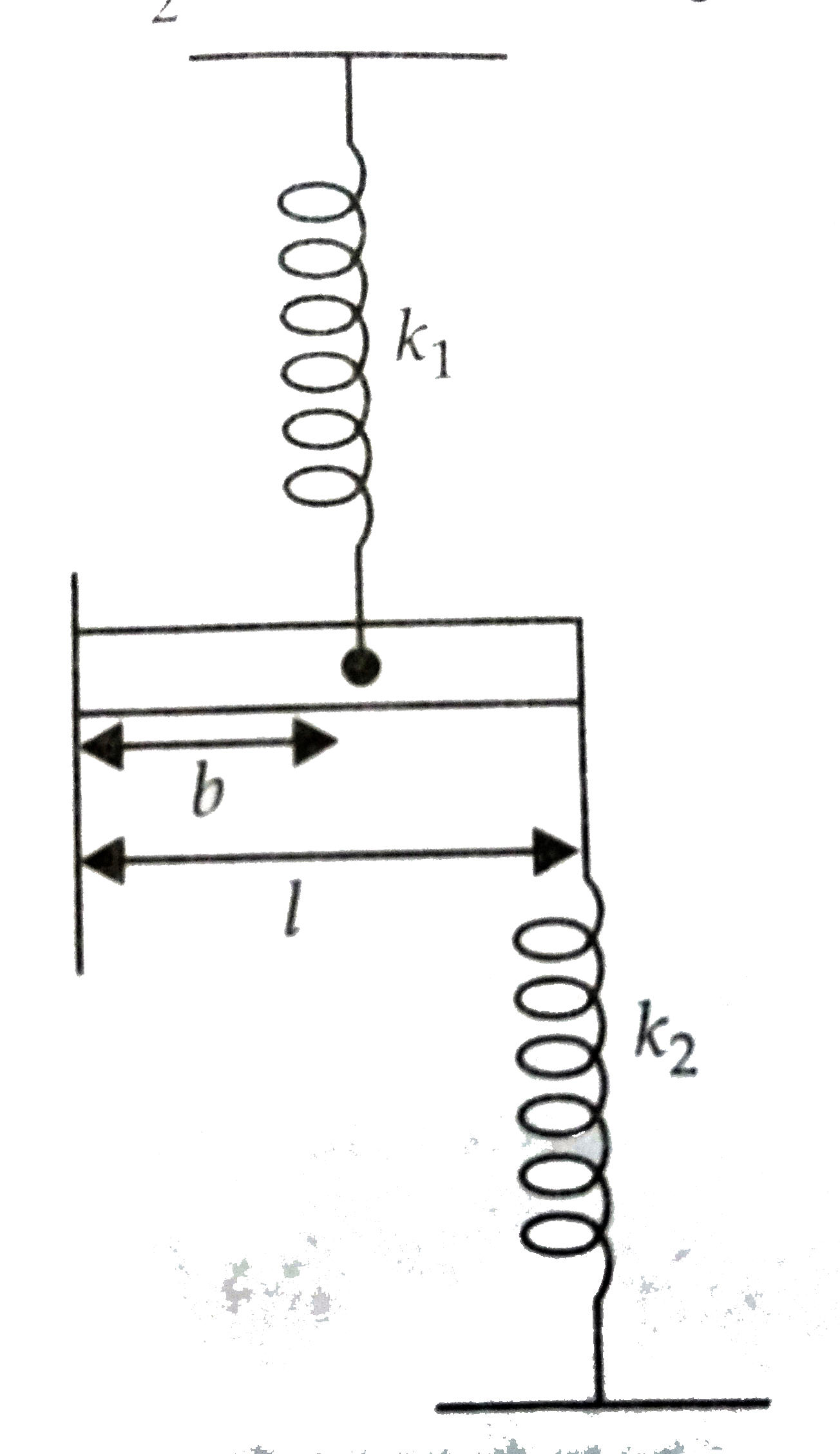
A rod of mass m and length l is connected by two spring of spring constants k1andk2, so that it is horizontal at equilibrium. What is the natural frequency of the system?
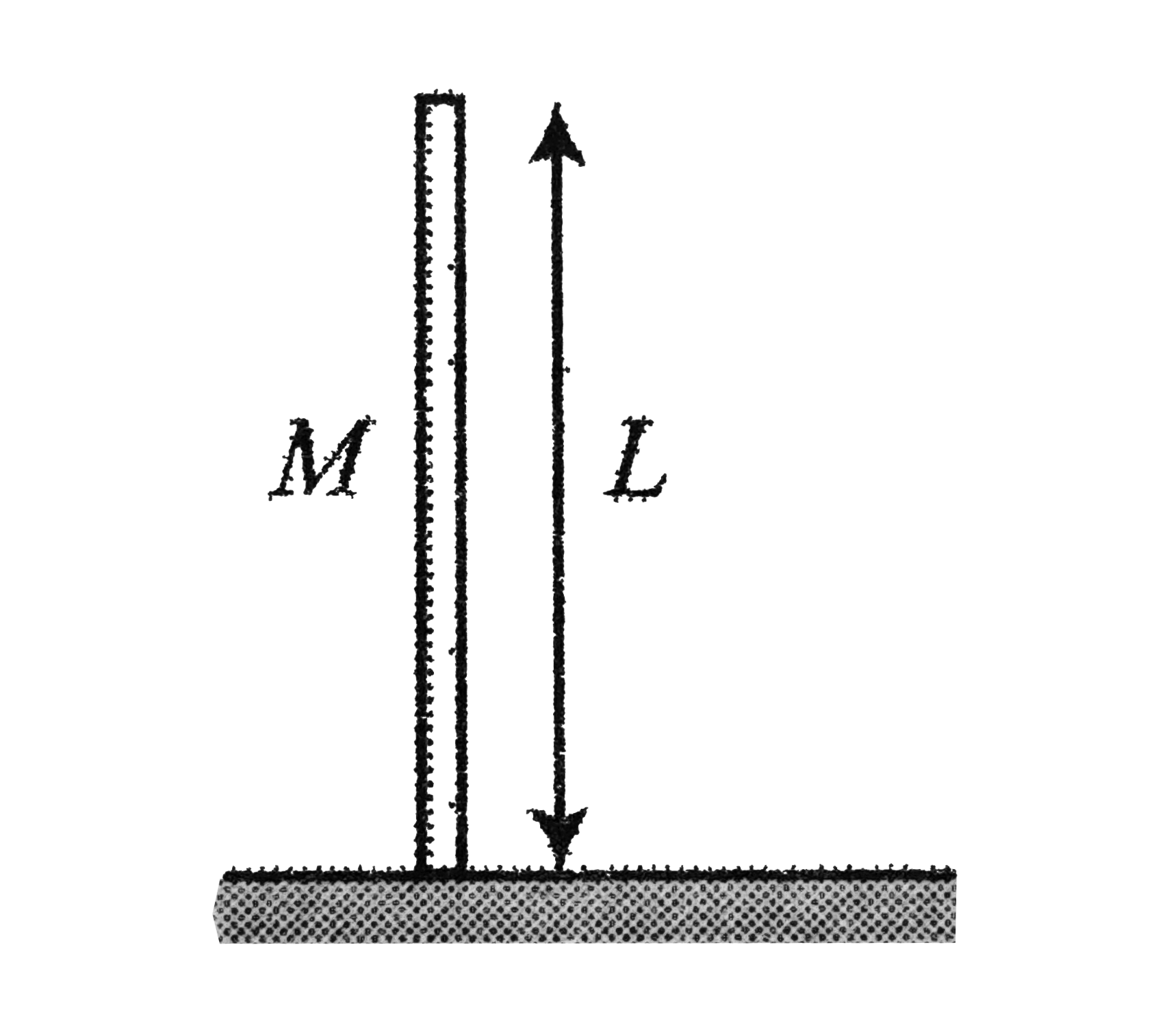
View SolutionA uniform rod of mass M and length L is held vertically upright on a horizontal surface as shown in figure. Assuming zero potential energy at the base of the rod, determine the potential energy of the rod.
View SolutionA uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the intial angular acceleration of the rod is

View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionA spring, placed horizontally on a rough surface is compressed by a block of mass m, placed on the same surface so as to store maximum energy in the spring. If the coefficient of friction between the block and the surface is μ, the potential energy stored in the spring is
View SolutionThree solid sphere of mass M and radius R are placed in contact as shown in figure. Find the potential energy of the system ?
View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in the figure. When string is cut, the initial angular accleration of the rod is.

View SolutionA block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
View Solution

