Three solid sphere of mass M and radius R are placed in contact as shown in figure. Find the potential energy of the system ?
To find the potential energy of the system of three solid spheres of mass M and radius R that are placed in contact, we can follow these steps:
Step 1: Understand the Configuration
The three spheres are in contact with each other, forming an equilateral triangle. The distance between the centers of any two spheres is equal to 2R (since the radius of each sphere is R).
Step 2: Use the Formula for Gravitational Potential Energy
The gravitational potential energy U between two masses m1 and m2 separated by a distance r is given by:
U=−Gm1m2r
In our case, since each sphere has mass M, the potential energy between any two spheres will be:
Uij=−GM22R
where i and j denote any two spheres.
Step 3: Calculate the Total Potential Energy
Since there are three pairs of spheres (1-2, 2-3, and 1-3), we can calculate the total potential energy of the system by summing the potential energies of each pair:
Utotal=U12+U23+U13
Substituting the potential energy for each pair:
Utotal=−GM22R+−GM22R+−GM22R
This simplifies to:
Utotal=−3GM22R
Step 4: Final Result
Thus, the total potential energy of the system of three solid spheres is:
U=−3GM22R
The three spheres are in contact with each other, forming an equilateral triangle. The distance between the centers of any two spheres is equal to 2R (since the radius of each sphere is R).
The gravitational potential energy U between two masses m1 and m2 separated by a distance r is given by:
U=−Gm1m2r
In our case, since each sphere has mass M, the potential energy between any two spheres will be:
Uij=−GM22R
where i and j denote any two spheres.
Since there are three pairs of spheres (1-2, 2-3, and 1-3), we can calculate the total potential energy of the system by summing the potential energies of each pair:
Utotal=U12+U23+U13
Substituting the potential energy for each pair:
Utotal=−GM22R+−GM22R+−GM22R
This simplifies to:
Utotal=−3GM22R
Thus, the total potential energy of the system of three solid spheres is:
U=−3GM22R
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - BOX-1
3 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - BOX-2
13 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 5 B (Previous Year Questions)
9 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
Similar Questions
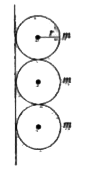
Three identical rings of masses m each and radius r are kept in contact as shown in Fig. Find the moment of inertia of the system about a common tangent.
View SolutionA solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is

View Solution
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
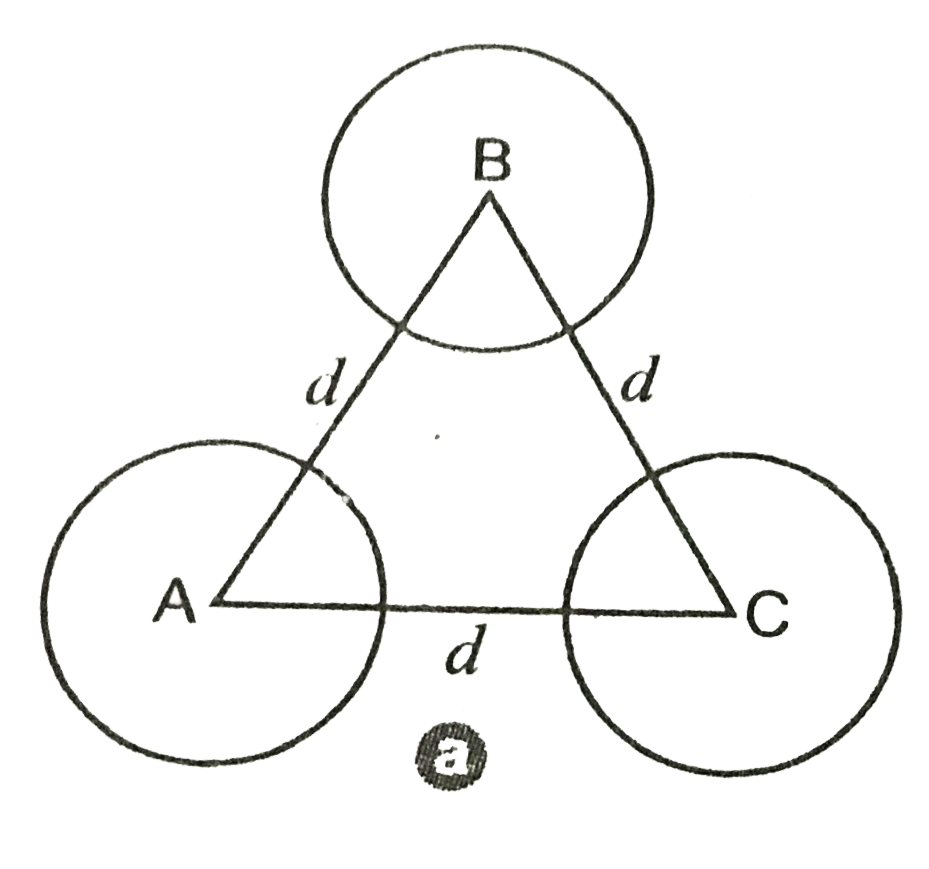
View SolutionThree solid spheres each of mass m and radius R are released from the position shown in Fig. What is the speed of any one sphere at the time of collision?
View SolutionA solid sphere of mass M and radius R is in pure rolling as shown in figure. The angular momentum of the sphere about the origin is (linear velocity of centre of mass is v0, in positive x-direction)
View SolutionThree charges are placed along x-axis at x = - a x = 0 and x = a as shown in the figure. The potential energy of the system is

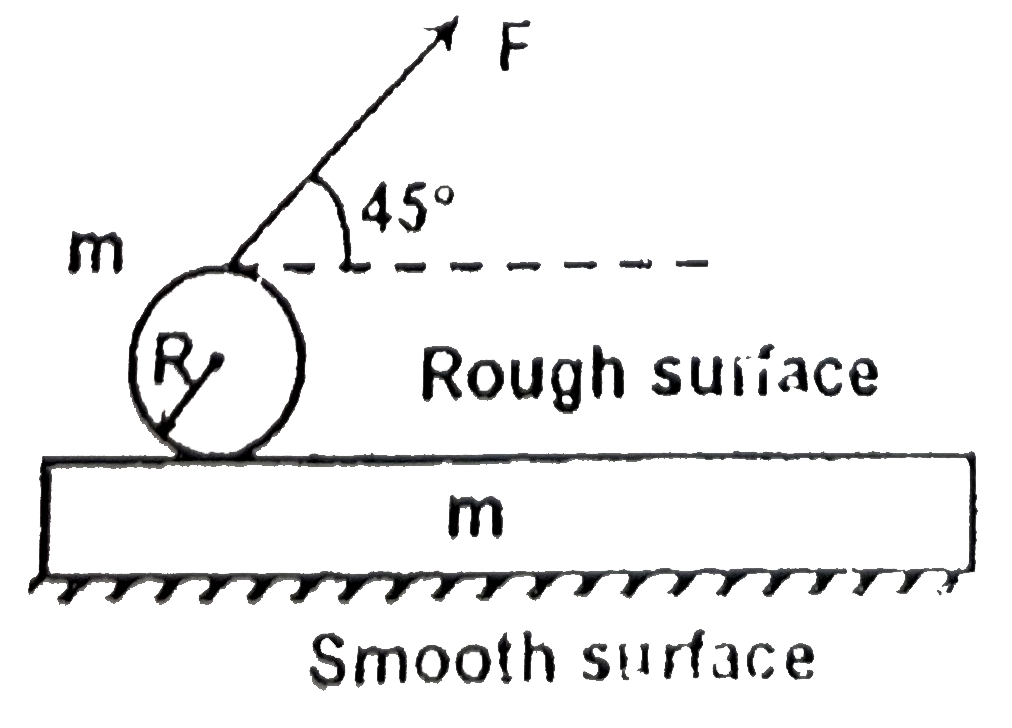
View SolutionA plank of mass m is placed on a smooth surface. Now, a uniform solid sphere of equal mass m and radius R is placed on the plank as shown in the figure. A force F is applied at topmost point of the sphere at an angle of 45∘ to the horizontal. Surface between the plank and the sphere is extremely rough so that there is no slip between the plank and the sphere. The force of firction acting between the plank and the sphere is Fk√2. Find the value of k.
View SolutionFour rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY' will be

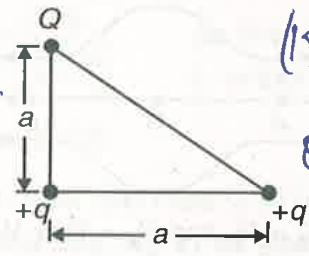
View SolutionThree charges +q , +q, and Q are placed at the comers of a right angled isosceles triangle as shown in the figure. If the net potential energy of the system is zero then value of Q is
View SolutionA system of three charges are placed as shown in the figure :
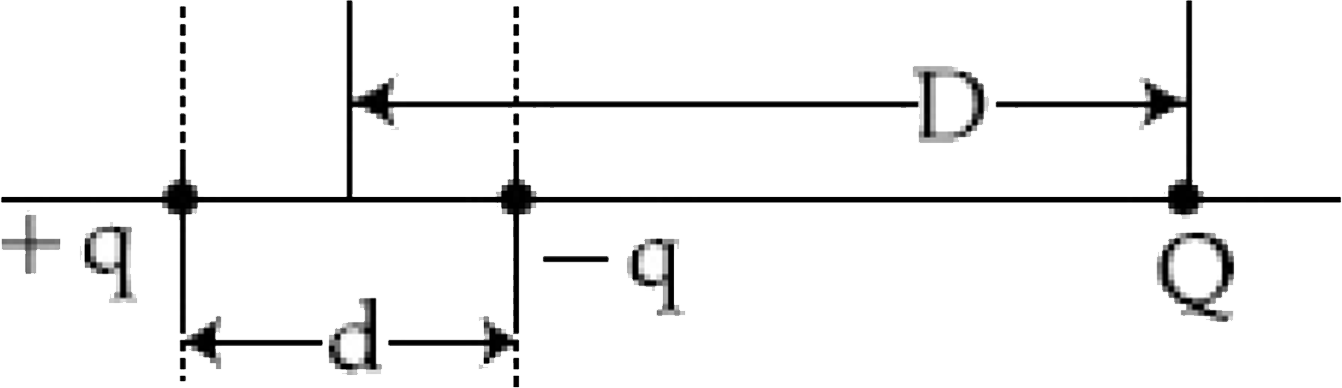
If D>>d, the potential energy of the system is best given by :
View Solution
