A block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
(a)v√m/2k
(b)v√m/k
(c)v√m/4k
(d)mv2/4k
The correct Answer is:A
To solve the problem step by step, we will use the principle of conservation of energy.
Step 1: Understand the Initial Conditions
The block of mass m is moving with an initial speed v on a frictionless surface. As it compresses the spring, it loses kinetic energy and gains potential energy.
Step 2: Write the Expression for Kinetic Energy
The initial kinetic energy (KE) of the block is given by:
KE=12mv2
Step 3: Write the Expression for Potential Energy
The potential energy (PE) stored in the spring when compressed by a distance x is given by:
PE=12kx2
Step 4: Set Kinetic Energy Equal to Potential Energy
According to the problem, at the instant when the kinetic energy of the block is equal to the potential energy of the spring, we can write:
12mv2=12kx2
Step 5: Simplify the Equation
We can eliminate the 12 from both sides:
mv2=kx2
Step 6: Solve for x
Rearranging the equation to solve for x:
x2=mv2k
Taking the square root of both sides gives:
x=√mv2k
Step 7: Final Expression for Compression
Thus, the distance x at which the spring is compressed when the kinetic energy equals the potential energy is:
x=v√mk
Conclusion
The distance the spring is compressed when the kinetic energy of the block equals the potential energy of the spring is:
x=v√mk
The block of mass m is moving with an initial speed v on a frictionless surface. As it compresses the spring, it loses kinetic energy and gains potential energy.
The initial kinetic energy (KE) of the block is given by:
KE=12mv2
The potential energy (PE) stored in the spring when compressed by a distance x is given by:
PE=12kx2
According to the problem, at the instant when the kinetic energy of the block is equal to the potential energy of the spring, we can write:
12mv2=12kx2
We can eliminate the 12 from both sides:
mv2=kx2
Rearranging the equation to solve for x:
x2=mv2k
Taking the square root of both sides gives:
x=√mv2k
Thus, the distance x at which the spring is compressed when the kinetic energy equals the potential energy is:
x=v√mk
The distance the spring is compressed when the kinetic energy of the block equals the potential energy of the spring is:
x=v√mk
Topper's Solved these Questions
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:Level - 1 PARAGRAPH QUESTIONS
Explore 3 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:LEVEL - 2
Explore 48 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:LEVEL - 0 - LONG ANSWER TYPE
Explore 5 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE Advanced (Archive)
Explore 89 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
Similar Questions
The potential energy of a weight less spring compressed by a distance a is proportional to
View SolutionIn figure, a block A of mass 2kg is moving to the right with a speed 5m/s on a horizontal frictionless surface. Another block B of mass 3kg a massless spring of spring constant 222N/m attached to it, is moving to the left on the same surface and with a speed 2m/s . Let us take the direction to the right as the positive X− direction. At some instant, block A collides with the spring attached to block B. At some other instant , the spring has maximum compression and then, finally, blocks move with their final velocities. Assuming that (i) the spring force is conservative and so there is no conversion of kinetic energy to internal energy and (ii), no sound is made when block A hits the spring, answer the following questions.
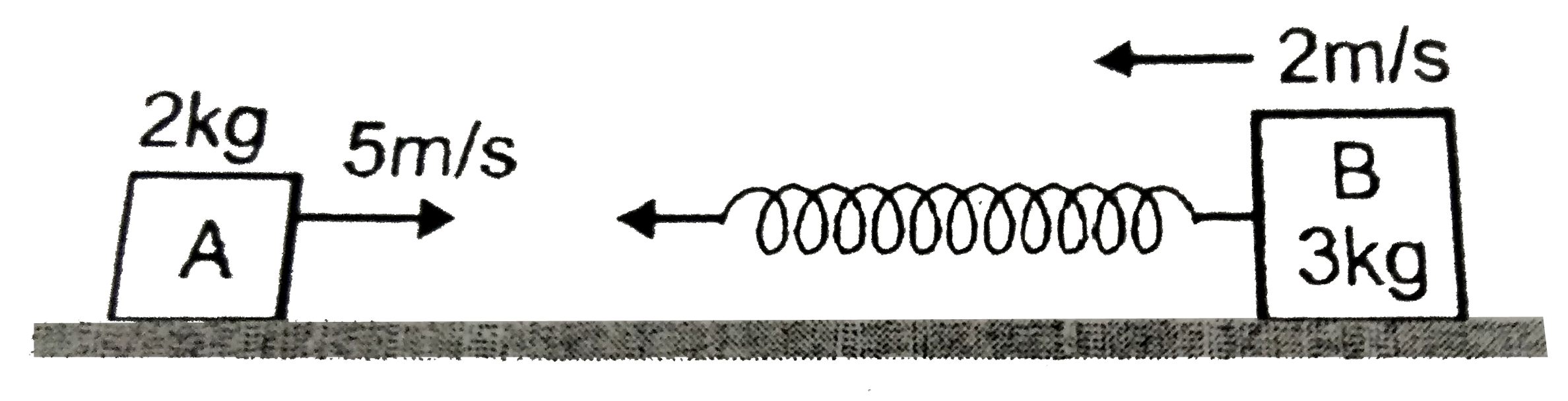
When the blocks are yet to attain their final velocities, in this situation at any instant when block A is moving with a velocity 4ˆim/s , velocity of block B will then be :
View SolutionIn figure, a block A of mass 2kg is moving to the right with a speed 5m/s on a horizontal frictionless surface. Another block B of mass 3kg a massless spring of spring constant 222N/m attached to it, is moving to the left on the same surface and with a speed 2m/s . Let us take the direction to the right as the positive X− direction. At some instant, block A collides with the spring attached to block B. At some other instant , the spring has maximum compression and then, finally, blocks move with their final velocities. Assuming that (i) the spring force is conservative and so there is no conversion of kinetic energy to internal energy and (ii), no sound is made when block A hits the spring, answer the following questions.
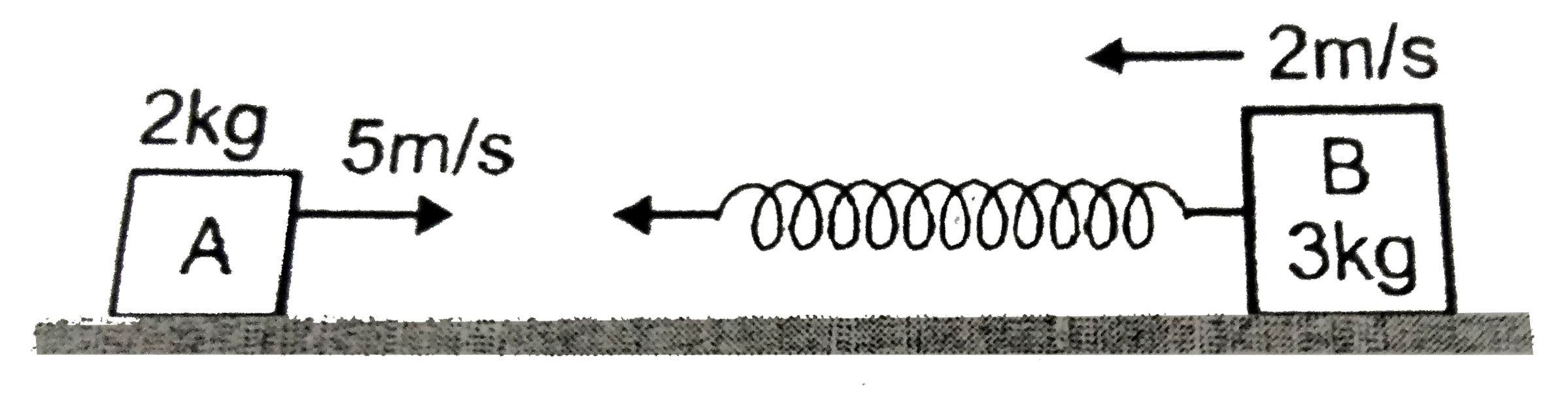
In the collision process, while the spring is getting compressed :
View SolutionIn figure, a block A of mass 2kg is moving to the right with a speed 5m/s on a horizontal frictionless surface. Another block B of mass 3kg a massless spring of spring constant 222N/m attached to it, is moving to the left on the same surface and with a speed 2m/s . Let us take the direction to the right as the positive X− direction. At some instant, block A collides with the spring attached to block B. At some other instant , the spring has maximum compression and then, finally, blocks move with their final velocities. Assuming that (i) the spring force is conservative and so there is no conversion of kinetic energy to internal energy and (ii), no sound is made when block A hits the spring, answer the following questions.

Maximum compression of the spring in the collision will be nearly
View SolutionIn figure, a block A of mass 2kg is moving to the right with a speed 5m/s on a horizontal frictionless surface. Another block B of mass 3kg a massless spring of spring constant 222N/m attached to it, is moving to the left on the same surface and with a speed 2m/s . Let us take the direction to the right as the positive X− direction. At some instant, block A collides with the spring attached to block B. At some other instant , the spring has maximum compression and then, finally, blocks move with their final velocities. Assuming that (i) the spring force is conservative and so there is no conversion of kinetic energy to internal energy and (ii), no sound is made when block A hits the spring, answer the following questions.
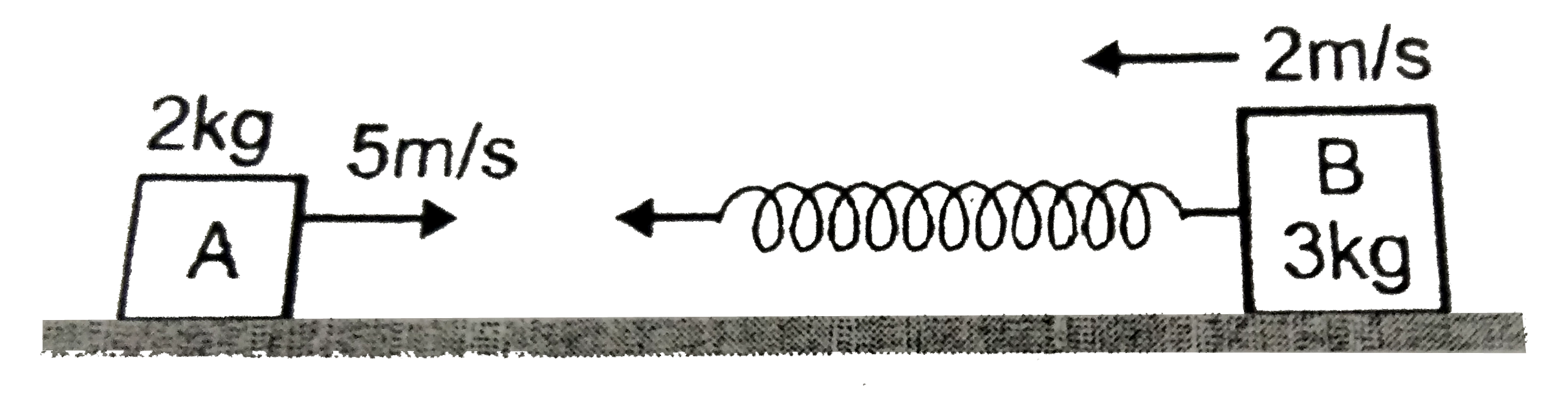
Velocity of centre of mass of the system of blocks A and B, before collision is :
View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is

View SolutionA compressed spring of an air gun has kinetic energy.
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)

View SolutionA bullet of mass m embeds itself in a block of mass M resting on a smooth horizontal surface, attached to a spring of force constant k. If the initial speed of the bullet is v0 along horizontal, find (a) the maximum compression of the spring and (b) the time for the bullet - block system to come to rest.
View Solution