A projectile takes off with an initial velocity of 10m/s at an angle of elevation of 45∘. It is just able to clear two hurdles of height 2 m each, separated from each other by a distance d. Calculate d. At what distance from the point of projection is the first hurdle placed? Take g=10m/s2.
The correct Answer is:B, D
To solve the problem, we need to find the distance d between the two hurdles and the distance from the point of projection to the first hurdle.
1. Identify the given values:
- Initial velocity u=10m/s
- Angle of elevation θ=45∘
- Height of hurdles y=2m
- Acceleration due to gravity g=10m/s2
2. Resolve the initial velocity into horizontal and vertical components:
ux=ucosθ=10cos45∘=10×1√2=5√2m/s
uy=usinθ=10sin45∘=10×1√2=5√2m/s
3. Use the projectile motion equation to find the horizontal distance x when the projectile reaches the height of the hurdles:
The equation for vertical motion is given by:
y=xtanθ−gx22u2cos2θ
Substituting the known values:
2=xtan45∘−10x22×102cos245∘
Since tan45∘=1 and cos245∘=12:
2=x−10x22×100×12
Simplifying gives:
2=x−x210
4. Rearranging the equation:
x210+2−x=0
Multiplying through by 10 to eliminate the fraction:
x2−10x+20=0
5. Using the quadratic formula to solve for x:
The quadratic formula is given by:
x=−b±√b2−4ac2a
Here, a=1,b=−10,c=20:
x=10±√(−10)2−4⋅1⋅202⋅1
x=10±√100−802
x=10±√202
x=10±2√52
x=5±√5
6. Finding the distances:
- The two possible values for x are 5+√5 and 5−√5.
- The distance d between the two hurdles is:
d=(5+√5)−(5−√5)=2√5
- The distance from the point of projection to the first hurdle is:
x1=5−√5
7. Final calculations:
- Calculate d:
d≈2×2.236=4.472m≈4.47m
- Calculate x1:
x1≈5−2.236=2.764m≈2.75m
Final Answers:
- The distance d between the hurdles is approximately 4.47m.
- The distance from the point of projection to the first hurdle is approximately 2.75m.
- Initial velocity u=10m/s
- Angle of elevation θ=45∘
- Height of hurdles y=2m
- Acceleration due to gravity g=10m/s2
ux=ucosθ=10cos45∘=10×1√2=5√2m/s
uy=usinθ=10sin45∘=10×1√2=5√2m/s
The equation for vertical motion is given by:
y=xtanθ−gx22u2cos2θ
Substituting the known values:
2=xtan45∘−10x22×102cos245∘
Since tan45∘=1 and cos245∘=12:
2=x−10x22×100×12
Simplifying gives:
2=x−x210
x210+2−x=0
Multiplying through by 10 to eliminate the fraction:
x2−10x+20=0
The quadratic formula is given by:
x=−b±√b2−4ac2a
Here, a=1,b=−10,c=20:
x=10±√(−10)2−4⋅1⋅202⋅1
x=10±√100−802
x=10±√202
x=10±2√52
x=5±√5
- The two possible values for x are 5+√5 and 5−√5.
- The distance d between the two hurdles is:
d=(5+√5)−(5−√5)=2√5
- The distance from the point of projection to the first hurdle is:
x1=5−√5
- Calculate d:
d≈2×2.236=4.472m≈4.47m
- Calculate x1:
x1≈5−2.236=2.764m≈2.75m
- The distance d between the hurdles is approximately 4.47m.
- The distance from the point of projection to the first hurdle is approximately 2.75m.
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 More Than One Correct
8 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
A projectile takes off with an initial velocity of 50m//s at an angle of 37∘ with horizontal, It is just able to clear two hurdles of height 25m each, separated from each other by a distance d Calculate d.
View SolutionA particle is projected from a tower as shown in figure, then find the distance from the foot of the tower where it will strike the ground. (g=10m/s2)
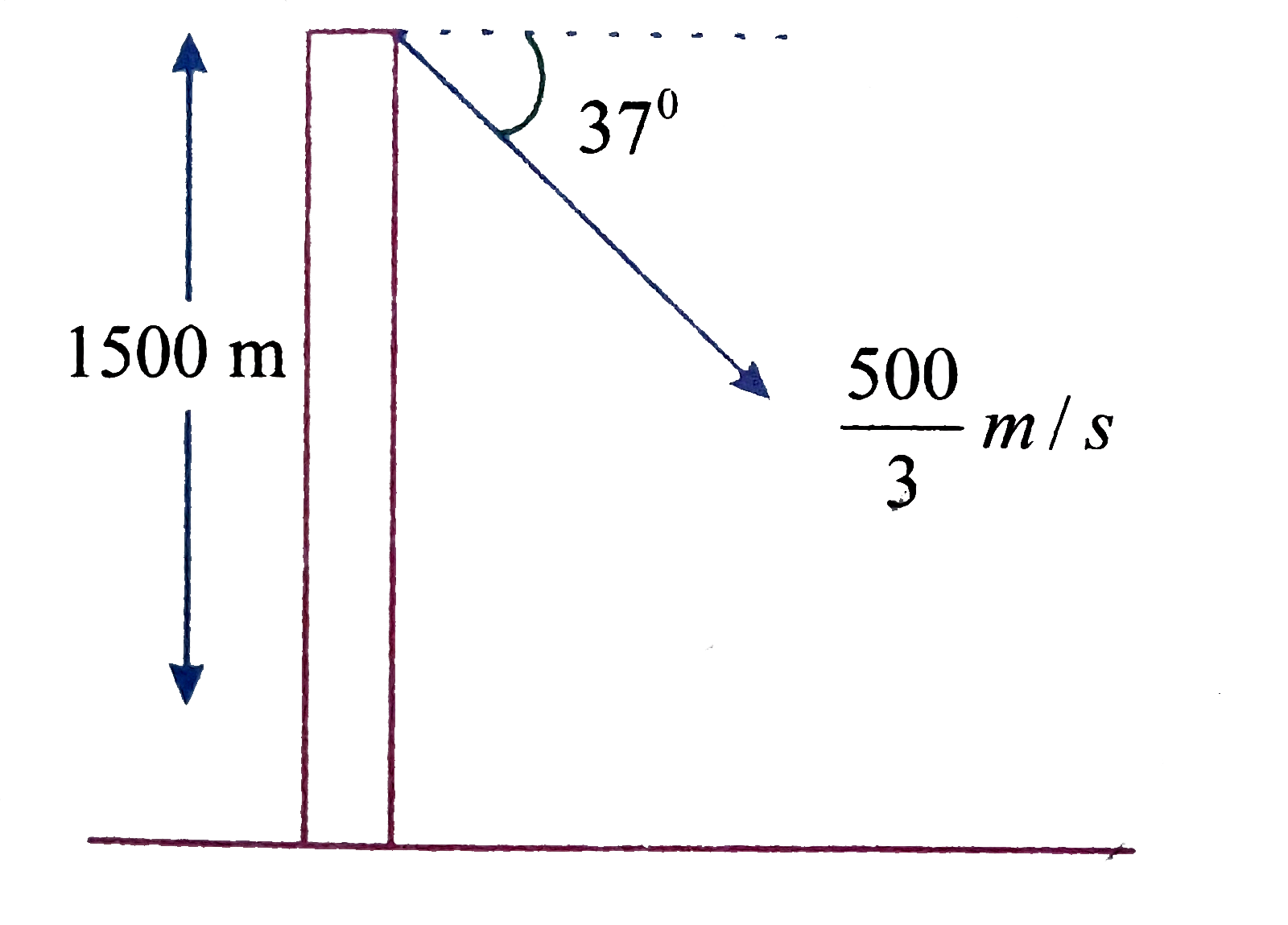
View Solution
Knowledge Check
A ball is thrown from the top of a tower with an initial velocity of 10m/s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
A5 mB20 mC15 mD10 m
A particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA particle A is projected from the ground with an initial velocity of 10m/s at an angle of 60∘ with horizontal. From what height should an another particle B be projected horizontally with velocity 5m/s so that both the particles collide in ground at point C if both are projected simultaneously g=10m/s2.
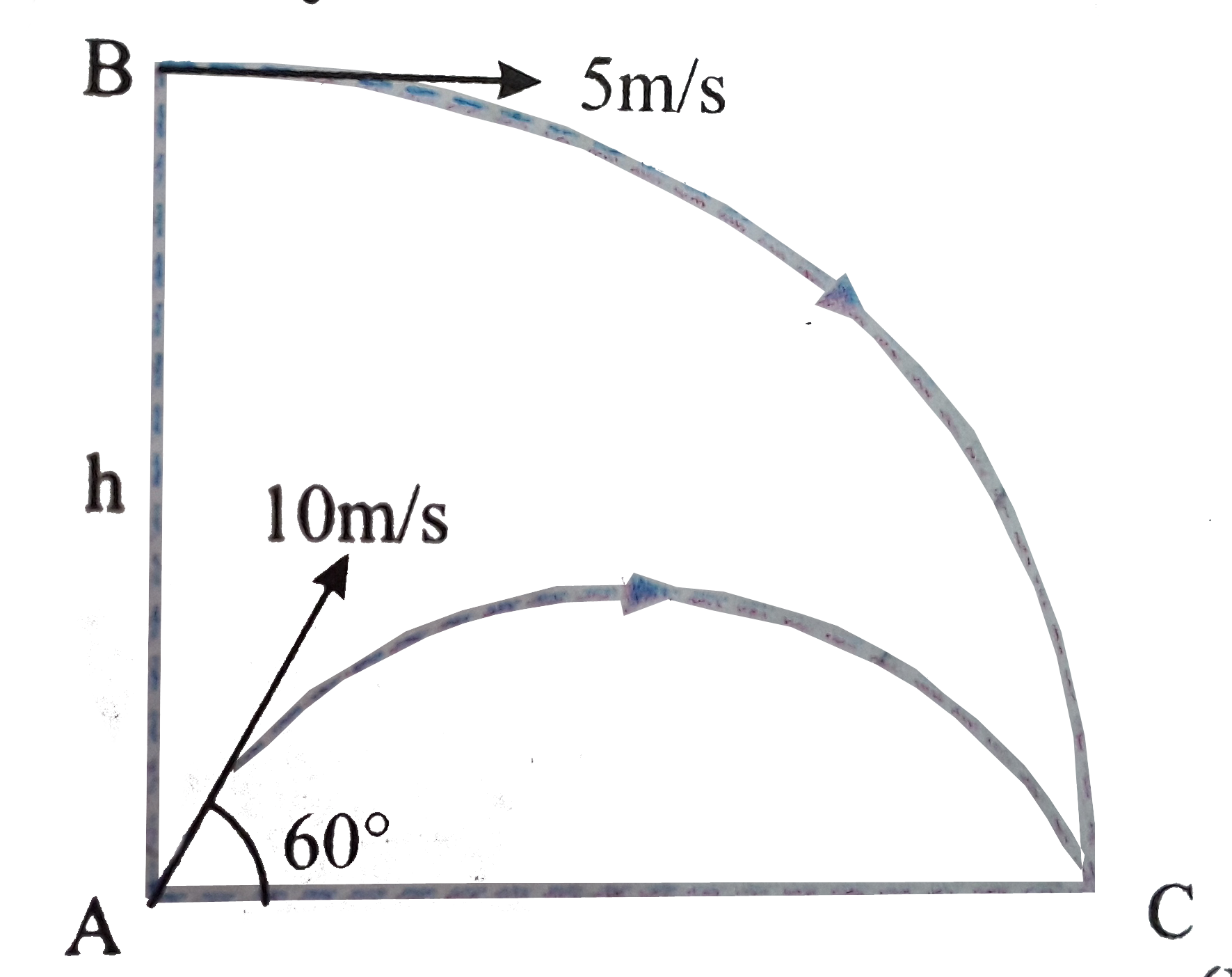
View SolutionA particle A is projected with an initial velocity of 60m/s at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a)the angle of projection α of particle B, (b) time when the collision takes place and (c) the distance of P from A, where collision occurs. (g=10m/s2)
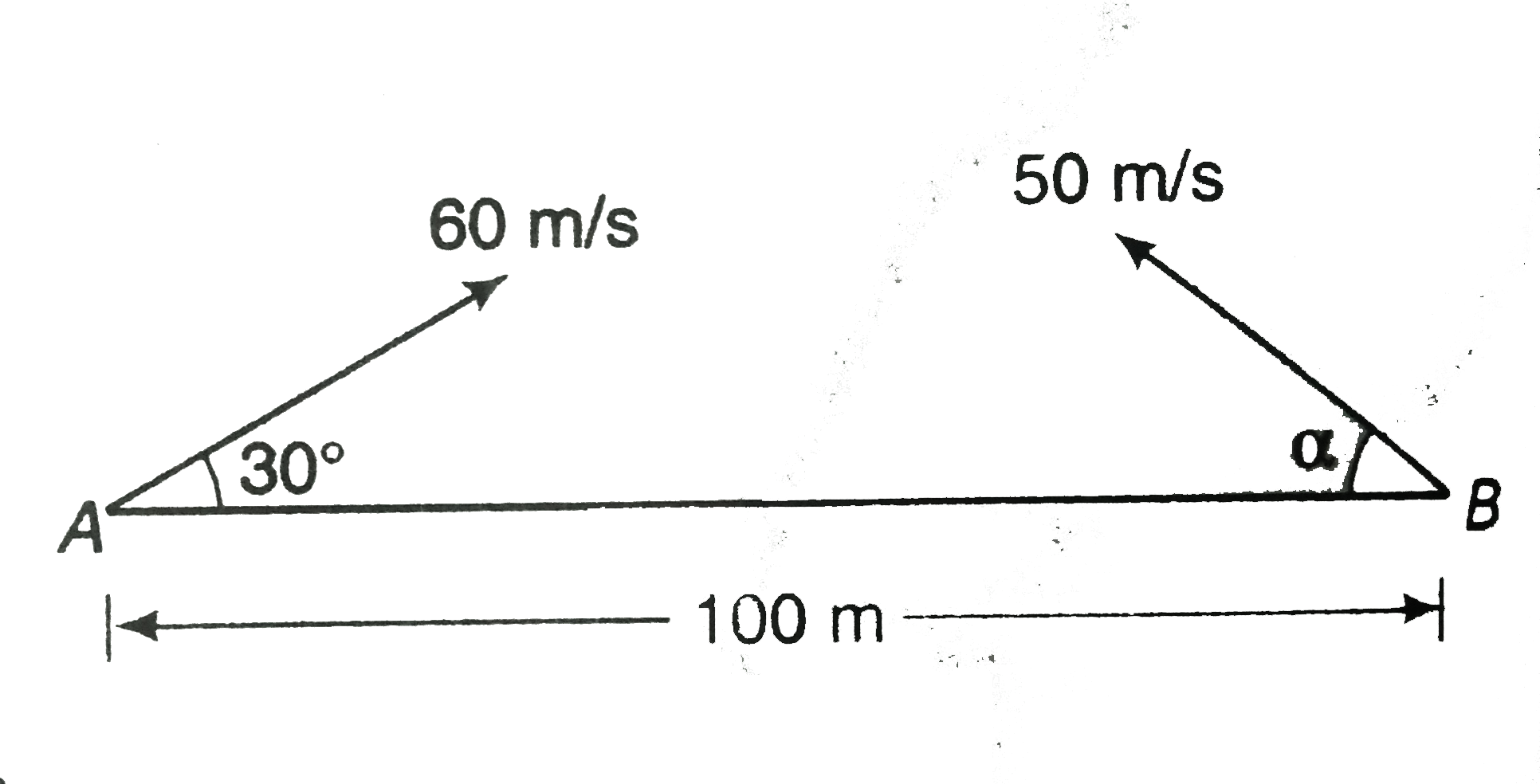
View SolutionA particle is projected with velocity of 10ms at an angle of 15° with horizontal.The horizontal range will be(g=10ms2)
View SolutionA ball is projected vertically up with speed 20 m/s. Take g=10m/s2
View SolutionA body is projected with an initial Velocity 20 m/s at 60° to the horizontal. Its initial velocity vector is- (g=10 m/s2)
View SolutionA ball is thrown from the top of a tower with an intial velocity of 10 m//s at an angle 37∘ above the horizontal, hits the ground at a distance 16 m from the base of tower. Calculate height of tower. [g=10m/s2]
View Solution