A particle is projected from point O on the ground with velocity u=5(√5)m/s at angle α=tan−1(0.5). It strikes at a point C on a fixed smooth plane AB having inclination of 37∘ with horizontal as shown in figure. If the particle does not rebound, calculate.
(a) coordinates of point C in reference to coordinate system as shown in the figure.
(b) maximum height from the ground to which the particles rises. (g=10m/s2)

The correct Answer is:A, B, D
(a) Let, (x,y) be the coordinates of point C.

x=OD=OA+AD
∴x=103+ycot37∘=10+4y3 ………(i)
As point C lies on the trajectory of a parabola,
we have
y=xtanα−(gx)2(2u)2(1+tan2α).........(ii)
Given that , tanα=0.5=12
Solving Eqs. (i) and (ii), we get x = 5m and y = 1.25m.
Hence, the coordinates of point C are (5m, 1.25m).
(b) Let vy be the vertical component of velocity of
the particle just before collision at C.

Using vy=uy+ayt,wehave
vy=usinα−g(x/ucosα)⟨'t=x/ucosα)
=5√5√5−10×55(√5)×2/(√5)=0
Thus, at C, the particle has only horizontal
component of velocity
vx=ucosα=5(√5)×(2/(√5))=10m/s
Given, that the particle does not rebound after collision. So, the normal component of velocity
(normal to the plane AB) becomes zero. Now,
the particle slides up the plane due to tangential
component vxcos37∘=(10)(45)=8m/s
Let h be the further height raised by the particle.
Then,
mgh=12m(8)2orh=3.2m
Height of the particle from the ground =y+h
∴H=1.25+3.2=4.45m.
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 More Than One Correct
8 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
A particle is projected form point O on the ground with velocity u=√5m/s at angle α=tan−1(0.5). It strikes at a point C on a fixed smooth plane AB having inclination of 37∘ with horizontal as shown is Fig. If the particle does not rebound , calculate .
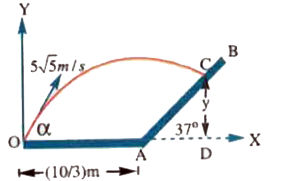
(a) coordinates of point C in reference t coordinate system as shown in the figure .
(b) maximum heing from the ground to which the particle reises. (g=10m/s2)
View SolutionA ball is projected from the point O with velocity 20 m/s at an angle of 60∘ with horizontal as shown in figure. At highest point of its trajectory it strikes a smooth plane of inclination 30∘ at point A. The collision is perfectly inelastic. The maximum height from the ground attained by the ball is (g=10m/s2)

View SolutionA particle is projected from a point A with velocity √2u an angle of 45∘ with horizontal as shown in figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is

View SolutionA particle is projected along an inclined plane as shown in figure. What is the speed of the particle when it collides at point A ? (g=10ms2)

View SolutionA particle is projected from a tower as shown in figure, then find the distance from the foot of the tower where it will strike the ground. (g=10m/s2)
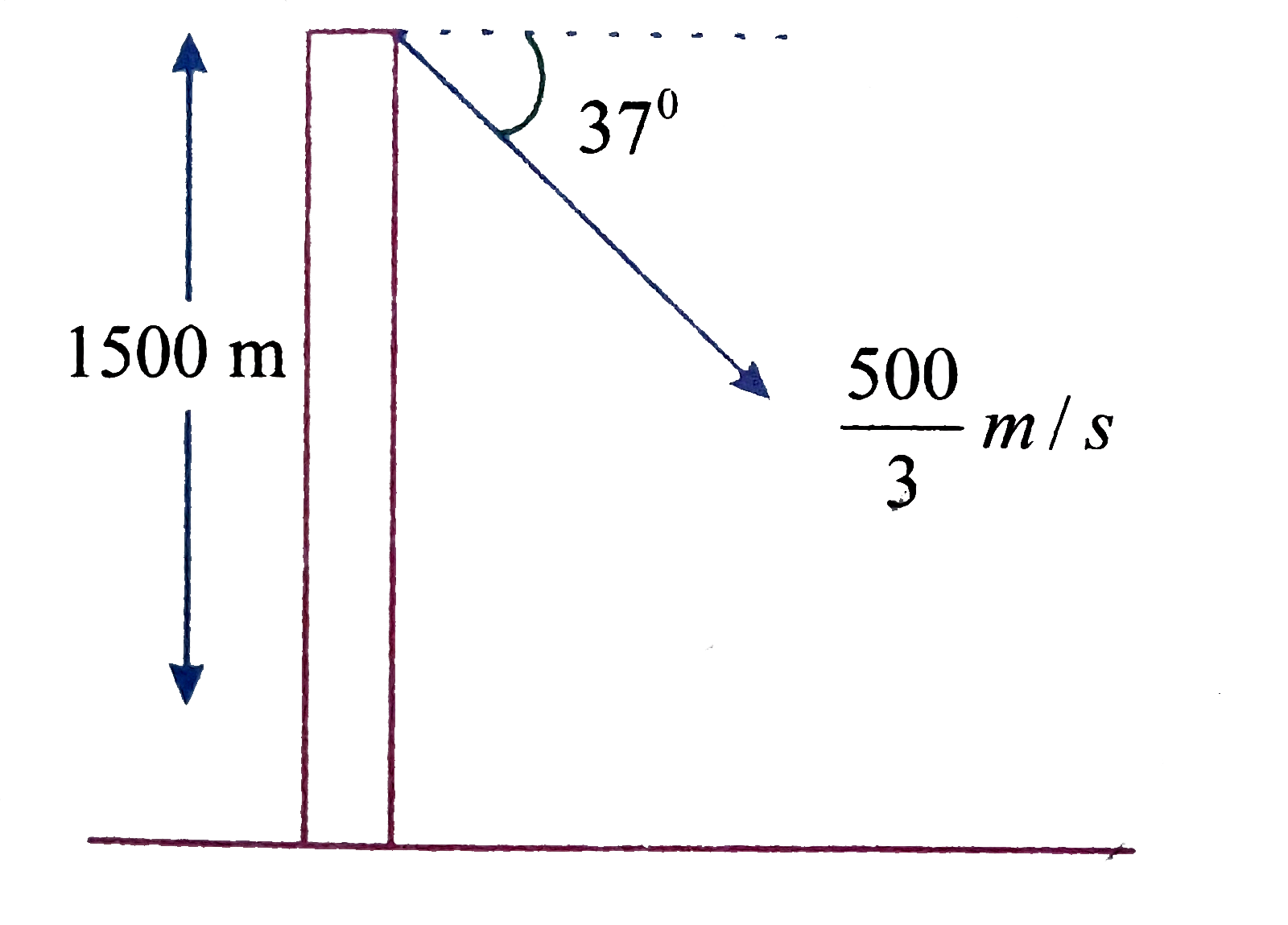
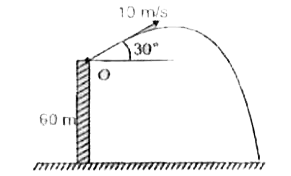
View SolutionA ball is projected from a point O as shown in figure it will strike the ground after (g = 10 m/s2 )
View Solution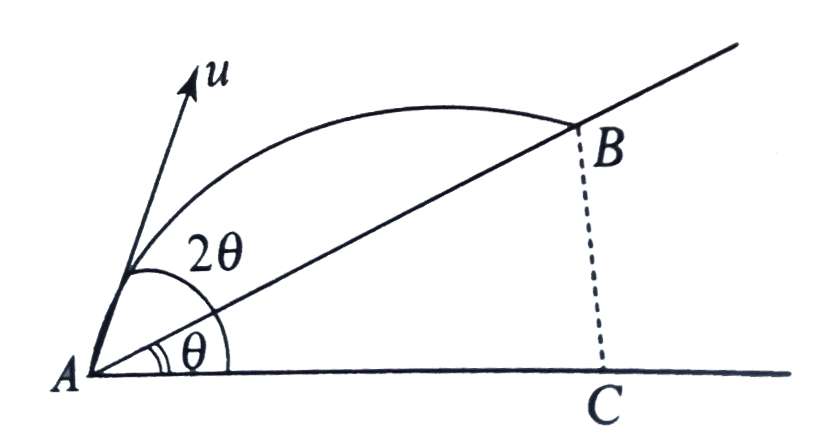
A particle is projected from point A on plane AB, so that AB=2u2tanθg√3 in the figure as shown. If u is the velocity of projection, find angle θ.
View SolutionA ball is projected from the point O with velocity 20m/s at an angle of 60∘ with horizontal as shown in figure. At highest point of its trajectory it strikes a smooth plane of inclination 30∘ at point A. The collision is perfectly inelastic. The maximum height from the ground attained by the ball is 75k meter. Find the value of k? (g=10m/s2)

View SolutionA ball strikes the ground at an angle α. and rebound at an angle β. with the verticlal as shown in the figure .Then ,

View SolutionTwo inclined planes OA and OB intersect in a horizontal plane having their inclinations αandβ with the horizontal as shown in figure. A particle is projected from P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q.
The path of the particle from P to Q is
View Solution
