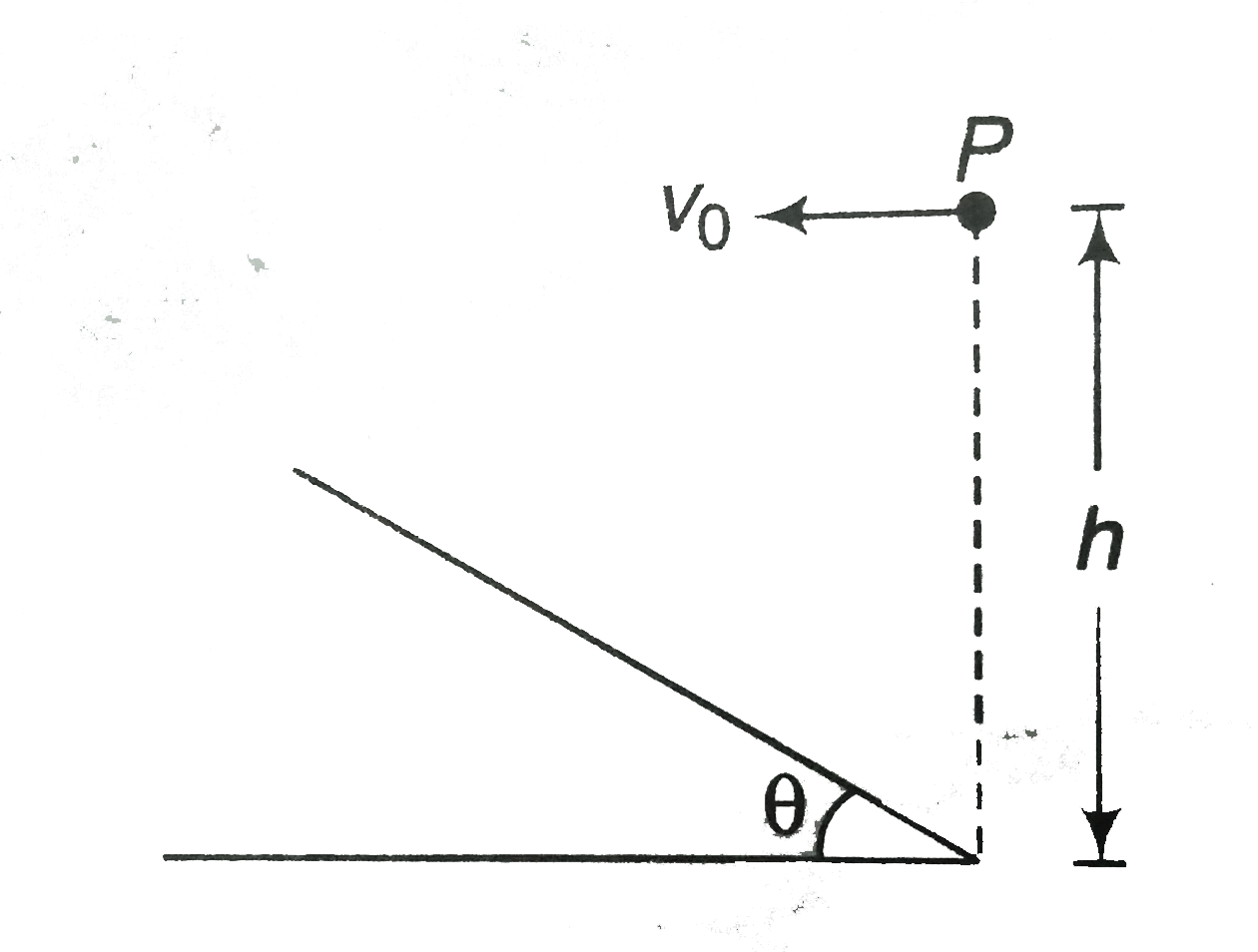
Determine the horizontal velocity with which a stone must be projected horizontally from a point P, so that it may hit the inclined plane perpendicularly. The inclination of the plane with the horizontal is and point P is at a height h above the foot of the incline, as shown in the figure.
The correct Answer is:A, B, C
,
At Q,

or ……..(i)
Solving this equation we get,
.
Topper's Solved these Questions
- PROJECTILE MOTIONBook:DC PANDEY ENGLISHChapter:PROJECTILE MOTIONExercise:Level - 2 More Than One Correct
Explore 8 Videos
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:(C )Medical entrances gallery
Explore 32 Videos
- PROPERTIES OF MATTERBook:DC PANDEY ENGLISHChapter:PROPERTIES OF MATTERExercise:Integer
Explore 8 Videos
Similar Questions
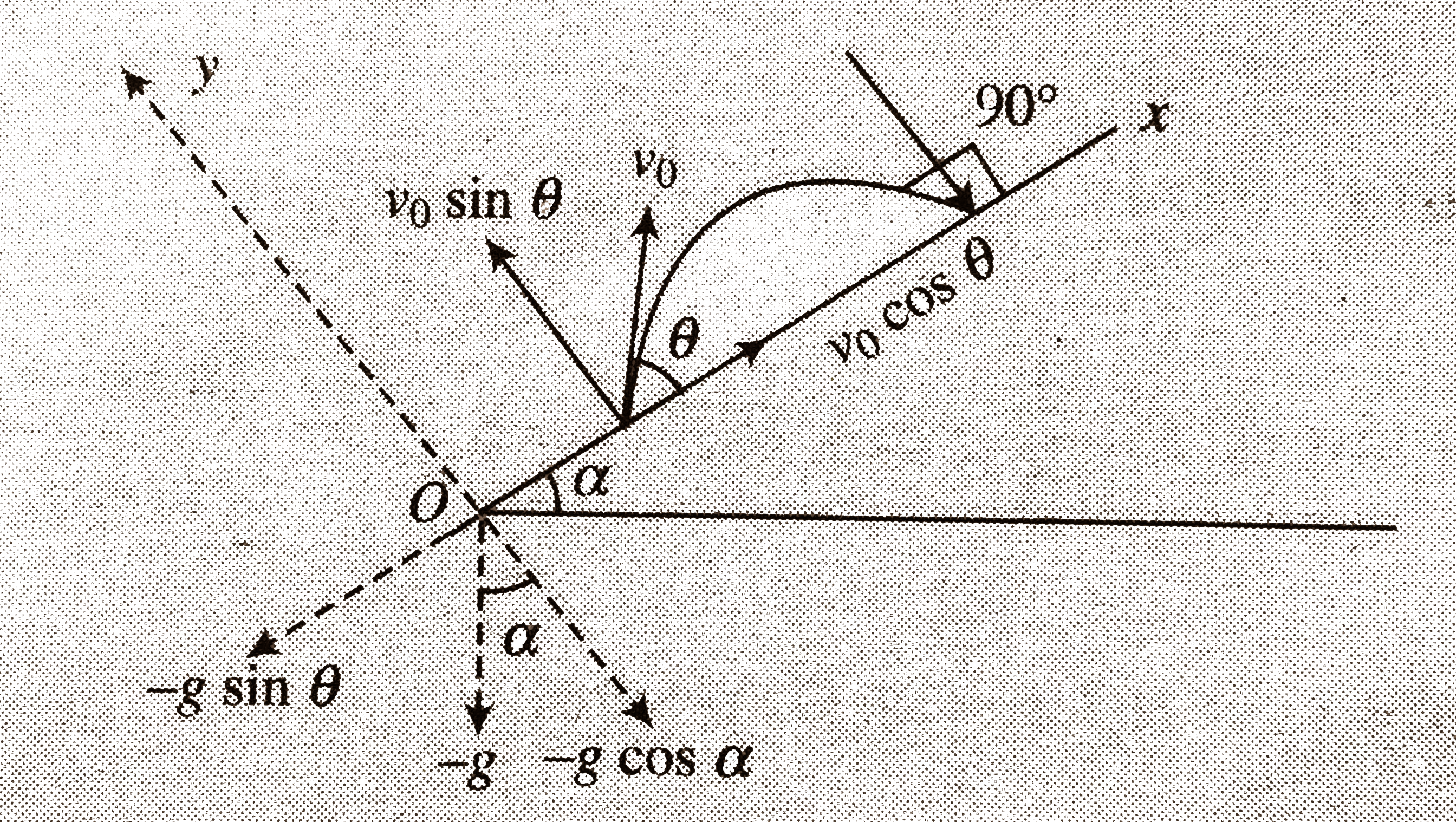
At what angle should a ball be projected up an inclined plane with a velocity v0 so that it may hit the incline normally. The angle of the inclined plane with the horizontal is ∝.
 .
.
View SolutionA stone must be projected horizontally from a point P, which is h meter above the foot of a plane inclined at an angle θ with horizontal as shown in figure . Calculate the velocity v of the stone so that in may hit the incline plane perpendiculary.

View SolutionIn figure, the angle of inclination of the inclined plane is 30∘. Find the horizontal velocity V0 so that the particle hits the inclined plane perpendicularly.
 .
.
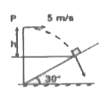
View SolutionA particle of mass m is thrown horizontally from point P , as shown in the figure, with speed 5m/s. It strikes an inclined plane perpendicularly as shown. The inclination of the plane is 30∘ with the horizontal. Then, the height h shown in the figure is ( Take g=10m/s2 ) .
View SolutionThe velocity of a sphere rolling down an inclined plane of height h at an inclination θ with the horizontal, will be :
View SolutionA projectile si thrown with velocity of 50m/s towards an inclined plane from ground such that is strikes the inclined plane perpendiclularly. The angle of projection of the projectile is 53∘ with the horizontal and the inclined plane is inclined at an angle of 45∘ to the horizonta..

(a) Find the time of flight.
(b) Find the distance between the point of projection and the foot of inclined plane.
View SolutionA ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time

View SolutionA particle is projected horizontally with spee u from point A, which is 10 above the ground . If the particle hits the inclined perpendicularly at point B. [ g =10m/s2]
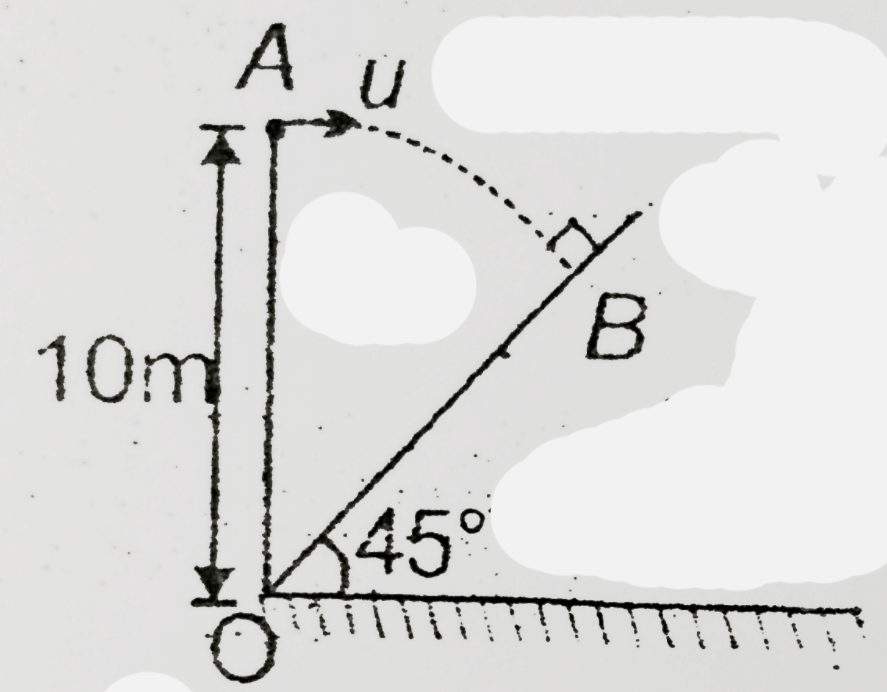
Find the length OB along the inclined plane
View SolutionA ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
View SolutionA particle is projected horizontally with speed u from point A, which is 10 above the ground . If the particle hits the inclined perpendicularly at point B. [ g =10m/s2]
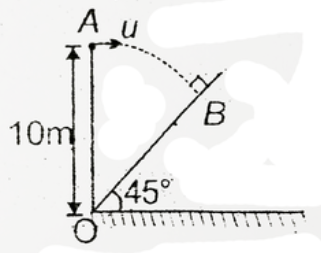
Find horizontal speed with which the particle was projected
View Solution

