At what angle should a ball be projected up an inclined plane with a velocity v0 so that it may hit the incline normally. The angle of the inclined plane with the horizontal is ∝.
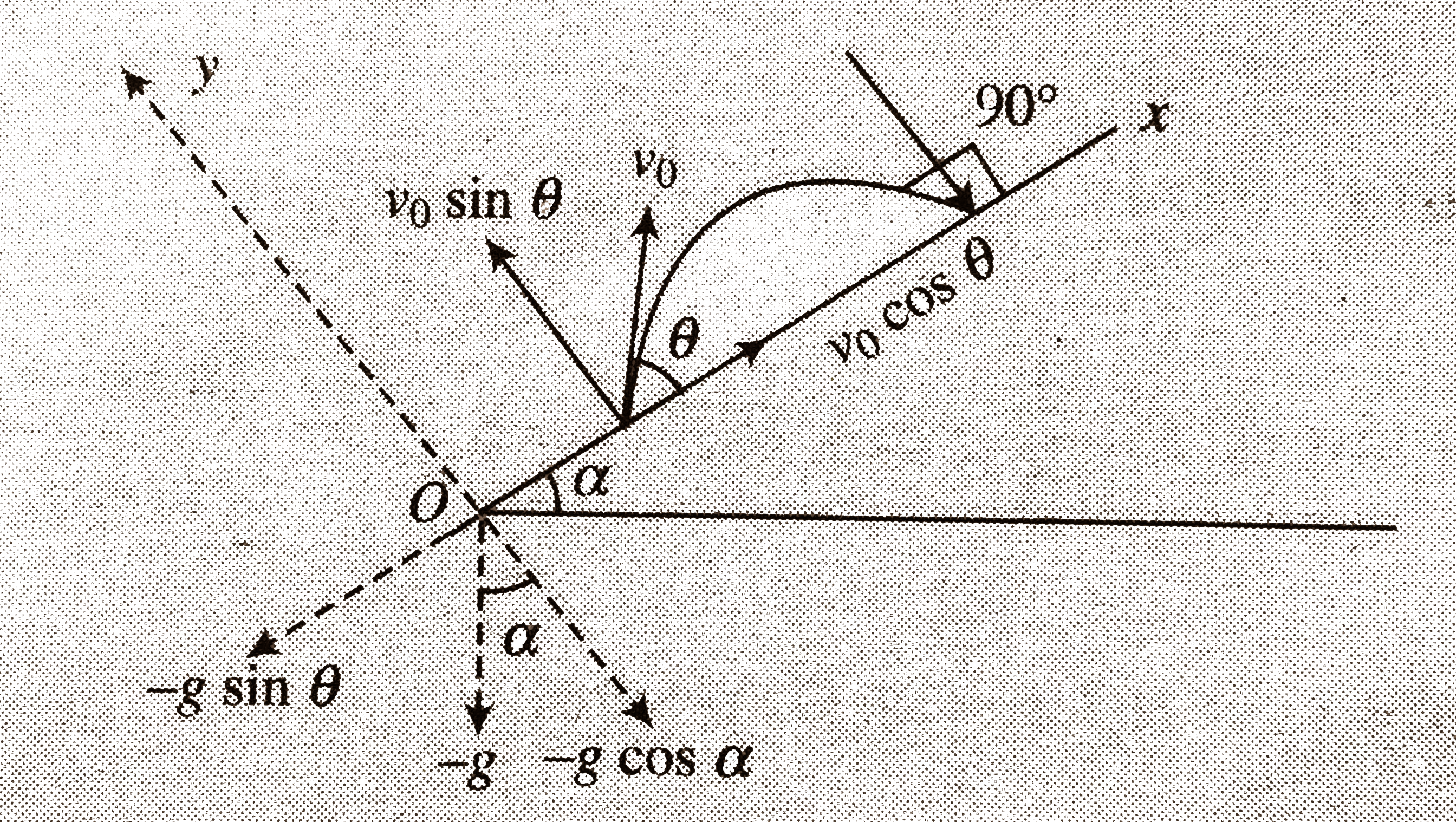 .
.
As the ball has to hit the inclined plane normally, in that position the x - component of velocity will be zero and the velocity will have y - component only.
The ball will hit the incline normally if its parallel component of velocity reduces to zero during the time of flight.
By analyzing this motion along incline, i.,e., s - direction,
vx=ux+axt
Here vx=0,ux=v0cosθ,ax=−gsin∝
0=v0cosθ−(gsin∝)T⇒T=v0cosθgsin∝...(i)
Also the displacement of the particle in y - direction will be zero. Using
y=uyt+12ayt2⇒0=v0sinθT−12gcosT2
This gives T=2v0sinθgcos∝
From (i) and (ii), we have
v0cosθgsin∝=2v0sinθgcos∝
⇒cosθsin∝=2sinθcos∝
2tanθtan∝=1
tanθ=[12cot∝]
θ=tan−1(12cot∝)
Which is the required angle of projection.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Solved Examples
7 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.1
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
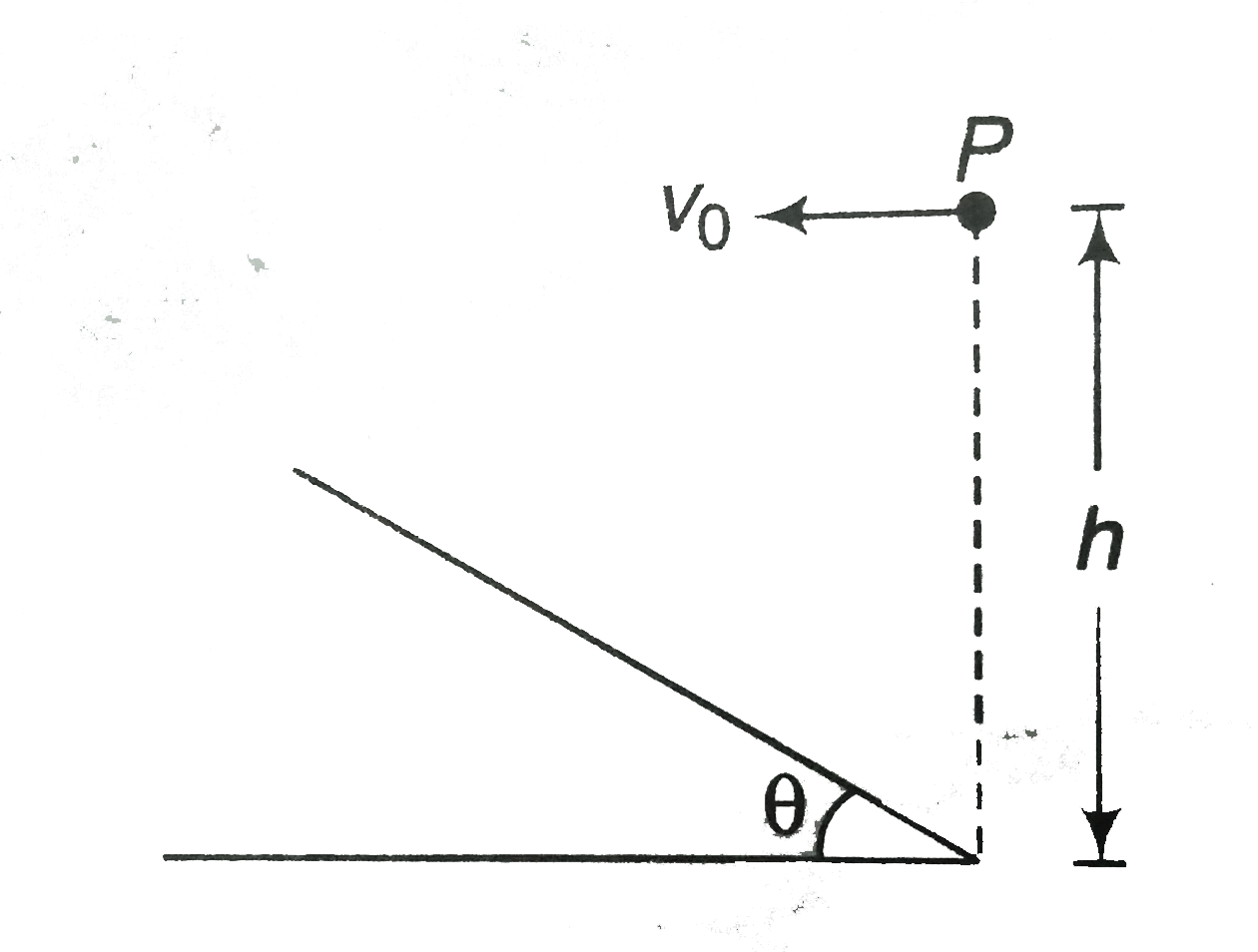
Determine the horizontal velocity v0 with which a stone must be projected horizontally from a point P, so that it may hit the inclined plane perpendicularly. The inclination of the plane with the horizontal is θ and point P is at a height h above the foot of the incline, as shown in the figure.
View SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .
.
View SolutionA ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time

View SolutionA cannon of mass 1000kg located at the base of an inclined plane fires a shell of mass 50kg in horizontal direction with velocity 180km/h. The angle of inclination of the inclined plane with the horizontal is 45∘. The coefficient of friction between the cannon and inclined plane is 0.5. The maximum height, in metre, to which the cannon can ascend the inclined plane as a result of recoil is
View SolutionA particle is projected from the inclined plane at angle 37∘ with the inclined plane in upward direction with speed 10m/s. The angle of inclined plane with horizontal is 53∘. Then the maximum height attained by the particle from the inclined plane will be-
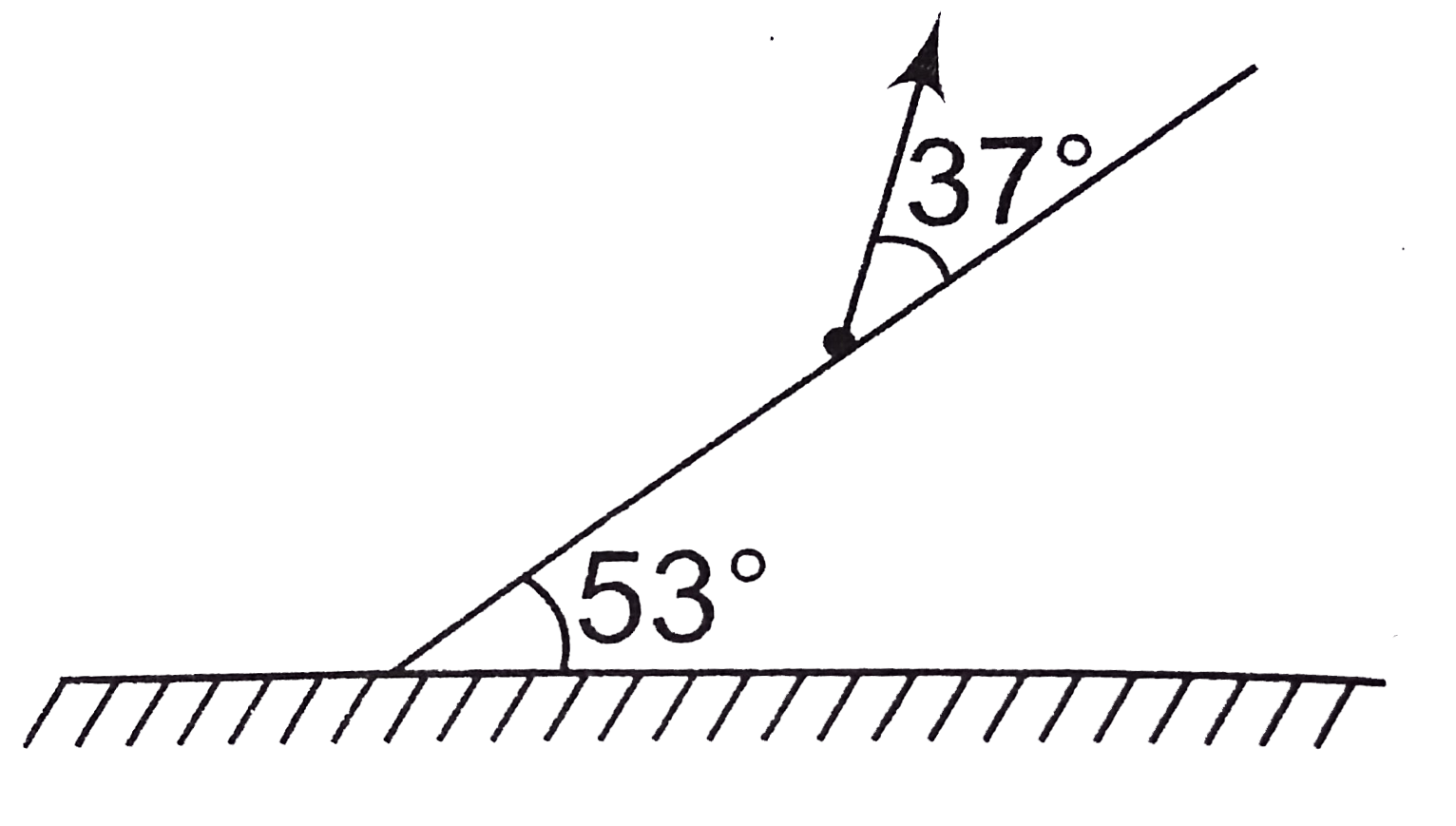
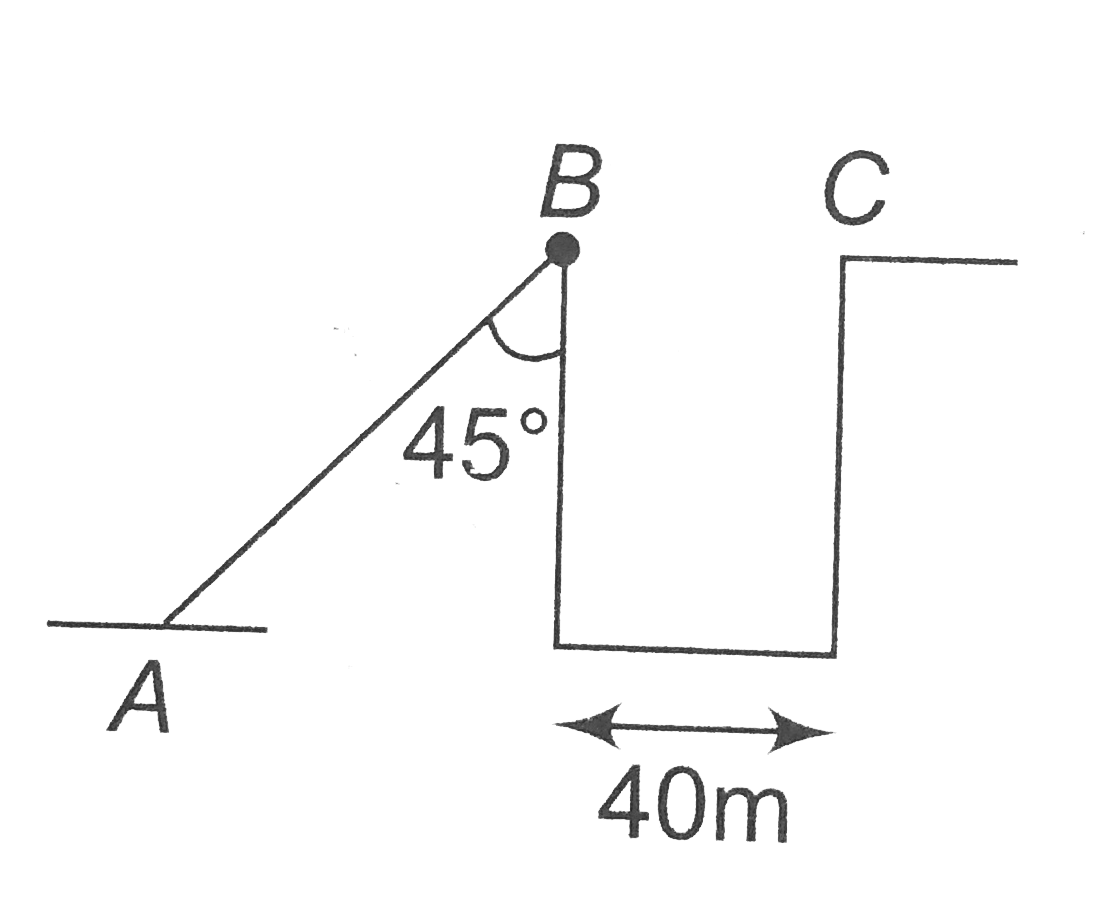
View SolutionA body is projected up a smooth inclined plane with velocity V from the point A as shown in the figure. The angle of inclination is 45∘ and the top is connected to a well of diameter 40m. If the body just manages to across the well, what is the value of V? Length of inclined plane is 20√2m.
View SolutionA ball is projected from point A with velocity 10ms−1 perpendicular to the inclined plane as shown in figure. Range of the ball on the inclined plane is

View Solution
A particle of mass m is projected up from the bottom of an inclined plane with initial velocity v0 at angle 45∘ with an inclined plane of inclination 30∘ as shown in figure. At the same time a small block of same mass m is released from rest at a height h, the particle hits the block at some point on the inclined plane. Neglect friction at inclined.
Q. The value of height h is
View SolutionA ball is projected from point A with velocity 20 m/s prependicular to the inclined plane as shown in figure. What is the range of the ball on the inclined plane ?

View SolutionA bullet is fired from the bottom of the inclined plane at angle θ=37∘ with the inclined plane. The angle of incline is 30∘ with the horizontal. Find the
(a) position of the maximum height of the bullet from the inclined plane ,
(b) time of light ,
( c) range along the incline ,
(d) the value of θ at which the range will be maximum ,
( e) maximum range.
View Solution
