A golfer standing on the ground hits a ball with a velocity of 52m/s at an angle θ above the horizontal if tanθ=512 find the time for which the ball is at least 15m above the ground?
(g=10m/s2)
The correct Answer is:(2)
To solve the problem, we need to find the time for which the ball is at least 15 meters above the ground after being hit by the golfer. We will follow these steps:
Step 1: Determine the angle θ
Given that tanθ=512, we can find sinθ and cosθ using the Pythagorean identity.
- Using the triangle formed by the opposite side (5) and adjacent side (12):
- Hypotenuse h=√52+122=√25+144=√169=13
- Therefore, sinθ=513 and cosθ=1213.
Step 2: Calculate the initial vertical velocity component (u_y)
The initial velocity u is given as 52 m/s. The vertical component of the initial velocity uy can be calculated as:
uy=usinθ=52×513=20m/s
Step 3: Write the equation for vertical motion
The height Sy of the ball at time t can be expressed using the equation of motion:
Sy=uyt−12gt2
Substituting Sy=15m, uy=20m/s, and g=10m/s2:
15=20t−12×10t2
This simplifies to:
15=20t−5t2
Rearranging gives:
5t2−20t+15=0
Dividing through by 5:
t2−4t+3=0
Step 4: Solve the quadratic equation
To find the values of t, we can factor the quadratic:
(t−1)(t−3)=0
Thus, the solutions are:
t=1sandt=3s
Step 5: Determine the time interval above 15 meters
The ball is at a height of 15 meters at t=1s and t=3s. The ball will be above 15 meters between these two times.
Thus, the time for which the ball is at least 15 meters above the ground is:
t=3s−1s=2s
Final Answer
The ball is at least 15 meters above the ground for 2 seconds.
---
Given that tanθ=512, we can find sinθ and cosθ using the Pythagorean identity.
- Hypotenuse h=√52+122=√25+144=√169=13
- Therefore, sinθ=513 and cosθ=1213.
The initial velocity u is given as 52 m/s. The vertical component of the initial velocity uy can be calculated as:
uy=usinθ=52×513=20m/s
The height Sy of the ball at time t can be expressed using the equation of motion:
Sy=uyt−12gt2
Substituting Sy=15m, uy=20m/s, and g=10m/s2:
15=20t−12×10t2
This simplifies to:
15=20t−5t2
Rearranging gives:
5t2−20t+15=0
Dividing through by 5:
t2−4t+3=0
To find the values of t, we can factor the quadratic:
(t−1)(t−3)=0
Thus, the solutions are:
t=1sandt=3s
The ball is at a height of 15 meters at t=1s and t=3s. The ball will be above 15 meters between these two times.
t=3s−1s=2s
The ball is at least 15 meters above the ground for 2 seconds.
Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Comprehension
Explore 21 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
A golfer standing on level ground hits a ball with a velocity of 52ms−1 at an angle θ above the horizontal. If tanθ=5/12, then find the time for which then ball is atleast 15m above the ground (takeg=10ms−2).
View SolutionA boy throws a ball with a velocity of 15 m/s at an angle of 15° with the horizontal. The distance at which the ball strikes the ground is
View Solution
Knowledge Check
A body is thrown with a velocity of 9.8 m/s making an angle of 30∘ with the horizontal. It will hit the ground after a time
A3 sB2sC1.5 sD1 sA ball is thrown from the top of a tower with an initial velocity of 10m/s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
A5 mB20 mC15 mD10 m
A football player throws a ball with a velocity of 50m/s at an angle 30 degrees from the horizontal. The ball remains in the air for (g=10m/s2)
View SolutionA boy playing on the roof of a 10 m high building throws a ball with a speed of 10 m/s at an angle 30∘ with the horizontal. How far from the throwing point will the ball be at the height of 10 m from the ground?
(g=10m/s2)
View SolutionA ball is thrown from the top of a tower with an intial velocity of 10 m//s at an angle 37∘ above the horizontal, hits the ground at a distance 16 m from the base of tower. Calculate height of tower. [g=10m/s2]
View SolutionA ball is thrown at a speed of 20 m/s at an angle of 30∘ with the horizontal . The maximum height reached by the ball is
(Use g=10m/s2)
View SolutionA ball is thrown from the top of 36m high tower with velocity 5m/ss at an angle 37∘ above the horizontal as shown. Its horizontal distance on the ground is closest to [g=10m/s2
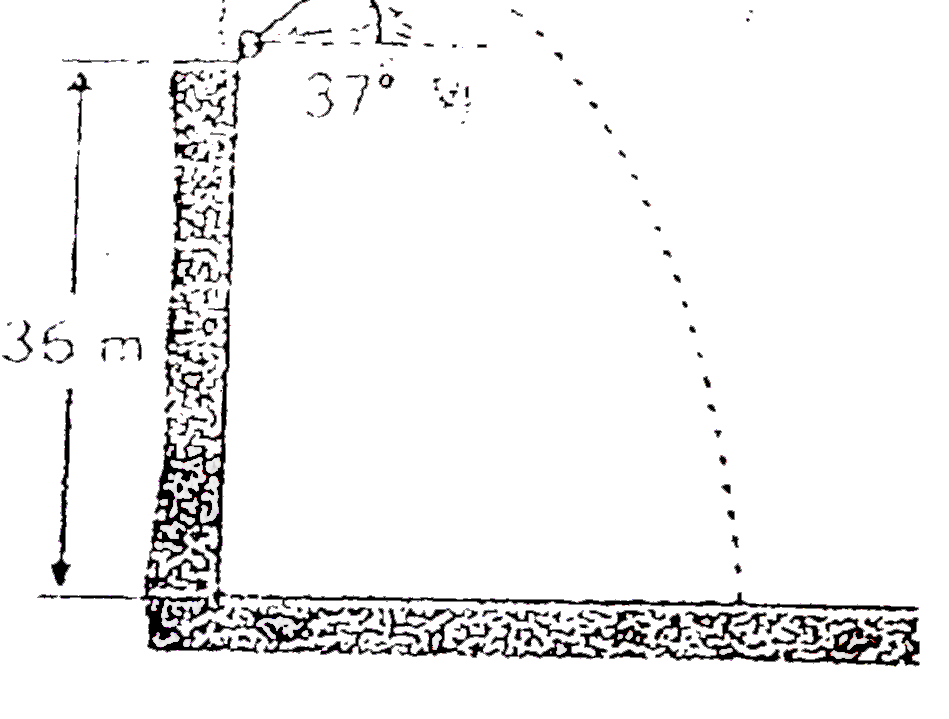 :
:
View SolutionA ball of mass 50 g is dropped from a height of 20 m. A boy on the ground hits the ball vertically upwards with a bat with an average force of 200 N, so that it attains a vertical height of 45 m. The time for which the ball remains in contact with the bat is [Take g=10m/s2]
View Solution