A cannon of mass 1000kg located at the base of an inclined plane fires a shell of mass 50kg in horizontal direction with velocity 180km/h. The angle of inclination of the inclined plane with the horizontal is 45∘. The coefficient of friction between the cannon and inclined plane is 0.5. The maximum height, in metre, to which the cannon can ascend the inclined plane as a result of recoil is
56
524
512
none of these
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Convert the shell's velocity from km/h to m/s
The shell's velocity is given as 180km/h. We need to convert this to meters per second (m/s) using the conversion factor 1km/h=13.6m/s.
vshell=180km/h×1m/s3.6km/h=50m/s
Step 2: Apply conservation of momentum
Before the cannon fires, its momentum is zero. After firing, the momentum of the shell and the cannon must be equal and opposite.
Let v be the recoil velocity of the cannon. The mass of the cannon is 1000kg and the mass of the shell is 50kg.
Using conservation of momentum:
0=(50kg×50m/s)+(1000kg×v)
Solving for v:
1000v=−2500⟹v=−25001000=−2.5m/s
Step 3: Calculate the effective velocity of the cannon along the incline
Since the cannon moves up the incline at an angle of 45∘, the effective velocity vcannon along the incline is:
vcannon=vcos(45∘)=−2.5×1√2=−2.5√2≈−1.77m/s
Step 4: Calculate the frictional force
The frictional force Ff acting on the cannon is given by:
Ff=μmgcos(45∘)
Where:
- μ=0.5
- m=1000kg
- g=10m/s2
Calculating Ff:
Ff=0.5×1000×10×1√2=5000√2≈3535.53N
Step 5: Apply the work-energy principle
The work done against friction as the cannon moves up the incline is equal to the change in kinetic energy.
The initial kinetic energy of the cannon is:
KEinitial=12mv2cannon=12×1000×(−1.77)2≈1565.45J
The work done against friction while moving up height h is:
W=Ff⋅h=5000√2⋅h
Setting the work done equal to the initial kinetic energy gives:
5000√2h=1565.45
Step 6: Solve for height h
Rearranging the equation to find h:
h=1565.45⋅√25000≈1565.45⋅1.4145000≈2212.125000≈0.4424m
Final Answer
The maximum height to which the cannon can ascend the inclined plane as a result of recoil is approximately:
0.442m
The shell's velocity is given as 180km/h. We need to convert this to meters per second (m/s) using the conversion factor 1km/h=13.6m/s.
Before the cannon fires, its momentum is zero. After firing, the momentum of the shell and the cannon must be equal and opposite.
Since the cannon moves up the incline at an angle of 45∘, the effective velocity vcannon along the incline is:
The frictional force Ff acting on the cannon is given by:
- μ=0.5
- m=1000kg
- g=10m/s2
The work done against friction as the cannon moves up the incline is equal to the change in kinetic energy.
Rearranging the equation to find h:
The maximum height to which the cannon can ascend the inclined plane as a result of recoil is approximately:
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Multiple Correct
Explore 25 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Assertion - Reasoning
Explore 2 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Subjective
Explore 23 Videos
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
A block of weight 1 N rests on a inclined plane of inclination θ with the horizontal. The coefficient of friction between the block and the inclined plane is μ. The minimum force that has to be applied parallel to the inclined plane to make the body just move up the plane is
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View Solution
Knowledge Check
A block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A10.3NB23.8NC11.9ND6.3NA block of mass 3 kg rests on a rough inclined plane making an angle of 30∘. With the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8 NB0.7×9.8×√3 NC9.8×√3 ND0.7×9.8 N
A block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionIn figure, the angle of inclination of the inclined plane is 30∘. Find the horizontal velocity V0 so that the particle hits the inclined plane perpendicularly.
 .
.
View SolutionA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA body takes ''n'' times as much time to slide down a rough inclined plane as it takes to slide down an identical but smooth inclined plane. If the angle of inclination of the inclined plane is ''θ''. What is the coefficient of friction between the body and the rough plane ?
View SolutionBlock of mass 10 kg is moving on inclined plane with constant velocity 10 m/s. The coedfficient of kinetic friction between incline plane and block is :-
View SolutionAt what angle should a ball be projected up an inclined plane with a velocity v0 so that it may hit the incline normally. The angle of the inclined plane with the horizontal is ∝.
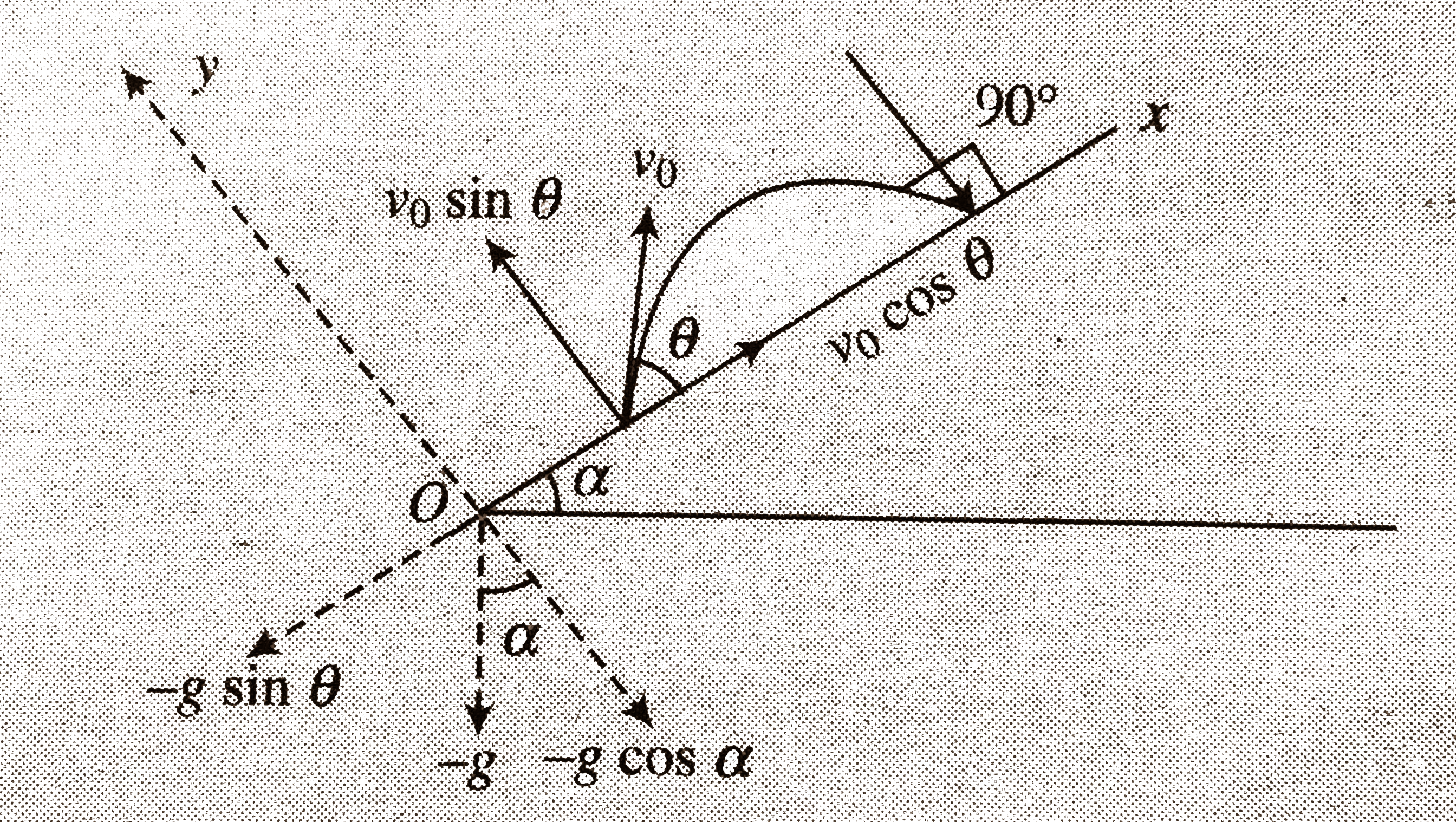 .
.
View Solution

