A particle of mass 2kg moving with a velocity of 3m/s is acted upon by a force which changes its direction of motion by an angle of 90∘ without changing its speed. What is the magnitude of impulse experienced by the particle?
6Ns
2Ns
3√2Ns
6√2Ns
The correct Answer is:D
To solve the problem step by step, we will calculate the impulse experienced by the particle as it changes its direction of motion by 90 degrees without changing its speed.
Step 1: Understand the Initial and Final Velocities
The particle has an initial mass m=2kg and is moving with an initial velocity vi=3m/s in the positive x-direction. After the force acts on it, the particle's direction changes by 90∘, and it moves in the positive y-direction with the same speed.
Step 2: Calculate the Initial Momentum
The initial momentum pi of the particle can be calculated using the formula:
pi=m⋅vi
Substituting the given values:
pi=2kg⋅3m/s=6kg m/s
Step 3: Calculate the Final Momentum
The final velocity vf is also 3m/s but in the y-direction. Therefore, the final momentum pf is:
pf=m⋅vf=2kg⋅3m/s=6kg m/s
However, since the direction has changed, we need to represent this as a vector:
pf=0^i+6^jkg m/s
Step 4: Calculate the Change in Momentum
The change in momentum Δp is given by:
Δp=pf−pi
Substituting the initial and final momentum:
Δp=(0^i+6^j)−(6^i+0^j)=−6^i+6^jkg m/s
Step 5: Calculate the Magnitude of the Change in Momentum
The magnitude of the change in momentum (which is equal to the impulse I) can be calculated using:
|I|=|Δp|=√(−6)2+(6)2
Calculating this:
|I|=√36+36=√72=6√2kg m/s
Conclusion
The magnitude of the impulse experienced by the particle is:
|I|=6√2N s
The particle has an initial mass m=2kg and is moving with an initial velocity vi=3m/s in the positive x-direction. After the force acts on it, the particle's direction changes by 90∘, and it moves in the positive y-direction with the same speed.
The initial momentum pi of the particle can be calculated using the formula:
pi=m⋅vi
Substituting the given values:
pi=2kg⋅3m/s=6kg m/s
The final velocity vf is also 3m/s but in the y-direction. Therefore, the final momentum pf is:
pf=m⋅vf=2kg⋅3m/s=6kg m/s
However, since the direction has changed, we need to represent this as a vector:
pf=0^i+6^jkg m/s
The change in momentum Δp is given by:
Δp=pf−pi
Substituting the initial and final momentum:
Δp=(0^i+6^j)−(6^i+0^j)=−6^i+6^jkg m/s
The magnitude of the change in momentum (which is equal to the impulse I) can be calculated using:
|I|=|Δp|=√(−6)2+(6)2
Calculating this:
|I|=√36+36=√72=6√2kg m/s
The magnitude of the impulse experienced by the particle is:
|I|=6√2N s
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Multiple Correct
Explore 25 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Assertion - Reasoning
Explore 2 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Subjective
Explore 23 Videos
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
A particle moving with a speed v changes direction by an angle θ, without change in speed.
View SolutionA particle of mass 120 g moving at speed of 750 cm/s is acted upon by a variable force opposite to its direction of motion. If the velocity of the particle becomes 250 cm/s along the direction of force, find the value of time 't' for which acted.
View Solution
Knowledge Check
A ball of mass m travelling horiozntally with velocity v strikes a massive vertical wall and rebounds back along its original direction with no change in speed. What is the magnitude of the impulse delivered by the wall to the ball?
A0B12mvCmvD2mv
A particle of mass 70 g, moving at 50 cm/s , is acted upon by a variable force opposite to its direction of motion. The force F is shown as a function of time t
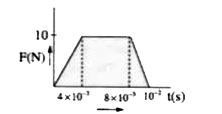
(a) its speed will be 50 cm/s after the force stops acting
(b) its direction of motion will reverse
(c) its average acceleration will be 1m/s2 during the interval in which the force acts
its average acceleration will be 10m/s2 during the interval in which the force acts
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
View SolutionA car is moving in east direction. It takes a right turn and moves along south direction without change in its speed. What is the direction of average acceleration of the car?
View SolutionA ball of mass 0⋅2 kg moving with a speed of 30 m/s strikes a bat returns in opposite direction with speed of 90m/s . Magnitude of change in momentu,m of ball will be
View SolutionA batsman deflects a ball by an angle of 60° without changing its initial speed of 20 ms−1. what is the impulse imparted to the ball if its mass is 0.15 kg?
View SolutionA body of mass 6 kg is acted on a by a force so that its velocity changes from 3ms−1 to 5ms−1, then change in momentum is
View SolutionIf a body of mass 5 kg initially at rest is acted upon by a force of 50 dyne for 3s, then the impulse will be
View Solution
