A ball of mass m is projected with a speed v into the barrel of a spring gun of mass M initially at rest lying on a frictionless surface. The mass sticks in the barrel at the point of maximum compression in the spring. The fraction of kinetic energy of the ball stored in the spring is
mM
Mm+M
mM+M
none of these
The correct Answer is:B
To solve the problem, we need to find the fraction of kinetic energy of the ball that is stored in the spring when the ball sticks in the barrel of the spring gun. Here’s a step-by-step solution:
Step 1: Understand the system
We have a ball of mass m projected with speed v into a spring gun of mass M that is initially at rest on a frictionless surface. When the ball sticks in the barrel, we need to consider the conservation of momentum.
Step 2: Apply conservation of momentum
Before the collision, the momentum of the system is just the momentum of the ball:
pinitial=mv
After the ball sticks to the spring gun, the total mass is m+M and let v′ be the speed of the combined mass after the collision. By conservation of momentum:
mv=(m+M)v′
From this, we can solve for v′:
v′=mvm+M
Step 3: Calculate initial and final kinetic energy
The initial kinetic energy Ki of the ball is:
Ki=12mv2
The final kinetic energy Kf of the system (ball + spring gun) after the collision is:
Kf=12(m+M)(v′)2
Substituting v′ from step 2:
Kf=12(m+M)(mvm+M)2
Simplifying this:
Kf=12(m+M)⋅m2v2(m+M)2=12⋅m2v2m+M
Step 4: Calculate the energy stored in the spring
The energy stored in the spring is equal to the loss of kinetic energy:
Energy stored in spring=Ki−Kf
Substituting the values:
Energy stored in spring=12mv2−12⋅m2v2m+M
Factoring out 12v2:
Energy stored in spring=12v2(m−m2m+M)
Finding a common denominator:
=12v2(m(m+M)−m2m+M)=12v2(mMm+M)
Step 5: Calculate the fraction of kinetic energy stored in the spring
The fraction of kinetic energy stored in the spring is given by:
Fraction=Energy stored in springKi=12v2(mMm+M)12mv2
Simplifying this:
=mMm+M⋅1m=Mm+M
Final Answer
The fraction of kinetic energy of the ball stored in the spring is:
Mm+M
We have a ball of mass m projected with speed v into a spring gun of mass M that is initially at rest on a frictionless surface. When the ball sticks in the barrel, we need to consider the conservation of momentum.
Before the collision, the momentum of the system is just the momentum of the ball:
pinitial=mv
After the ball sticks to the spring gun, the total mass is m+M and let v′ be the speed of the combined mass after the collision. By conservation of momentum:
mv=(m+M)v′
From this, we can solve for v′:
v′=mvm+M
The initial kinetic energy Ki of the ball is:
Ki=12mv2
The final kinetic energy Kf of the system (ball + spring gun) after the collision is:
Kf=12(m+M)(v′)2
Substituting v′ from step 2:
Kf=12(m+M)(mvm+M)2
Simplifying this:
Kf=12(m+M)⋅m2v2(m+M)2=12⋅m2v2m+M
The energy stored in the spring is equal to the loss of kinetic energy:
Energy stored in spring=Ki−Kf
Substituting the values:
Energy stored in spring=12mv2−12⋅m2v2m+M
Factoring out 12v2:
Energy stored in spring=12v2(m−m2m+M)
Finding a common denominator:
=12v2(m(m+M)−m2m+M)=12v2(mMm+M)
The fraction of kinetic energy stored in the spring is given by:
Fraction=Energy stored in springKi=12v2(mMm+M)12mv2
Simplifying this:
=mMm+M⋅1m=Mm+M
The fraction of kinetic energy of the ball stored in the spring is:
Mm+M
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A ball of mass m=6kg is shot with speed v=20m/s into a barrel of spring gun of mass M=24kg initially at rest. All surfaces are smooth & spring is massless. Speed of gun after ball stops relative to gun is
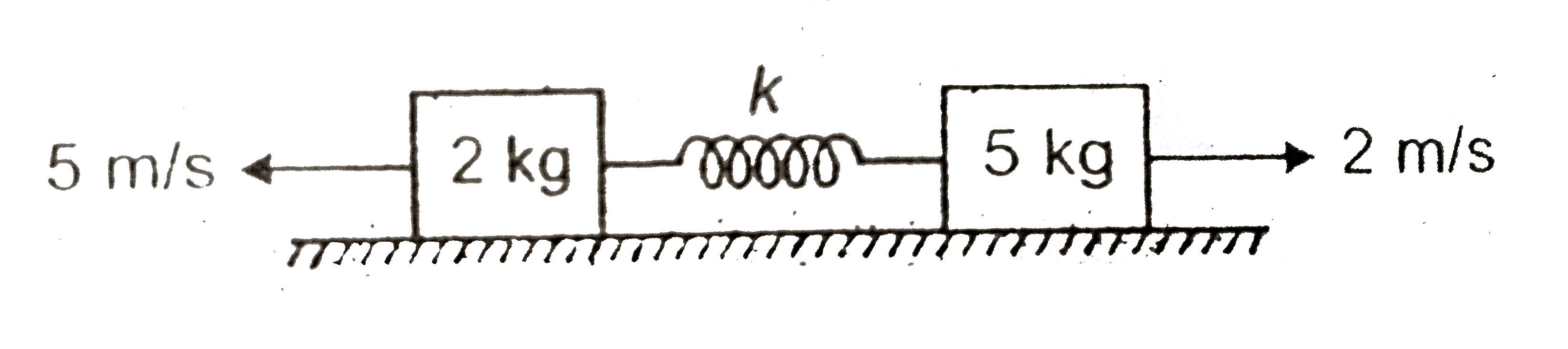
View SolutionTwo blocks of mass 2kg and 5kg are given speed as shown in the figure. System is lying on a frictionless surface and the blocks are connected by a massless spring if spring constant 35Nm. Find the maximum compression in the spring.
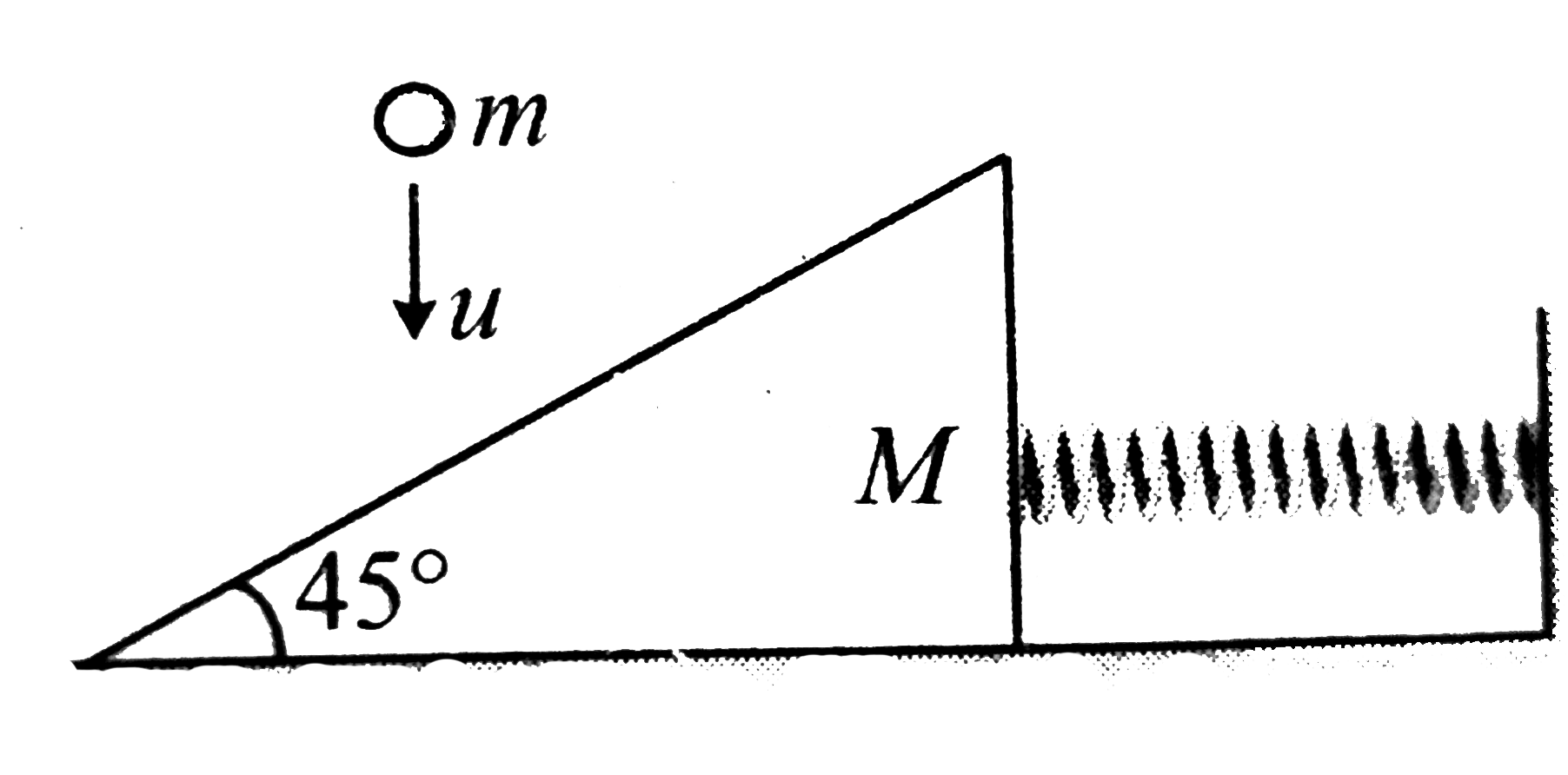
View SolutionA ball of mass m hits a wedge of mass M vertically with speed u, which is placed, on a smooth horizontal surface. Find the maximum compression in the spring, if the collision is perfectly elastic and no friction any where. Spring constant of spring is K.
View SolutionA block of mass m is relesed from rest from a height h onto a smooth surface of mass M fitted with an ideal spring of stiffness k. find the maximum compression in the spring.

View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionA ball of mass 'm' moving with speed 'u' undergoes a head-on elastic collision with a ball of mass 'nm' initially at rest. Find the fraction of the incident energy transferred to the second ball.
View SolutionThe kinetic energy of a mass connected to a spring will be maximum in :
View SolutionIn a vertical spring mass system, a block of mass m is initially at rest when there is no extension. Now if the mass is released suddenly, then the maximum elongation in the spring is
View SolutionA rod mass (M) hinged at (O) is kept in equilibrium with a spring of stiffness (k) as shown in figure. The potential energy stored in the spring is .

View SolutionA force of 10 N holds an ideal spring with a 20Nm spring constant in compression. The potential energy stored in the spring is
View Solution
