Block of mass 10 kg is moving on inclined plane with constant velocity 10 m/s. The coedfficient of kinetic friction between incline plane and block is :-
0.57
0.75
0.5
None of these
The correct Answer is:B
To solve the problem of finding the coefficient of kinetic friction (μk) between the inclined plane and the block, we can follow these steps:
Step 1: Understand the Forces Acting on the Block
The block of mass m=10kg is moving with a constant velocity of 10m/s on an inclined plane. Since it is moving with constant velocity, the net force acting on the block along the incline must be zero.
Step 2: Identify the Forces
1. Weight of the block (W): The weight acts vertically downward and is given by W=mg, where g≈9.8m/s2.
2. Normal force (N): This acts perpendicular to the inclined surface.
3. Frictional force (Ff): This opposes the motion of the block and is given by Ff=μkN.
4. Components of Weight:
- Parallel to the incline: W∥=mgsinθ
- Perpendicular to the incline: W_{\perpendicular} = mg \cos \theta
Step 3: Set Up the Equations
Since the block is moving with constant velocity, the net force along the incline is zero:
mgsinθ−Ff=0
Substituting the frictional force:
mgsinθ−μkN=0
Step 4: Calculate the Normal Force
The normal force N is equal to the perpendicular component of the weight:
N=mgcosθ
Step 5: Substitute Normal Force into the Equation
Substituting N into the friction equation:
mgsinθ−μk(mgcosθ)=0
This simplifies to:
mgsinθ=μk(mgcosθ)
Step 6: Cancel Out Common Terms
Since mg is common on both sides, we can cancel it out (assuming m≠0):
sinθ=μkcosθ
Step 7: Solve for Coefficient of Kinetic Friction
Rearranging gives:
μk=sinθcosθ=tanθ
Step 8: Calculate tanθ
Given that θ=37∘:
tan37∘=34=0.75
Final Answer
Thus, the coefficient of kinetic friction (μk) between the inclined plane and the block is:
μk=0.75
The block of mass m=10kg is moving with a constant velocity of 10m/s on an inclined plane. Since it is moving with constant velocity, the net force acting on the block along the incline must be zero.
1. Weight of the block (W): The weight acts vertically downward and is given by W=mg, where g≈9.8m/s2.
2. Normal force (N): This acts perpendicular to the inclined surface.
3. Frictional force (Ff): This opposes the motion of the block and is given by Ff=μkN.
4. Components of Weight:
- Parallel to the incline: W∥=mgsinθ
- Perpendicular to the incline: W_{\perpendicular} = mg \cos \theta
Since the block is moving with constant velocity, the net force along the incline is zero:
mgsinθ−Ff=0
Substituting the frictional force:
mgsinθ−μkN=0
The normal force N is equal to the perpendicular component of the weight:
N=mgcosθ
Substituting N into the friction equation:
mgsinθ−μk(mgcosθ)=0
This simplifies to:
mgsinθ=μk(mgcosθ)
Since mg is common on both sides, we can cancel it out (assuming m≠0):
sinθ=μkcosθ
Rearranging gives:
μk=sinθcosθ=tanθ
Given that θ=37∘:
tan37∘=34=0.75
Thus, the coefficient of kinetic friction (μk) between the inclined plane and the block is:
μk=0.75
Topper's Solved these Questions
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (WORK POWER & ENERGY)
Explore 34 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (CIRCULAR MOTION)
Explore 17 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (NEWTONS LAWS OF MOTION)
Explore 46 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
Similar Questions
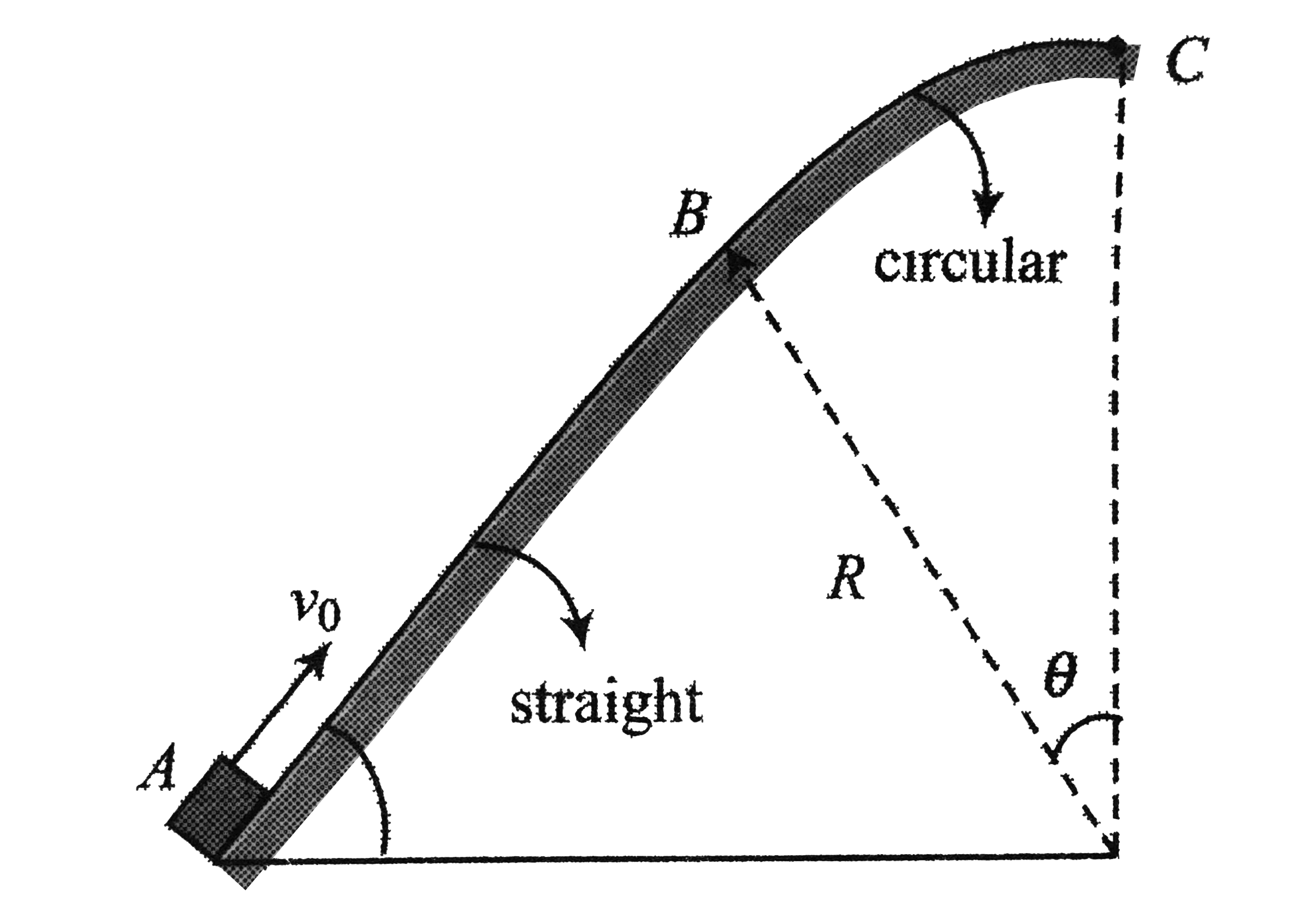
A block of mass m is projected up with a velocity v0 along an inclined plane of angle of inclination θ=37∘. The coefficient of friction between the inclined plane AB and blocks is μ(=tanθ). Find the values of v0 so that the block moves in a circular path from B to C.
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View Solution
Knowledge Check
A block of mass 3 kg rests on a rough inclined plane making an angle of 30∘. With the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8 NB0.7×9.8×√3 NC9.8×√3 ND0.7×9.8 NA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A10.3NB23.8NC11.9ND6.3N
A block of mass m=2kg is resting on a inclined plane of inclination 30∘ The coefficient of friction between the block and the plane is μ=0.5 what minimum force F (in newton) should be applied perpendicular to the plane on the block so that the does not slip on the plane?

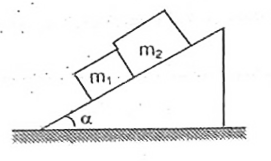
View SolutionTwo blocks of masses m1andm2 are kept touching each other on a rough fixed inclined plane of inclination α. Coefficients of kinetic friction between the inclined plane and the block m1 is k1 and between the inclined plane and block m2 is k2. Find the force of interaction between the blocks in the process of motion.
View SolutionA block of mass m is placed over rough inclined plane having inclination 30∘ .The co-efficient of friction between the block and inclined plane is 0.75.The contact force on the block is x4mg. Find the value of x
View SolutionA particle of mass 5kg is moving on rough fixed inclined plane with constant velocity of 5m/s as shown in the figure. Find the friction force acting on a body by plane.

View SolutionA block of mass 2 kg slides down an incline plane of inclination 30°. The coefficient of friction between block and plane is 0.5. The contact force between block and plank is :
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View Solution

