A ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time

The correct Answer is:D
Step by step video & image solution for A ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
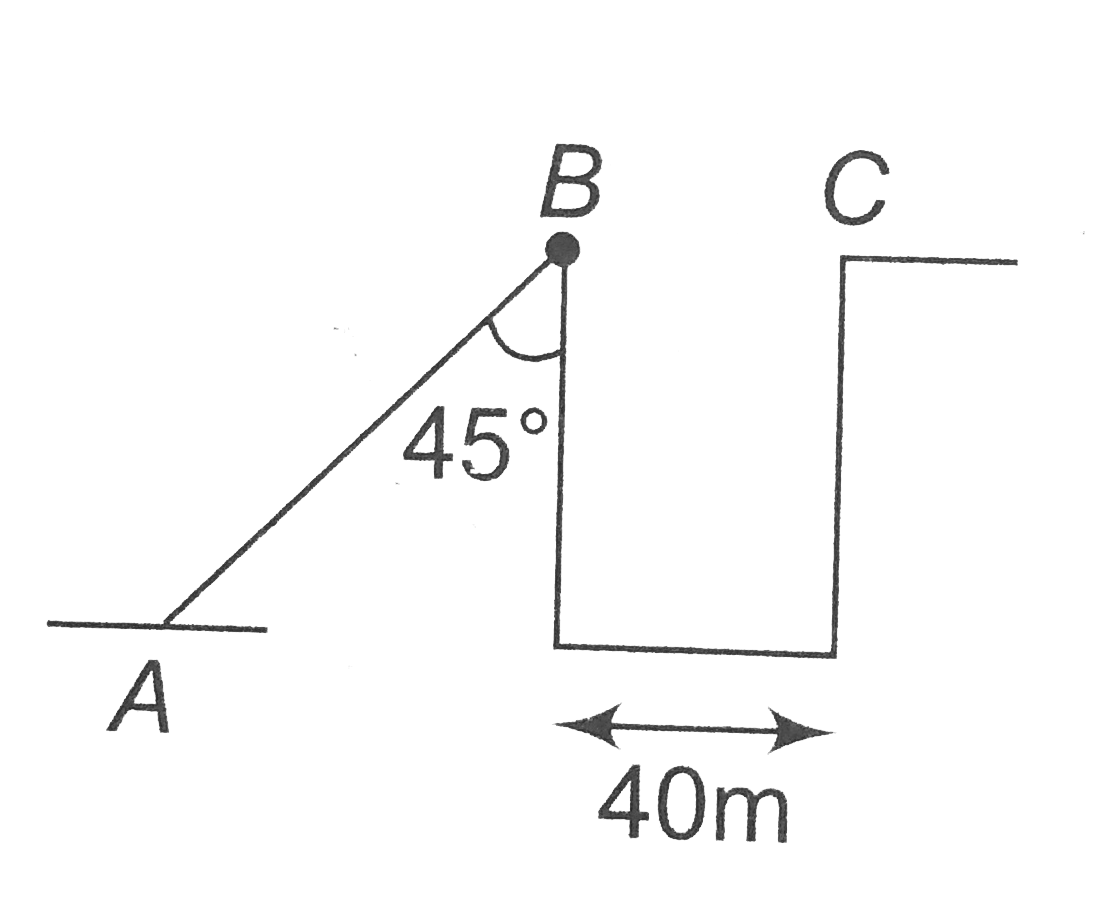
A body is projected up a smooth inclined plane with velocity V from the point A as shown in the figure. The angle of inclination is 45∘ and the top is connected to a well of diameter 40m. If the body just manages to across the well, what is the value of V? Length of inclined plane is 20√2m.
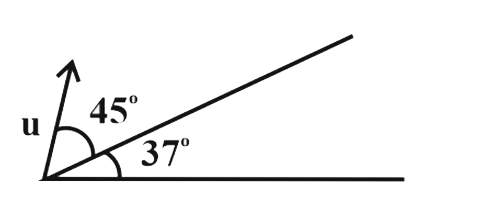
View SolutionA particle is projected on a frictionless inclined plane of inclination 37∘ at an angle of projection 45∘ from the inclined plane as shown in the figure. If after the first collision from the plane, the particle returns to its point of projection, then what is the value of the reciprocal of the coefficient of restitution between the particle and the plane?
View SolutionA ball is projected from a point O as shown in figure it will strike the ground after (g = 10 m/s2 )

View SolutionA ball is projected perpendicularly from an inclined plane of angle θ, with speed 'u' as shown. The time after which the projectile is making angle 45∘ with the inclined plane is :

View SolutionA particle is projected from a point A with velocity √2u an angle of 45∘ with horizontal as shown in figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is

View SolutionA stone is projected from point P on the inclined plane with velocity v0=10m/sec directed perpendicular to the plane. The time taken (in second) by the stone to strike the horizontal ground S is (Given PO=l=10meter)(Take g=10m/s2)

View SolutionA ball is thrown horizontally from a point O with speed 20 m/s as shown. Ball strikes the incline plane along the normal to it after two seconds. Find value of x, if β=π/x (where β is the angle of incline in degree)

View SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .
.
View SolutionA ball is projected from point A with velocity 20 m/s prependicular to the inclined plane as shown in figure. What is the range of the ball on the inclined plane ?

View SolutionA particle is projected with a certain velocity at an angle ∝ above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally, then ∝ is equal to.
View Solution

