A ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
2v2g
√2[2v2g]
v2g
√2v2g
The correct Answer is:b
To solve the problem of how far from the point of projection the ball strikes the inclined plane, we can follow these steps:
Step 1: Understand the motion
The ball is projected horizontally from the top of an inclined plane at an angle of 45∘ with the horizontal. The initial velocity of the ball is v and it moves under the influence of gravity.
Step 2: Set up the coordinate system
Let’s define our coordinate system:
- The x-axis is along the inclined plane.
- The y-axis is perpendicular to the inclined plane.
Step 3: Determine the equations of motion
Since the ball is projected horizontally, its initial vertical velocity is 0. The motion can be analyzed separately in the horizontal (x) and vertical (y) directions.
1. Horizontal motion:
- The horizontal distance traveled by the ball is given by:
x=vt
2. Vertical motion:
- The vertical distance traveled by the ball under gravity is given by:
y=12gt2
Step 4: Relate the vertical and horizontal distances
Since the inclined plane makes an angle of 45∘ with the horizontal, the relationship between x and y can be expressed as:
y=xtan(45∘)=x
This means that the vertical distance y is equal to the horizontal distance x when the angle is 45∘.
Step 5: Substitute y in terms of x
From the vertical motion equation, we have:
y=12gt2
Setting y=x, we get:
x=12gt2
Step 6: Substitute t from horizontal motion
From the horizontal motion equation x=vt, we can express time t as:
t=xv
Substituting this into the equation for y:
x=12g(xv)2
Step 7: Solve for x
Rearranging the equation gives:
x=12gx2v2
Multiplying both sides by 2v2 and rearranging, we get:
2vx=gx2
gx2−2vx=0
Factoring out x:
x(gx−2v)=0
This gives us two solutions: x=0 (the point of projection) or gx=2v. Solving for x:
x=2vg
Step 8: Calculate the distance along the incline
The distance l along the incline can be calculated using the Pythagorean theorem:
l=√x2+y2
Since y=x:
l=√x2+x2=√2x2=x√2
Substituting x=2v2g:
l=√2⋅2v2g=2√2v2g
Final Answer
The distance from the point of projection to where the ball strikes the inclined plane is:
l=2√2v2g
The ball is projected horizontally from the top of an inclined plane at an angle of 45∘ with the horizontal. The initial velocity of the ball is v and it moves under the influence of gravity.
Let’s define our coordinate system:
- The x-axis is along the inclined plane.
- The y-axis is perpendicular to the inclined plane.
Since the ball is projected horizontally, its initial vertical velocity is 0. The motion can be analyzed separately in the horizontal (x) and vertical (y) directions.
- The horizontal distance traveled by the ball is given by:
x=vt
- The vertical distance traveled by the ball under gravity is given by:
y=12gt2
Since the inclined plane makes an angle of 45∘ with the horizontal, the relationship between x and y can be expressed as:
y=xtan(45∘)=x
This means that the vertical distance y is equal to the horizontal distance x when the angle is 45∘.
From the vertical motion equation, we have:
y=12gt2
Setting y=x, we get:
x=12gt2
From the horizontal motion equation x=vt, we can express time t as:
t=xv
Substituting this into the equation for y:
x=12g(xv)2
Rearranging the equation gives:
x=12gx2v2
Multiplying both sides by 2v2 and rearranging, we get:
2vx=gx2
gx2−2vx=0
Factoring out x:
x(gx−2v)=0
This gives us two solutions: x=0 (the point of projection) or gx=2v. Solving for x:
x=2vg
The distance l along the incline can be calculated using the Pythagorean theorem:
l=√x2+y2
Since y=x:
l=√x2+x2=√2x2=x√2
Substituting x=2v2g:
l=√2⋅2v2g=2√2v2g
The distance from the point of projection to where the ball strikes the inclined plane is:
l=2√2v2g
Topper's Solved these Questions
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Relative Velocity In Two Dimensions
Explore 23 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Kinematics Of Circular Motion
Explore 26 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Projectile From A Height And Movingframe
Explore 19 Videos
- MOCK TESTBook:A2ZChapter:MOCK TESTExercise:Motion With Constant Acceleration
Explore 15 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Chapter Test
Explore 30 Videos
Similar Questions
A particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle is projected horizontal with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane?
View Solution
Knowledge Check
A particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle θ=37∘ to the horizontal (g=10m/s2)
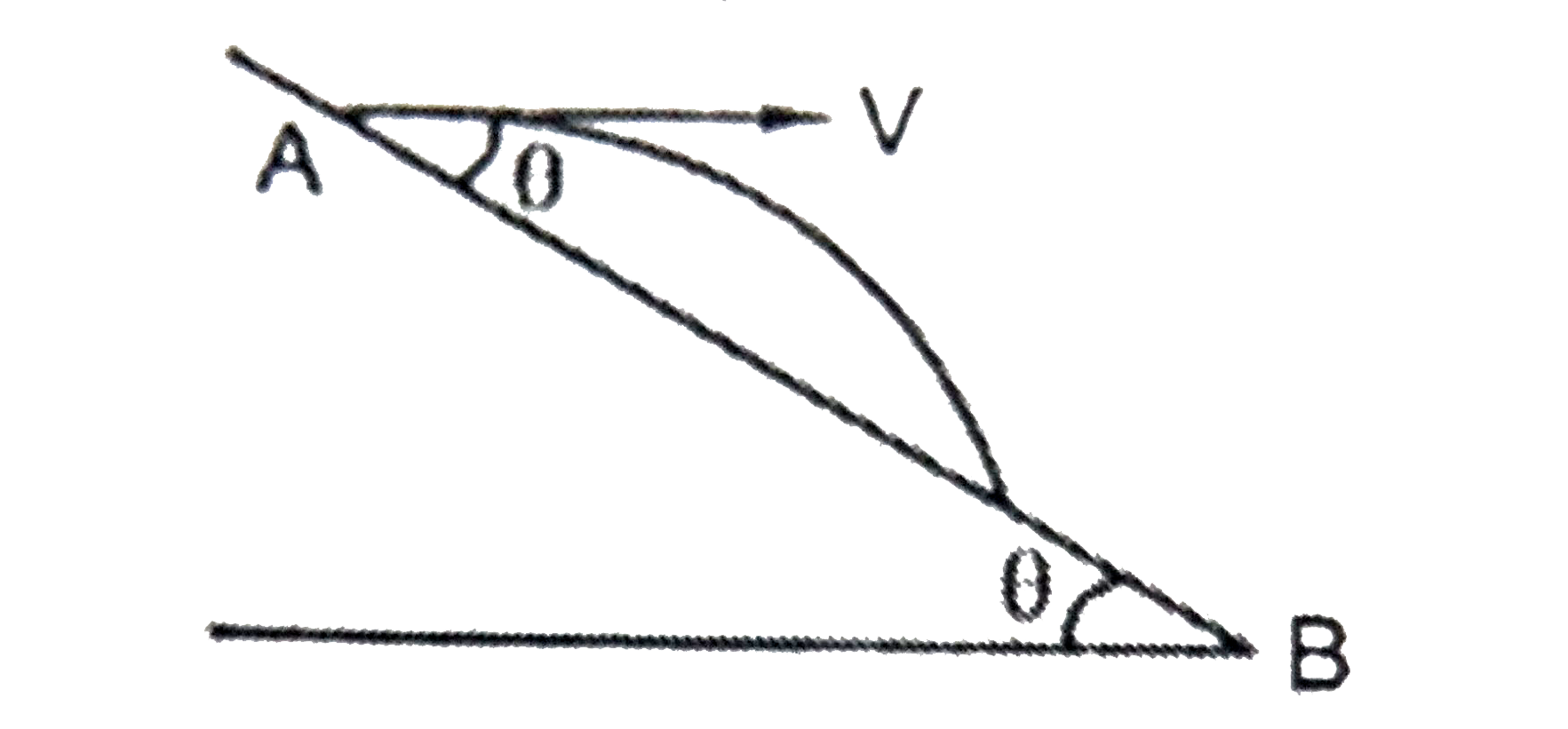
How far from the point of projection will the particle strike the plane?A75mB6516mC7516mD859mA particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle θ=37∘ to the horizontal (g=10m/s2)
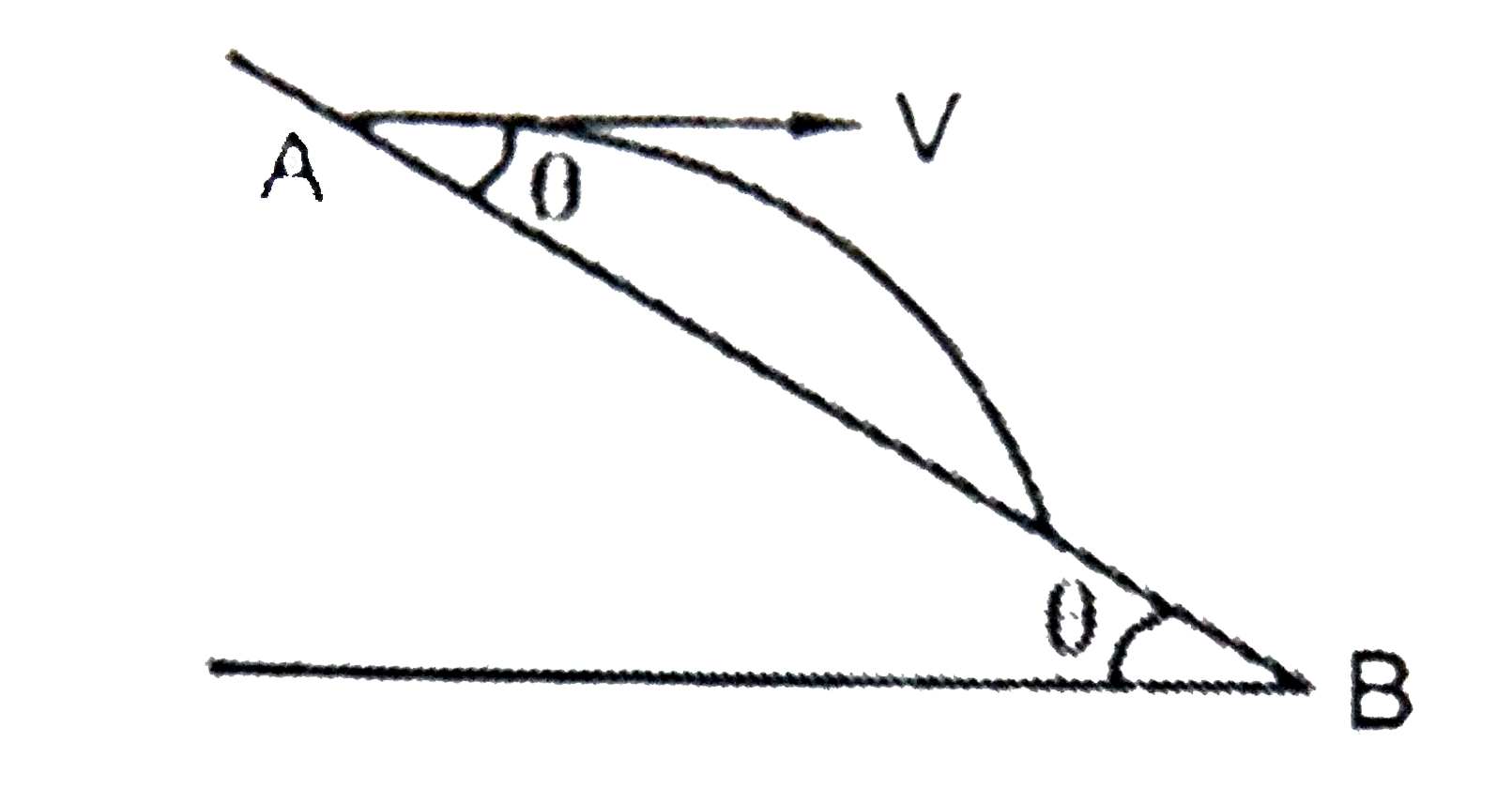
Find the time taken by the particle to hit the plane.A34sB3sC4sD43sA particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle θ=37∘ to the horizontal (g=10m/s2)
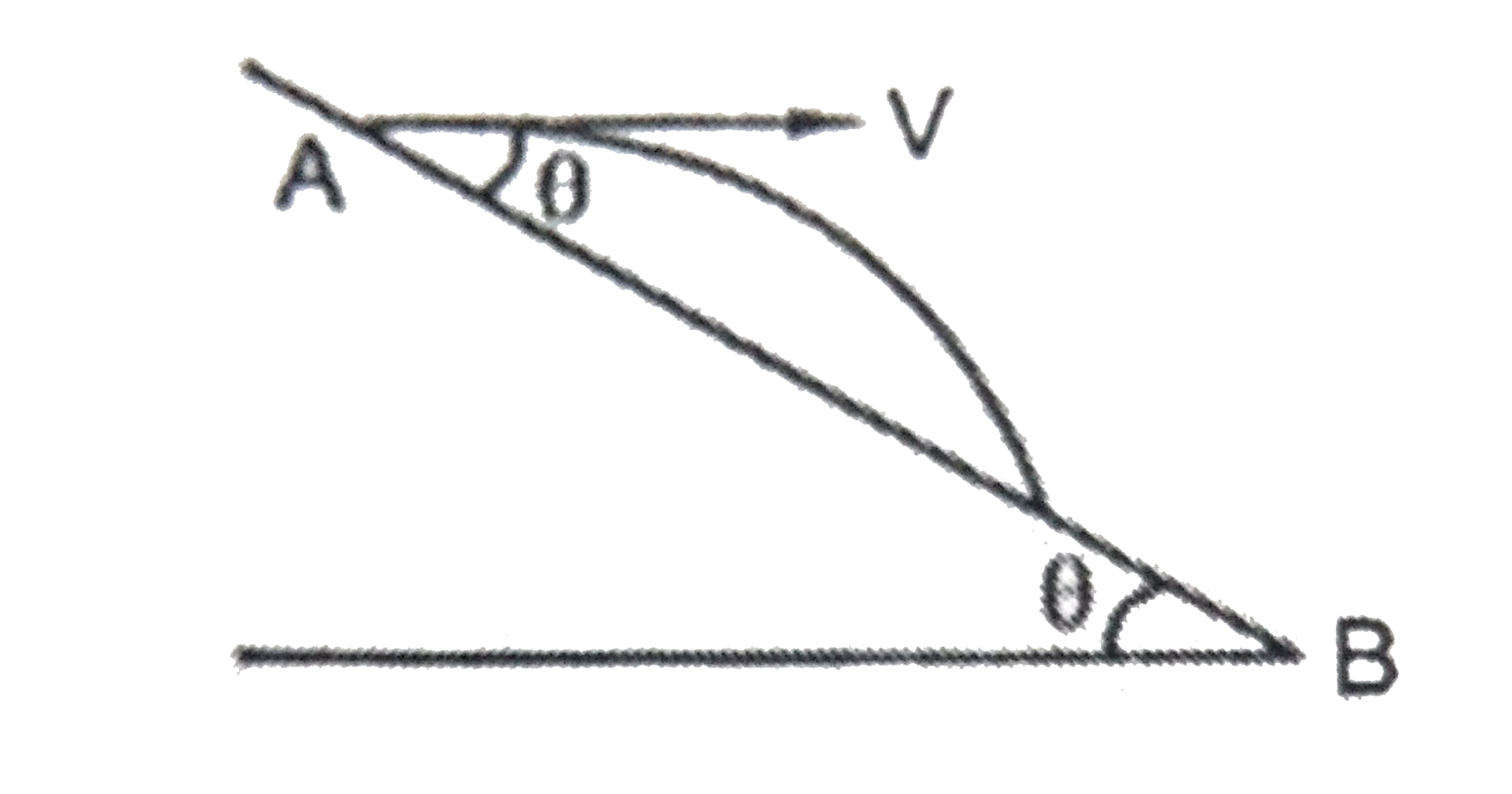
What is the velocity of the particle just before it hits the plane?A5√3m/sB52√13m/sC10√13m/sD5√26m/s
A pariicle is projected horizontally with a speed (u) from top of a plance inclined at anangle θ with the horizontal direction. How far from the point of projection will the particle strike the plane ?
View SolutionA particles is projected horizontally with a speed v from the top of a plane inclined at an angle tehta to the horizontal as shown in the figure.
(a) Hwo far from the point of projection will the particle strike the plane ?
(b) Find the time taken by the particel to hit the plane.
(c) What is the velocity of particle just before it hits the plane ?
View SolutionA ball is projected horizontally with a speed u from the top of inclined plane of inclination α with horizontal. At what distance along the plane, the ball will strike the plane ?
View SolutionA particle is thrown horizontally from the top of an inclined plane , with a speed of 5m/s . If the inclination of the plane is 30∘ with the horizontal , how far from the point of projection will the particle strike the plane ?
View SolutionA ball is projected horizontal from the top of a tower with a velocity v0. It will be moving at an angle of 60∘ with the horizontal after time.
View Solution

