If the particle is projected down onto the inclined plane at same speed and angle with the inclined plane the ratio of the time of flight and time of flight for upward projection is :
1:√2
√2:1
1:1
none of these
The correct Answer is:C
Time of flight will be same in both cases, because uy is same in both cases.
Topper's Solved these Questions
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Relative Velocity In Two Dimensions
Explore 23 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Kinematics Of Circular Motion
Explore 26 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Projectile From A Height And Movingframe
Explore 19 Videos
- MOCK TESTBook:A2ZChapter:MOCK TESTExercise:Motion With Constant Acceleration
Explore 15 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Chapter Test
Explore 30 Videos
Similar Questions
An particle is projected with velocity u on an inclined plane at an angle θ with the plane. If the particle lands on the plane at right Angle and its time of flight is ucosecθ2g. Find the angle of inclination of the plane with horizontal.
View SolutionDownward Projection On An Inclined Plane
View Solution
Knowledge Check
A particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .A2u2√3+13g.B4u2√3−19g.C2u2√5−18g.D2u2√3−13g
.A2u2√3+13g.B4u2√3−19g.C2u2√5−18g.D2u2√3−13gA particle is projected from the inclined plane at angle 37∘ with the inclined plane in upward direction with speed 10m/s. The angle of inclined plane with horizontal is 53∘. Then the maximum height attained by the particle from the inclined plane will be-
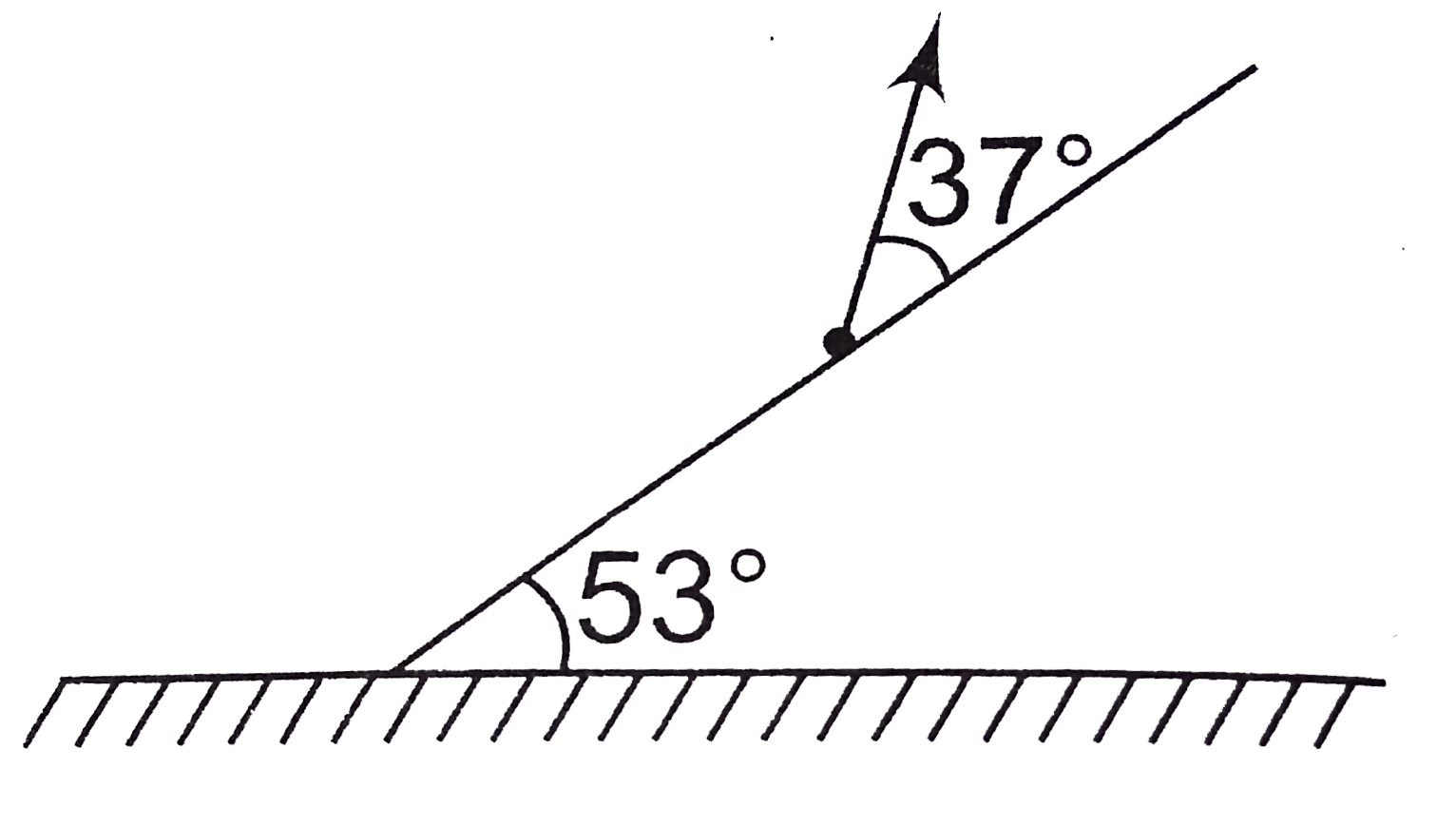 A3mB4mC5mDzero
A3mB4mC5mDzeroA block is projected upwards on a rough inclined plane at 20 m/s. let the time in going up, then is equal to
 A4sB2sC8sD6s
A4sB2sC8sD6s
Two bodies are projected at angle θ and (90%(@) -theta) to the horizontal with the same speed. Find the ration of their time of flight.
View SolutionUpward Projection On An Inclined Plane
View Solution
A particle is projected from surface of the inclined plane with speed u and at an angle θ with the horizontal. After some time the particle collides elastically with the smooth fixed inclined plane for the first time and subsequently moves in vertical direction. Starting from projection, find the time taken by the particle to reach maximum height. (Neglect time of collision).
View SolutionOn an inclined plane two particles AandB are projected with same speed at the same angle with the horizontal, particle A down and particle B up the plane. If the ratio of time of flight of AandB is cotθ, where θ is the angle at which B is projected measured from inclined plane, find the angle at which particles are projected.
View SolutionOn an incliend plane two particles A and B are projected with same speed at the same angle with the horizontal, particle A down and particle B up the plane. If the ratio of time of flight of A and B is cot θ, is the angle at which B is projected measured from. inclined plane, find the angle at which particles are projected.
View Solution

