The ratio of the range of the particle and its maximum range in the inclined plane is:
1:2
1:√2
1:√3
1:1
The correct Answer is:d
R=v0cos30∘T−12gsin30∘T2
=10√32−2√3−12×10×12(2√3)2=203
Rmax=v20g(1+sinθ0)
=10210(1+sinθ0)
=10210(1+sin30∘)=203
So, RRmax=1
Topper's Solved these Questions
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Relative Velocity In Two Dimensions
Explore 23 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Kinematics Of Circular Motion
Explore 26 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Projectile From A Height And Movingframe
Explore 19 Videos
- MOCK TESTBook:A2ZChapter:MOCK TESTExercise:Motion With Constant Acceleration
Explore 15 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Chapter Test
Explore 30 Videos
Similar Questions
The greatest range of a particle projected with a given velocity on an inclined plane is four times the greatest vertical altitude above, the inclined plane.
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘. At what angle α(from the horizontal) should the particle be projected to get the maximum range on the inclined plane.
View Solution
Knowledge Check
A projectile is fired with a velocity v at right angle to the slope inclined at an angle θ with the horizontal. The range of the projectile along the inclined plane is
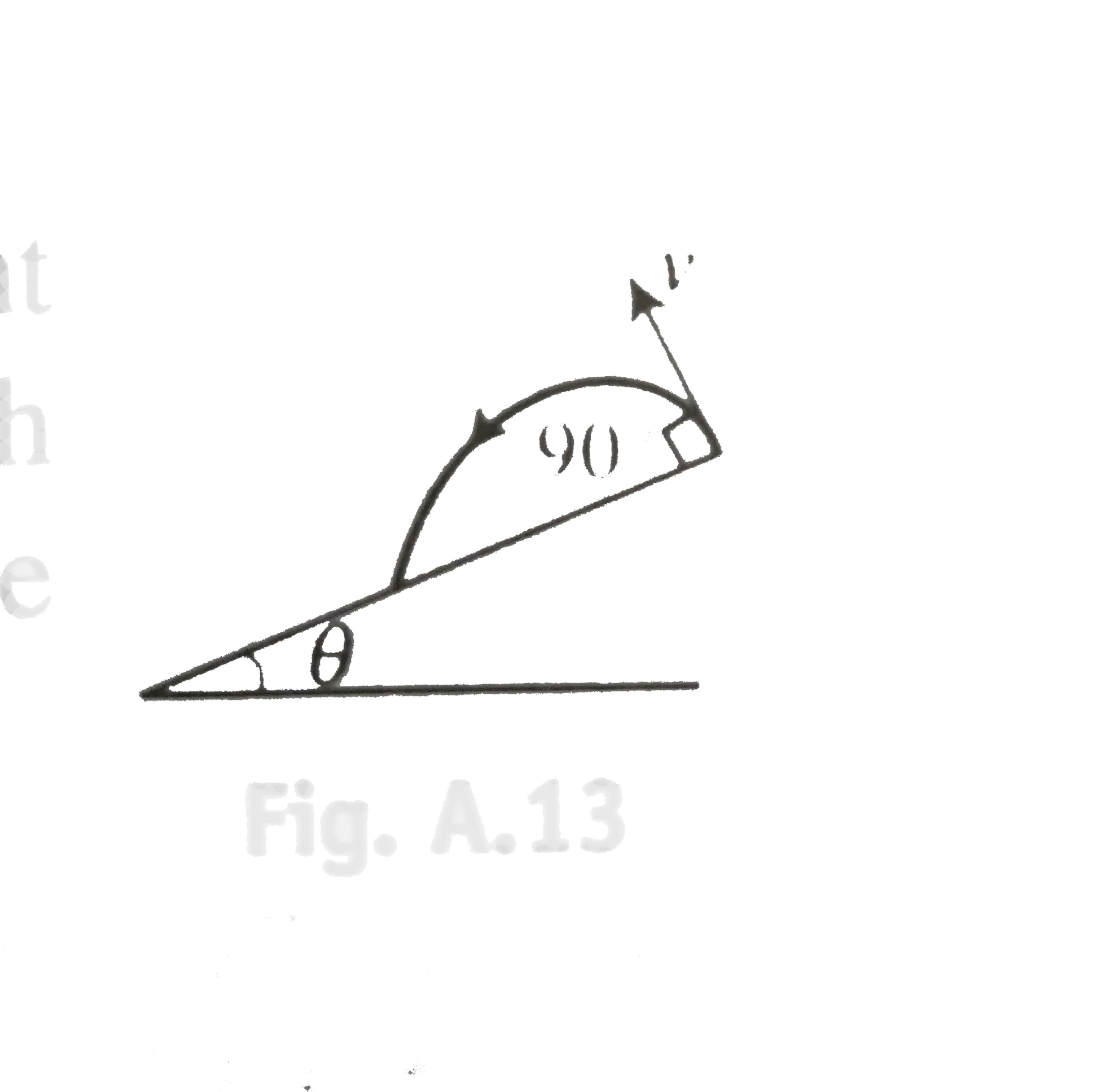 A2v2tanθgBv2secθgC2v2tanθsecθgDv2sinθg
A2v2tanθgBv2secθgC2v2tanθsecθgDv2sinθga particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
A21dmB2.1dmC30dmD6dma particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
A21dmB2.1dmC30dmD6dm
For a given velocity of projection from a point on the inclined plane, the maximum range down the plane is three times the maximum range up the incline. Then find the angle of inclination of the inclined plane.
View SolutionFrom an inclined plane a particleis thrown in a direction normal to the surface. Find the ratio of successive ranges of the particle on inclined plane. Consider all collisions as elastic collisions (particle rebounds with the same speed with which it strikes the plane)
View SolutionA particle is projected at an angle of tan−1(43) with horizontal from a point O.The ratio of the range on the horizontal plane through O to the maximum height ascended above O is
View SolutionThe maximum horizontal range of projectile on the earth is R. Then for the same velocity of projection, its maximum range on another planet is 5R4. Then, ratio of acceleration due to gravity on that planet and on the earth is
View SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .
.
View Solution

