A particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .
.
2u2√3+13g.
4u2√3−19g.
2u2√5−18g.
2u2√3−13g
The correct Answer is:D
R=u2gcos2θ0[sin(2∝+θ0)−sinθ0]
where θ0=30∘and∝=45∘
Then, R=u2gcos230∘[sin(2×45∘+30∘)−sin30∘]
=2u2√3−13g.
Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise 5.3
Explore 12 Videos
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise 5.4
Explore 11 Videos
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise 5.1
Explore 15 Videos
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
A particle is projected along an inclined plane as shown in figure. What is the speed of the particle when it collides at point A ? (g=10m/s)

View SolutionAn inclined plane makes an angle θ0=30∘ with the horizontal. A particle is projected from this plane with a speed of 5ms−1 at an angle of elevation β=30∘ with the horizontal as shown in (Fig. 5.53).
(a) Find the range of the particle on the plane when it strikes the plane.
(b) Find the range of the particle for β=120∘.
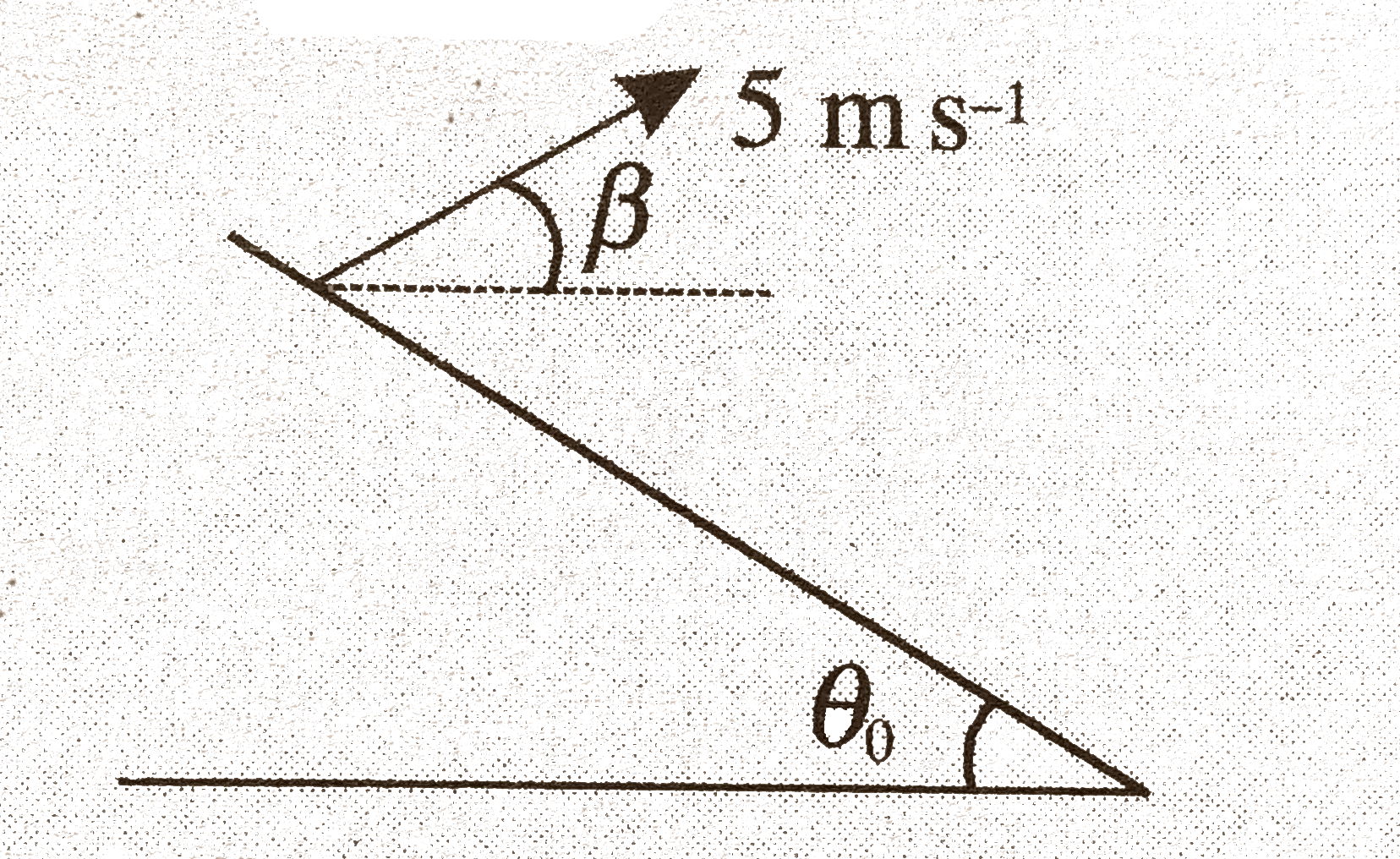 .
.
View Solution
Knowledge Check
a particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
A21dmB2.1dmC30dmD6dma particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
A21dmB2.1dmC30dmD6dmA projectile is projected on an inclined plane as shown in figure. 'D' is a point of maximum height from inclined plane then :
 AAB=BCBAB>BCCBC>ABDtime from A to D is equal to D to C
AAB=BCBAB>BCCBC>ABDtime from A to D is equal to D to C
An particle is projected with velocity u on an inclined plane at an angle θ with the plane. If the particle lands on the plane at right Angle and its time of flight is ucosecθ2g. Find the angle of inclination of the plane with horizontal.
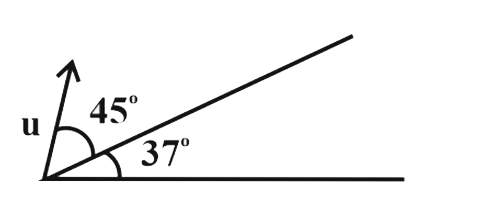
View SolutionA particle is projected on a frictionless inclined plane of inclination 37∘ at an angle of projection 45∘ from the inclined plane as shown in the figure. If after the first collision from the plane, the particle returns to its point of projection, then what is the value of the reciprocal of the coefficient of restitution between the particle and the plane?
View SolutionUpward Projection On An Inclined Plane
View SolutionIf the particle is projected down onto the inclined plane at same speed and angle with the inclined plane the ratio of the time of flight and time of flight for upward projection is :
View Solution
A particle is projected from surface of the inclined plane with speed u and at an angle θ with the horizontal. After some time the particle collides elastically with the smooth fixed inclined plane for the first time and subsequently moves in vertical direction. Starting from projection, find the time taken by the particle to reach maximum height. (Neglect time of collision).
View Solution

