A particle is projected along an inclined plane as shown in figure. What is the speed of the particle when it collides at point A ? (g=10m/s)

The correct Answer is:A, C
T=2usin(α−β)gcosβ
=2×10×sin30∘(10)cos30∘

=2√3s
vx=ux=10cos60∘=5m/s
vy=uy+ayt
=(10sin60∘)+(−10)(2√3)
=5(√3)−20√3=−5√3m/s
=v=(√v2x+v2y)
=(√25+253)
=10√3m/s.
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Single Correct
10 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 More Than One Correct
8 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 1 Single Correct
16 Videos
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
A particle is projected from a tower as shown in figure, then find the distance from the foot of the tower where it will strike the ground. (g=10m/s2)

View SolutionA block is placed on an inclined plane as shown in figure. What must be the friction force between block and inclined if the block is not to slice along the inclined when the incline is accelerating to the right at 3m/s2(sin37∘=35)? (Takeg=10m/s2)
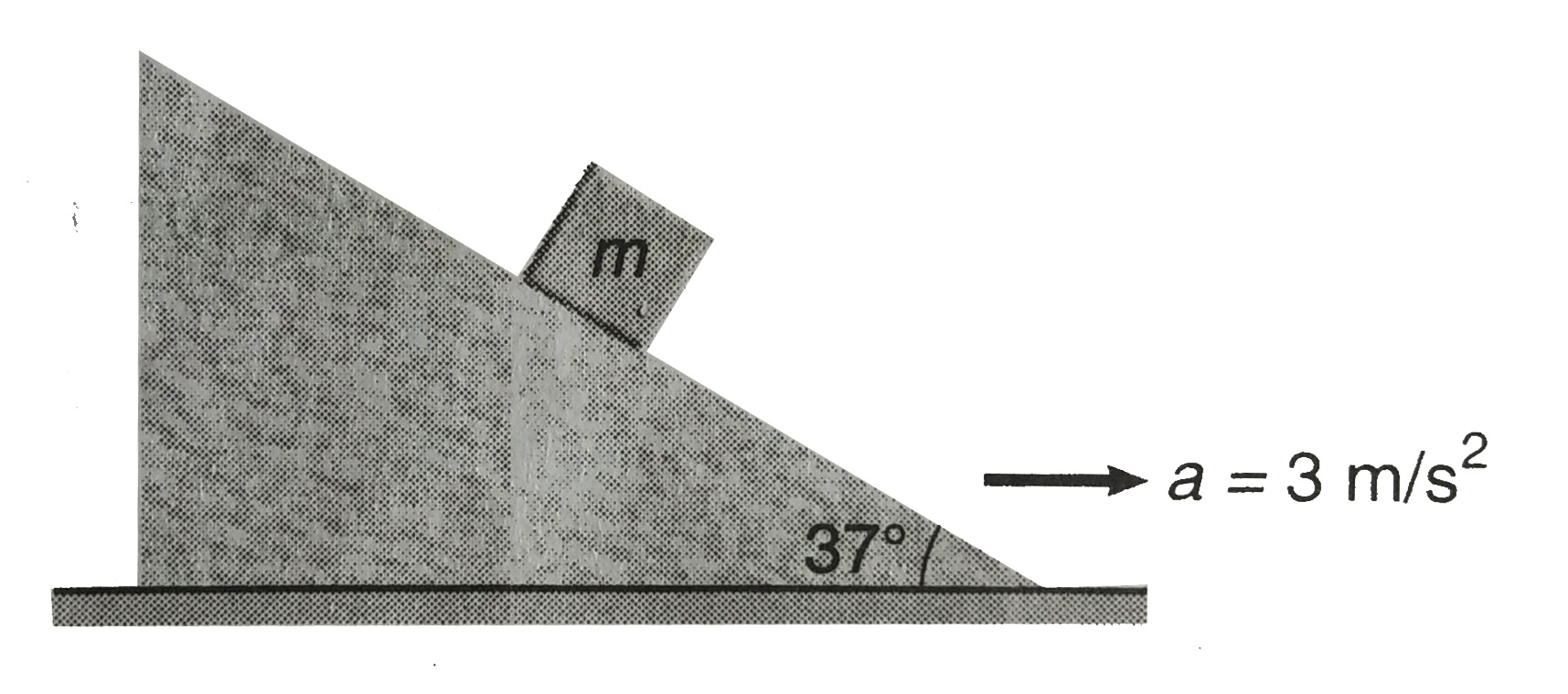
View Solution
Knowledge Check
A projectile is projected on an inclined plane as shown in figure. 'D' is a point of maximum height from inclined plane then :
 AAB=BCBAB>BCCBC>ABDtime from A to D is equal to D to C
AAB=BCBAB>BCCBC>ABDtime from A to D is equal to D to CA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .A2u2√3+13g.B4u2√3−19g.C2u2√5−18g.D2u2√3−13g
.A2u2√3+13g.B4u2√3−19g.C2u2√5−18g.D2u2√3−13gThe speed-time graph of a particle moving along a fixed direction as shown in the figure. The distance travelled by the particle between t = 0 s to t = 10 s is
 A20 mB40 mC60 mD80 m
A20 mB40 mC60 mD80 m
A particle is projected on a frictionless inclined plane of inclination 37∘ at an angle of projection 45∘ from the inclined plane as shown in the figure. If after the first collision from the plane, the particle returns to its point of projection, then what is the value of the reciprocal of the coefficient of restitution between the particle and the plane?
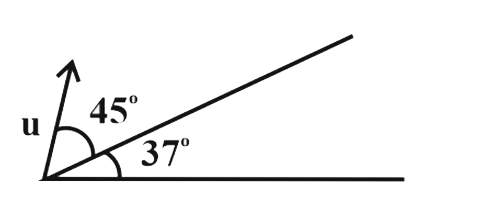
View SolutionThe speed-time graph of a particle moving along a fixed direction is shown in figure. Obtain the distance traversed by the particle between (a)t=0s to 10s(b)t=2s to 6s
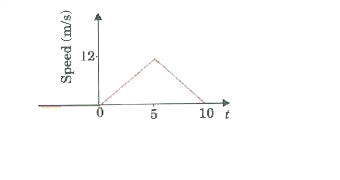
What is the average speed of the particle over the intervals in a and b?
View SolutionA particle is projected with velocity "u" in horizontal direction as shown in the figure. Find u if particle collides perpendicularly with inclined plane. u
View SolutionA particle moves along on a road with constant speed at all points as shown in figure. The normal reaction of the road on the particle is :
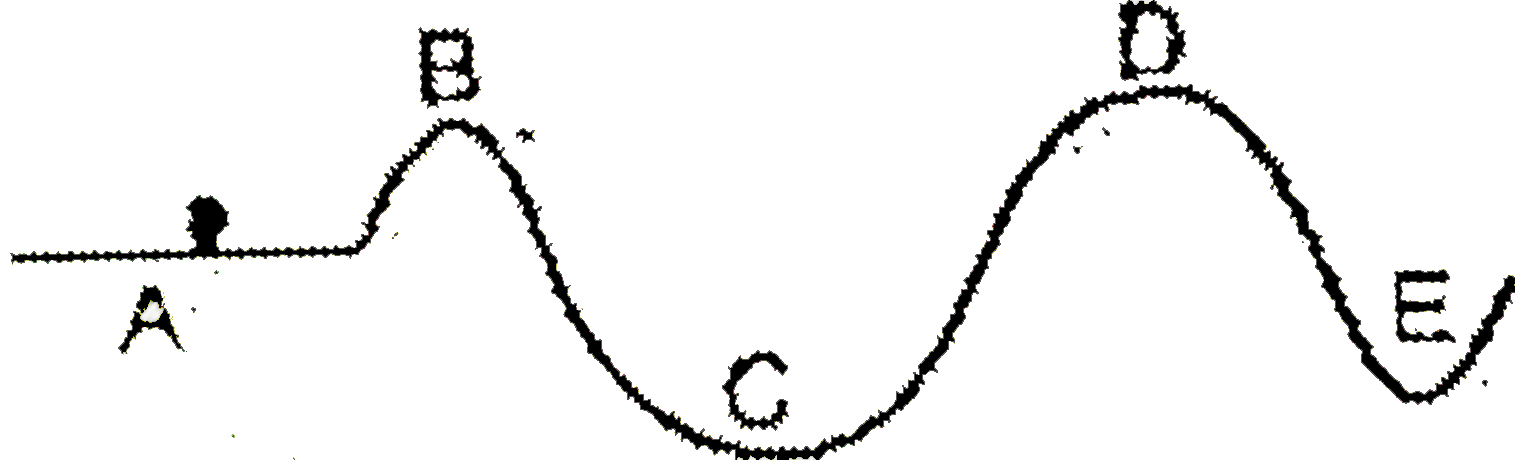
View SolutionA particle is projected at an angle θ from ground with speed u (g = 10 m/s2 )
View Solution
