A particle is projected at an angle θ from ground with speed u (g = 10 m/s2 )
if u = 10 m/s and θ=30∘, then time of flight will be 1 sec
If u=10√3m/sandθ=60∘, then time of flight will be 3 sec.
if u=10√3m/sandθ=60∘, then after 2 sec velocity becomes perpendicular to initial velocity.
if u = 10 m/s and θ=30∘, then velocity never becomes perpendicular to initial velocity during its flight.
The correct Answer is:A, B, C, D
Step by step video, text & image solution for A particle is projected at an angle theta from ground with speed u (g = 10 m/s^2 ) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 3 SUBJECTIVE PROBLEMS (Level-1)
20 Videos
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 3 SUBJECTIVE PROBLEMS (Level-2)
15 Videos
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 2 OBJECTIVE PROBLEMS
75 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM
7 Videos
- KINETIC THEORY OF GASES BOOK - MOTIONCHAPTER - KINETIC THEORY OF GASES EXERCISE - EXERCISE-3 SECTION-B
16 Videos
Similar Questions
A particle is projected at an angle 60∘ with horizontal with a speed v=20m/s. Taking g=10m/s2. Find the time after which the speed of the particle remains half of its initial speed.
View SolutionA particle is projected vertically upwards from ground with an initial speed of 57m/s .If acceleration due to gravity is taken to be equal to 10m/s2 ,then the displacement of the particle in the sixth second of its motion will be?
View Solution
Knowledge Check
A particle is projected at an angle 60∘ with the horizontal with a speed 10m/s. Then, latus rectum is (Take g=10m/s2)
 A5mB15mC10mD0
A5mB15mC10mD0A particle is projected from ground at an angle θ with horizontal with speed u. The ratio of radius of curvature of its trajectory at point of projection to radius of curvature at maximum height is -
A1sin2θcosθBcos2θC1sin3θD1cos3θA particle is projected at angle θ with horizontal from ground. The slop (m) of the trajectory of the particle varies with time (t) as
A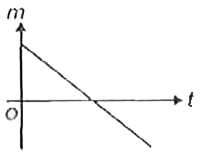 B
B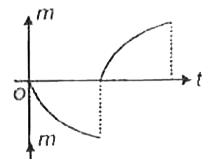 C
C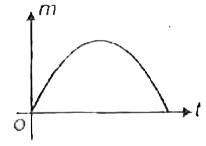 D
D
A particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View SolutionA particle is projected from a point on the ground surface at different angles keeping the speed of projection as constant range obtained is plotted as function of the angle of projection with the horizontal 'O'. Find the range obtained if particle is projected at angle 30° with the horizontal : 2 g 10 m/s 250m R
View SolutionA particle is projected at an angle of θ with the horizontal, with initial speed u.If the magnitude of velocity of projectile motion and time are related as v2−100t2+400t−800=0. Then which of the following is/are correct. (Take g=10m/s2)
View SolutionA particle is projected from horizontal ground at angle 'θ' with speed 'u'. In same plane of motion a horizontal acceleration 'a' exists so that projected particle returns back to point of projection. Find time of flight.
View SolutionA particle is projected from the ground with speed u at angle 60∘ from horizontal. It collides with a second particle of same mass moving with horizontal speed u in same direction at highest point of its trajectory. If collision is perfectly inelastic then find horizontal distance travelled by them after collision when they reached at ground
View Solution
