A particle is thrown horizontally from the top of an inclined plane , with a speed of 5m/s . If the inclination of the plane is 30∘ with the horizontal , how far from the point of projection will the particle strike the plane ?
To solve the problem of finding how far from the point of projection the particle will strike the inclined plane, we can follow these steps:
Step 1: Understand the Geometry of the Problem
We have an inclined plane at an angle of 30∘ with the horizontal. A particle is thrown horizontally with a speed of 5m/s from the top of this incline. We need to determine the horizontal distance d from the point of projection where the particle strikes the plane.
Step 2: Set Up the Coordinate System
Let’s denote:
- x as the horizontal distance traveled by the particle,
- y as the vertical distance fallen by the particle.
From the geometry of the inclined plane, we can relate x and y using the tangent of the angle of inclination:
tan(30∘)=yx
Since tan(30∘)=1√3, we can write:
y=x√3(Equation 1)
Step 3: Analyze the Horizontal Motion
The horizontal motion of the particle is described by the equation:
x=vx⋅t
where vx=5m/s (the horizontal speed) and t is the time of flight. Therefore:
x=5t(Equation 2)
Step 4: Analyze the Vertical Motion
For vertical motion, the particle is under the influence of gravity. The vertical displacement can be given by:
y=0⋅t+12gt2
where g=9.8m/s2. Thus:
y=12gt2(Equation 3)
Step 5: Substitute and Solve for Time
Substituting Equation 2 into Equation 1:
From Equation 1, we have:
y=x√3=5t√3
Now substituting this into Equation 3:
5t√3=12gt2
Rearranging gives:
t2=10tg√3
Dividing both sides by t (assuming t≠0):
t=10g√3
Step 6: Calculate the Horizontal Distance
Now substituting t back into Equation 2 to find x:
x=5t=5⋅10g√3=50g√3
Substituting g=9.8m/s2:
x=509.8√3≈5016.97≈2.95m
Step 7: Calculate the Vertical Distance
Using t in Equation 3 to find y:
y=12gt2=12⋅9.8⋅(109.8√3)2=12⋅9.8⋅100(9.82⋅3)=503⋅9.8≈1.70m
Step 8: Calculate the Distance from the Point of Projection
Using the Pythagorean theorem to find the distance d:
d=√x2+y2=√(2.95)2+(1.70)2≈√8.7025+2.89≈√11.5925≈3.41m
Final Answer
The particle will strike the inclined plane approximately 3.41 meters from the point of projection.
---
We have an inclined plane at an angle of 30∘ with the horizontal. A particle is thrown horizontally with a speed of 5m/s from the top of this incline. We need to determine the horizontal distance d from the point of projection where the particle strikes the plane.
Let’s denote:
- x as the horizontal distance traveled by the particle,
- y as the vertical distance fallen by the particle.
tan(30∘)=yx
Since tan(30∘)=1√3, we can write:
y=x√3(Equation 1)
The horizontal motion of the particle is described by the equation:
x=vx⋅t
where vx=5m/s (the horizontal speed) and t is the time of flight. Therefore:
x=5t(Equation 2)
For vertical motion, the particle is under the influence of gravity. The vertical displacement can be given by:
y=0⋅t+12gt2
where g=9.8m/s2. Thus:
y=12gt2(Equation 3)
Substituting Equation 2 into Equation 1:
From Equation 1, we have:
y=x√3=5t√3
Now substituting this into Equation 3:
5t√3=12gt2
Rearranging gives:
t2=10tg√3
Dividing both sides by t (assuming t≠0):
t=10g√3
Now substituting t back into Equation 2 to find x:
x=5t=5⋅10g√3=50g√3
Substituting g=9.8m/s2:
x=509.8√3≈5016.97≈2.95m
Using t in Equation 3 to find y:
y=12gt2=12⋅9.8⋅(109.8√3)2=12⋅9.8⋅100(9.82⋅3)=503⋅9.8≈1.70m
Using the Pythagorean theorem to find the distance d:
d=√x2+y2=√(2.95)2+(1.70)2≈√8.7025+2.89≈√11.5925≈3.41m
The particle will strike the inclined plane approximately 3.41 meters from the point of projection.
Topper's Solved these Questions
- MOTION IN A PLANE Book:MODERN PUBLICATIONChapter:MOTION IN A PLANE Exercise:PRACTICE PROBLEMS (1)
Explore 8 Videos
- MOTION IN A PLANE Book:MODERN PUBLICATIONChapter:MOTION IN A PLANE Exercise:PRACTICE PROBLEMS (2)
Explore 9 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:MODERN PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Chapter Practise Test
Explore 16 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:CHAPTER PRACTICE TEST
Explore 16 Videos
Similar Questions
A particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle is projected horizontal with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane?
View Solution
Knowledge Check
A ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
A2v2gB√2[2v2g]Cv2gD√2v2gA particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle θ=37∘ to the horizontal (g=10m/s2)

How far from the point of projection will the particle strike the plane?A75mB6516mC7516mD859mA particle of mass m is thrown horizontally from point P , as shown in the figure, with speed 5m/s. It strikes an inclined plane perpendicularly as shown. The inclination of the plane is 30∘ with the horizontal. Then, the height h shown in the figure is ( Take g=10m/s2 ) .
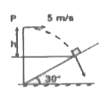 A3.75mB5.0mC4.75mD0.417m
A3.75mB5.0mC4.75mD0.417m
A pariicle is projected horizontally with a speed (u) from top of a plance inclined at anangle θ with the horizontal direction. How far from the point of projection will the particle strike the plane ?
View SolutionA particles is projected horizontally with a speed v from the top of a plane inclined at an angle tehta to the horizontal as shown in the figure.
(a) Hwo far from the point of projection will the particle strike the plane ?
(b) Find the time taken by the particel to hit the plane.
(c) What is the velocity of particle just before it hits the plane ?
View SolutionAn inclined plane makes an angle θ0=30∘ with the horizontal. A particle is projected from this plane with a speed of 5ms−1 at an angle of elevation β=30∘ with the horizontal as shown in (Fig. 5.53).
(a) Find the range of the particle on the plane when it strikes the plane.
(b) Find the range of the particle for β=120∘.
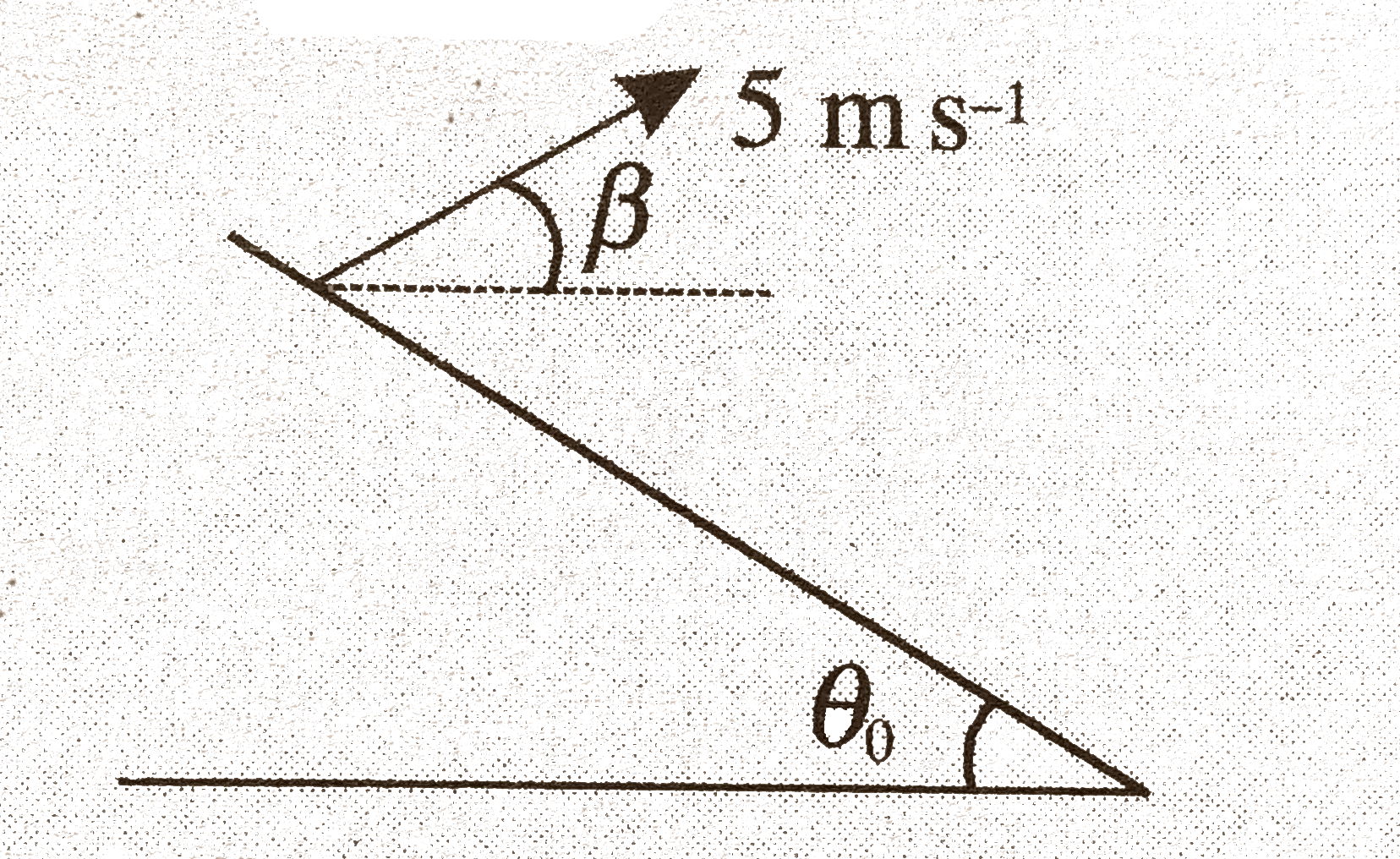 .
.
View SolutionA particle is thrown horizontally with velocity 10 m/s from an incline of inclination 30∘ , it hits on the incline agin then displacement (in m) of the particle is:
View SolutionA particle is projected with a velocity u from the foot of an inclined plane whose inclination to the horizon is β. It strikes. the plane at right angles if
View Solution