If the velocity of a particle is , where and are constant, then the distance travelled by it between and is :
The correct Answer is:B
To solve the problem, we need to find the distance traveled by a particle with a given velocity function v(t)=At+Bt2 between t=1 second and t=2 seconds.
1. Understand the relationship between velocity and displacement:
The velocity v is defined as the derivative of displacement x with respect to time t:
v=dxdt
Therefore, we can write:
dxdt=At+Bt2
2. Rearrange the equation:
We can rearrange this to express dx:
dx=(At+Bt2)dt
3. Set up the integral for displacement:
To find the total displacement Δx between t=1 s and t=2 s, we integrate dx from t=1 to t=2:
Δx=∫21(At+Bt2)dt
4. Break down the integral:
We can split the integral into two parts:
Δx=∫21Atdt+∫21Bt2dt
5. Calculate the first integral:
The first integral is:
∫Atdt=A2t2∣∣21=A2(22−12)=A2(4−1)=3A2
6. Calculate the second integral:
The second integral is:
∫Bt2dt=B3t3∣∣21=B3(23−13)=B3(8−1)=7B3
7. Combine the results:
Now, we can combine both results to find the total displacement:
Δx=3A2+7B3
8. Final expression:
Thus, the distance traveled by the particle between t=1 s and t=2 s is:
Δx=3A2+7B3
The velocity v is defined as the derivative of displacement x with respect to time t:
v=dxdt
Therefore, we can write:
dxdt=At+Bt2
We can rearrange this to express dx:
dx=(At+Bt2)dt
To find the total displacement Δx between t=1 s and t=2 s, we integrate dx from t=1 to t=2:
Δx=∫21(At+Bt2)dt
We can split the integral into two parts:
Δx=∫21Atdt+∫21Bt2dt
The first integral is:
∫Atdt=A2t2∣∣21=A2(22−12)=A2(4−1)=3A2
The second integral is:
∫Bt2dt=B3t3∣∣21=B3(23−13)=B3(8−1)=7B3
Now, we can combine both results to find the total displacement:
Δx=3A2+7B3
Thus, the distance traveled by the particle between t=1 s and t=2 s is:
Δx=3A2+7B3
Topper's Solved these Questions
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:(B) Meical entrance special format questions (Mathch the columns)
Explore 6 Videos
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:Medical entrances gallery
Explore 19 Videos
- PROJECTILE MOTIONBook:DC PANDEY ENGLISHChapter:PROJECTILE MOTIONExercise:Level - 2 Subjective
Explore 10 Videos
Similar Questions
If xy=a2andS=b2x+c2y where a,bandc are constants then the minimum value of S is
View SolutionThe position of a particle is given by
x=2(t−t2)
where t is expressed in seconds and x is in metre.
The total distance travelled by the paticle between t=0 to t=1s is
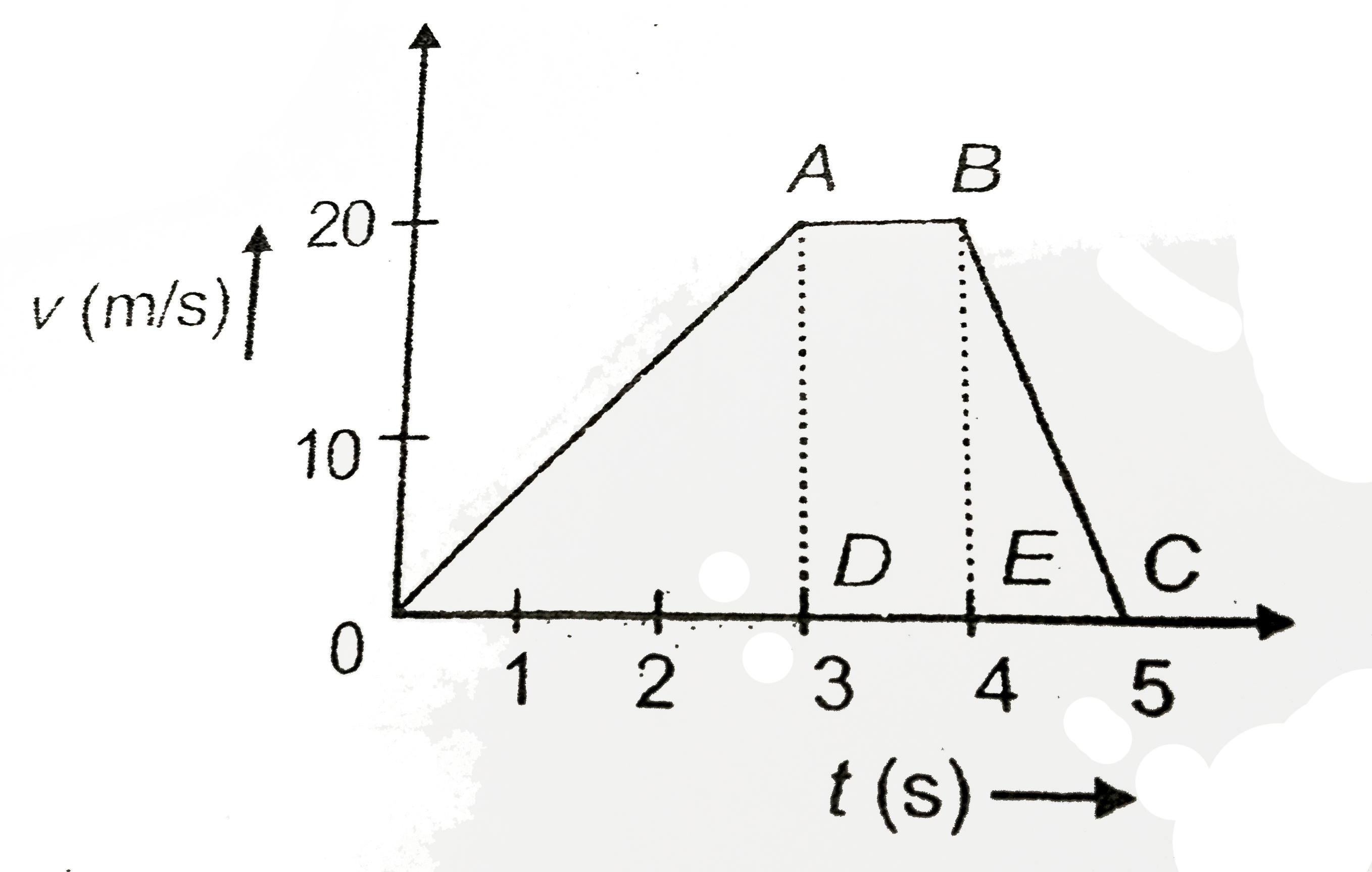
View SolutionThe variation of velocity of a particle moving along a straight line is as shown in the figure given below. The distance travelled by the particle in 5 s is
View SolutionThe position (in meters) of a particle moving on the x-axis is given by: x=2+9t+3t2−t3, where t is time in seconds . The distance travelled by the particle between t= 1s and t= 4s is m.
View SolutionThe momentum of a particle is P=A+Bt2 . Where , A and B are constant perpendicular vectors . The force acting on the particle when its acceleration is at 45∘ with its velocity is
(a)2√ABB (b)2B (c)zero (d)2A
View SolutionThe variation of velocity of a particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4s is
View SolutionThe period of a particle in SHM is 8s. At t=0 it is in its equilibrium position.
(a) Compare the distance travelled in the first 4s and the second 4s.
(b) Compare the distance travelled in the first 2s and the second 2s.
View SolutionIf velocity of a particle is given by v=(2t+3)m/s. Then average velocity in interval 0≤t≤1 s is :
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :
View SolutionVelocity of a particle is given as v=(2t2−3)m/s. The acceleration of particle at t = 3s will be :
View Solution