A point moving with constant acceleration from A to B in the straight line AB has velocities u and v at A and B respectively. Find its velocity at C, the mid point of AB. Also show that if the time from A to C is twice that from C to B, then v=7u.
5 u
6 u
7 u
8 u
The correct Answer is:C
To solve the problem step by step, we will follow the concepts of kinematics, particularly focusing on the equations of motion under constant acceleration.
Step 1: Define the problem
We have a point moving with constant acceleration from point A to point B. The initial velocity at A is u and the final velocity at B is v. We need to find the velocity at point C, which is the midpoint of AB.
Step 2: Identify the distances
Let the total distance AB=L. Therefore, the distance from A to C (the midpoint) is L2, and the distance from C to B is also L2.
Step 3: Use the equation of motion
Using the third equation of motion, we can express the relationship between the velocities and the distance. For point C, we can write:
v2C−u2=2a(L2)
where vC is the velocity at point C and a is the acceleration.
Step 4: Rearranging the equation
From the equation above, we can simplify it to:
v2C−u2=aL
This gives us:
v2C=u2+aL
Step 5: Relate acceleration to velocities
Using the first equation of motion for the entire distance from A to B, we have:
v2−u2=2aL
From this, we can express aL as:
aL=v2−u22
Step 6: Substitute aL back into the equation for v2C
Substituting aL into the equation for v2C:
v2C=u2+v2−u22
This simplifies to:
v2C=2u2+v2−u22=u2+v22
Thus, we have:
vC=√u2+v22
Step 7: Analyze the time relationship
According to the problem, the time taken from A to C is twice that from C to B. Let the time from C to B be t. Thus, the time from A to C is 2t.
Step 8: Write the distance equations
For the distance from A to C:
L2=u(2t)+12a(2t)2
This simplifies to:
L2=2ut+2at2
For the distance from C to B:
L2=vCt+12at2
Step 9: Substitute vC into the second equation
Substituting vC=√u2+v22:
L2=√u2+v22t+12at2
Step 10: Solve for v
Now, we have two equations:
1. L=4ut+4at2 (from A to C)
2. L=2√u2+v22t+at2 (from C to B)
Equating these two expressions for L and solving for v leads us to the conclusion that v=7u.
Final Result
Thus, the velocity at point C is given by:
vC=√u2+v22
And if the time from A to C is twice that from C to B, we find that:
v=7u
We have a point moving with constant acceleration from point A to point B. The initial velocity at A is u and the final velocity at B is v. We need to find the velocity at point C, which is the midpoint of AB.
Let the total distance AB=L. Therefore, the distance from A to C (the midpoint) is L2, and the distance from C to B is also L2.
Using the third equation of motion, we can express the relationship between the velocities and the distance. For point C, we can write:
v2C−u2=2a(L2)
where vC is the velocity at point C and a is the acceleration.
From the equation above, we can simplify it to:
v2C−u2=aL
This gives us:
v2C=u2+aL
Using the first equation of motion for the entire distance from A to B, we have:
v2−u2=2aL
From this, we can express aL as:
aL=v2−u22
Substituting aL into the equation for v2C:
v2C=u2+v2−u22
This simplifies to:
v2C=2u2+v2−u22=u2+v22
Thus, we have:
vC=√u2+v22
According to the problem, the time taken from A to C is twice that from C to B. Let the time from C to B be t. Thus, the time from A to C is 2t.
For the distance from A to C:
L2=u(2t)+12a(2t)2
This simplifies to:
L2=2ut+2at2
For the distance from C to B:
L2=vCt+12at2
Substituting vC=√u2+v22:
L2=√u2+v22t+12at2
Now, we have two equations:
1. L=4ut+4at2 (from A to C)
2. L=2√u2+v22t+at2 (from C to B)
Thus, the velocity at point C is given by:
vC=√u2+v22
And if the time from A to C is twice that from C to B, we find that:
v=7u
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Mathch the columns)
6 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery
19 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
Similar Questions
A body is moving with constant acceleration, a=5ms2 from A to B in straight line AB. The velocity of particle at A and B are 5 m/s and 15 m/s respectively. The velocity at mid-point of AB is
View SolutionA particle moving with uniform acceleration from A to B along a straight line has velcities v1 and v2 at A and B respectively. If C is the mid-point between A and B then determine the velocity of the particle at C .
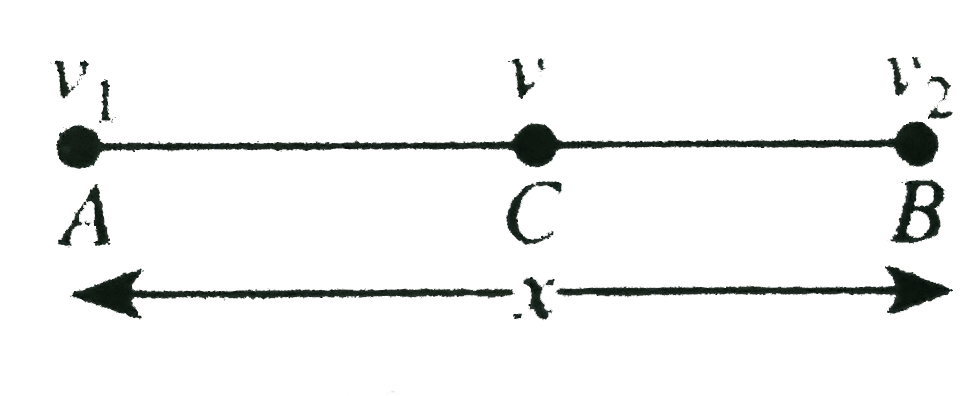 .
.
View SolutionA particle is moving with uniform acceleration along a straight line. Its velocities at A & B are respectively 7m/s & 17m/s. M is mid point of AB. If t1 is the time taken to go from A to M and t2 the time taken to go from M to B, the ratio t1t2 is equal to :-
View SolutionA particle moving along a straight line with uniform acceleration has velocities 7m/s at A and 17m/s at C. B is the mid point of AC. Then :-
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the
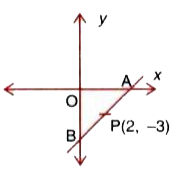
slope of line AB
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the
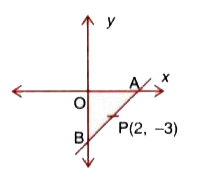
equation of line AB.
View SolutionThe two ends of a train moving with uniform acceleration pass a certain point with velocity u and v. Find the velocity with which the middle point of the train passes the same point.
View SolutionA straight line through the point (1,1) meets the X-axis at A and Y-axis at B. The locus of the mid-point of AB is
View SolutionThe coordinatse of two points A and B are (−1,4)and(5,1), respectively. Find the coordinates of the point P which lie on extended line AB such that it is three times as far from B as from A.
View SolutionA stone thrown vertically up with velocity v reaches three points A, B and C with velocities v,v2 and v4 respectively. Then AB:BC is
View Solution
