A and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the
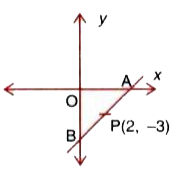
slope of line AB
The correct Answer is:
Step by step video, text & image solution for A and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the slope of line AB by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- EQUATION OF A LINEBook:ICSEChapter:EQUATION OF A LINEExercise:EXERCISE 14(D)
Explore 41 Videos
- CYLINDER, CONE AND SPHERE Book:ICSEChapter:CYLINDER, CONE AND SPHERE Exercise:EXERCISE 20 (G)
Explore 23 Videos
- FACTORISATIONBook:ICSEChapter:FACTORISATIONExercise:M.C.Q(Competency Based Questions )
Explore 15 Videos
Similar Questions
A and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the
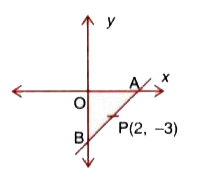
equation of line AB.
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the
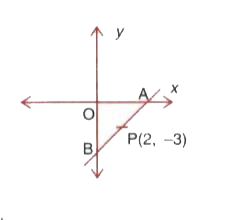
co-ordinates of A and B.
View SolutionM and N are two points on the X-axis and Y-axis respectively. P(3, 2) divides the line segment MN in the ratio 2:3.
Find :
slope of the line MN.
View SolutionM and N are two points on the X-axis and Y-axis respectively. P(3, 2) divides the line segment MN in the ratio 2:3.
Find :
(i) the coordinates of M and N
View SolutionA line intersects the y-axis and x-axis at the points P and Q respectively. If (2, 5) is the mid-point of PQ, then find the coordinates of P and Q.
View SolutionA line intersects the Y- axis and X-axis at the points P and Q, respectively. If (2,-5) is the mid- point of PQ, then the coordinates of P and Q are, respectively.
View SolutionPoints A and B have co-ordinates (3, 5) and (x, y) respectively. The mid-point of AB is (2, 3). Find the values of x and y.
View SolutionThe line xa+yb=1 meets the axis of and y at A and B respectively and C is middle point of AB then
View SolutionLet y=f(x) be a curve passing through (4,3) such that slope of normal at any point lying in the first quadrant is negative and the normal and tangent at any point P cuts the Y-axis at A and B respectively such that the mid-point of AB is origin, then the number of solutions of y=f(x) and f=|5−|x∣∣, is
View SolutionSuppose A, B are two points on 2x−y+3=0andP(1,2) is such that PA=PB. Then the mid point of AB is
View Solution

