A line intersects the Y- axis and X-axis at the points P and Q, respectively. If (2,-5) is the mid- point of PQ, then the coordinates of P and Q are, respectively.
(0,-5) and (2,0)
(0,10) and (-4,0)
(0,4) and (-10, 0)
(0,-10) and (4,0)
The correct Answer is:D
To find the coordinates of points P and Q where a line intersects the Y-axis and X-axis respectively, given that (2, -5) is the midpoint of PQ, we can follow these steps:
Step 1: Define the Points
Let the coordinates of point P (where the line intersects the Y-axis) be (0, y1) and the coordinates of point Q (where the line intersects the X-axis) be (x2, 0).
Step 2: Use the Midpoint Formula
The midpoint M of a line segment connecting two points (x1, y1) and (x2, y2) is given by:
M=(x1+x22,y1+y22)
In our case, the midpoint M is given as (2, -5). Therefore, we can set up the following equations:
0+x22=2(1)
y1+02=−5(2)
Step 3: Solve for x2
From equation (1):
x22=2
Multiplying both sides by 2 gives:
x2=4
Step 4: Solve for y1
From equation (2):
y12=−5
Multiplying both sides by 2 gives:
y1=−10
Step 5: Write the Coordinates of P and Q
Now we can write the coordinates of points P and Q:
- Point P (0, y1) = (0, -10)
- Point Q (x2, 0) = (4, 0)
Conclusion
Thus, the coordinates of points P and Q are:
- P = (0, -10)
- Q = (4, 0)
Let the coordinates of point P (where the line intersects the Y-axis) be (0, y1) and the coordinates of point Q (where the line intersects the X-axis) be (x2, 0).
The midpoint M of a line segment connecting two points (x1, y1) and (x2, y2) is given by:
M=(x1+x22,y1+y22)
In our case, the midpoint M is given as (2, -5). Therefore, we can set up the following equations:
0+x22=2(1)
y1+02=−5(2)
From equation (1):
x22=2
Multiplying both sides by 2 gives:
x2=4
From equation (2):
y12=−5
Multiplying both sides by 2 gives:
y1=−10
Now we can write the coordinates of points P and Q:
- Point P (0, y1) = (0, -10)
- Point Q (x2, 0) = (4, 0)
Thus, the coordinates of points P and Q are:
- P = (0, -10)
- Q = (4, 0)
Topper's Solved these Questions
- COORDINATE GEOMETRYBook:NCERT EXEMPLAR ENGLISHChapter:COORDINATE GEOMETRYExercise:Exercise 7.2 Very Short Answer Type Questions
Explore 12 Videos
- COORDINATE GEOMETRYBook:NCERT EXEMPLAR ENGLISHChapter:COORDINATE GEOMETRYExercise:Exercise 7.3 Very Short Answer Type Questions
Explore 20 Videos
- CONSTRUCTIONSBook:NCERT EXEMPLAR ENGLISHChapter:CONSTRUCTIONSExercise:Exercise 10.4 Long Answer type Questions
Explore 7 Videos
- INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONSBook:NCERT EXEMPLAR ENGLISHChapter:INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONSExercise:LONG ANSWER TYPES QUESTIONS
Explore 18 Videos
Similar Questions
A line intersects the y-axis and x-axis at the points P and Q respectively. If (2, 5) is the mid-point of PQ, then find the coordinates of P and Q.
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the

co-ordinates of A and B.
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the
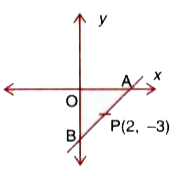
slope of line AB
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the

equation of line AB.
View SolutionLet a line xa+yb=1 intersects the x-axis at A and y-axis at B resapectively. A line parallel to it is drawn to intersect the axes in P and Q respectively. The extermities of the lines are joined transversely. If the locus of point of intersection of the line joining them is xa=cyb, then c is equal to
View SolutionThe line segment joining the points (3, −4) and (1, 2) is trisected at the points P and Q . If the coordinates of P and Q are (p, −2) and (5/3, q) respectively. Find the values of p and q .
View SolutionM and N are two points on the X-axis and Y-axis respectively. P(3, 2) divides the line segment MN in the ratio 2:3.
Find :
(i) the coordinates of M and N
View SolutionThe line 4x−7y+10=0 intersects the parabola y2=4x at the points P and Q. The coordinates of the point of intersection of the tangents drawn at the points P and Q are
View SolutionP and Q have co-ordinates (-2, 3) and (5, 4) respectively. Reflect P in the x-axis to P' and Q in the y-axis to Q'. State the co-ordinates of P' and 'Q .
View SolutionTwo lines cut on the axis of x intercepts 4and−4 and on the axis of y intercepts 2 and 6 respectively. Find the coordinates of their point of intersection.
View Solution