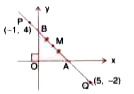
A straight line passes through the points P(−1,4) and Q(5,−2). It intersects x-axis at point A and y-axis at point B. M is the midpoint of the line segment AB. Find :
the co-ordinates of point M.
The correct Answer is:(32,32)
To find the coordinates of point M, the midpoint of the line segment AB, we will follow these steps:
Step 1: Find the slope of the line passing through points P and Q.
The slope (m) of a line passing through two points (x1,y1) and (x2,y2) is given by the formula:
m=y2−y1x2−x1
For points P(−1,4) and Q(5,−2):
- x1=−1, y1=4
- x2=5, y2=−2
Substituting the values:
m=−2−45−(−1)=−66=−1
Step 2: Use the slope-point form to find the equation of the line.
The slope-point form of the equation of a line is:
y−y1=m(x−x1)
Using point P(-1, 4) and the slope m=−1:
y−4=−1(x+1)
Simplifying this:
y−4=−x−1⟹y+x=3
Step 3: Find the x-intercept (point A).
To find the x-intercept, set y=0 in the equation y+x=3:
0+x=3⟹x=3
So, point A is (3,0).
Step 4: Find the y-intercept (point B).
To find the y-intercept, set x=0 in the equation y+x=3:
y+0=3⟹y=3
So, point B is (0,3).
Step 5: Find the midpoint M of line segment AB.
The midpoint M of a line segment connecting points A (x1,y1) and B (x2,y2) is given by:
M=(x1+x22,y1+y22)
Substituting the coordinates of points A and B:
- A = (3, 0)
- B = (0, 3)
Calculating the midpoint:
M=(3+02,0+32)=(32,32)
Final Answer:
The coordinates of point M are (32,32).
---
The slope (m) of a line passing through two points (x1,y1) and (x2,y2) is given by the formula:
m=y2−y1x2−x1
For points P(−1,4) and Q(5,−2):
- x1=−1, y1=4
- x2=5, y2=−2
m=−2−45−(−1)=−66=−1
The slope-point form of the equation of a line is:
y−y1=m(x−x1)
Using point P(-1, 4) and the slope m=−1:
y−4=−1(x+1)
Simplifying this:
y−4=−x−1⟹y+x=3
To find the x-intercept, set y=0 in the equation y+x=3:
0+x=3⟹x=3
So, point A is (3,0).
To find the y-intercept, set x=0 in the equation y+x=3:
y+0=3⟹y=3
So, point B is (0,3).
The midpoint M of a line segment connecting points A (x1,y1) and B (x2,y2) is given by:
M=(x1+x22,y1+y22)
Substituting the coordinates of points A and B:
- A = (3, 0)
- B = (0, 3)
M=(3+02,0+32)=(32,32)
The coordinates of point M are (32,32).
Topper's Solved these Questions
- EQUATION OF A LINEBook:ICSEChapter:EQUATION OF A LINEExercise:EXERCISE 14(D)
Explore 41 Videos
- CYLINDER, CONE AND SPHERE Book:ICSEChapter:CYLINDER, CONE AND SPHERE Exercise:EXERCISE 20 (G)
Explore 23 Videos
- FACTORISATIONBook:ICSEChapter:FACTORISATIONExercise:M.C.Q(Competency Based Questions )
Explore 15 Videos
Similar Questions
A straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
The co-ordinates of A and B.
View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
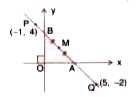
The co-ordinates of M.
View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :

The equation of the line.
View SolutionA straight line passes through the points A(-5, 2) and B(3,-6). It intersects the co-ordinate axes at points C and D . Find :
the equation of AB.
View SolutionA straight line passes through the points A(-5, 2) and B(3,6). It intersects the co-ordinate axes at points C and D . M is a point on AB which divides CD in the ratio 1: 2. Find :
the co-ordinates of point M.
View SolutionA straight line passes through the points A(-5, 2) and B(3,6). It intersects the co-ordinate axes at points C and D . M is a point on AB which divides CD in the ratio 1: 2. Find :
the co-ordinates of points C and D.
View SolutionIn the given figure, P (4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
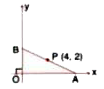
View SolutionFind the equation of a line passing through the points (7,−3)and(2,−2). If this line meets x-axis at point P and y-axis at point Q, find the co-ordinates of points P and Q.
View SolutionA straight line passes through the point P(3, 2). It meets the x-axis at point A and the y-axis at point B. If PAPB=23. find the equation of the line that passes through the point P and is perpendicular to line AB.
View SolutionThe line 3x - 4y + 12 = 0 meets x-axis at point A and y-axis at point B. Find :
the co-ordinates of A and B.
View Solution

