A projectile takes off with an initial velocity of 50m//s at an angle of 37∘ with horizontal, It is just able to clear two hurdles of height 25m each, separated from each other by a distance d Calculate d.
160m
50m
320m
40m
The correct Answer is:A
To solve the problem of finding the distance d between two hurdles that a projectile just clears, we can break down the solution into several steps.
1. Identify the Components of Initial Velocity:
The projectile is launched with an initial velocity u=50m/s at an angle θ=37∘.
- The horizontal component of the velocity ux is given by:
ux=ucos(θ)=50cos(37∘)=50×45=40m/s
- The vertical component of the velocity uy is given by:
uy=usin(θ)=50sin(37∘)=50×35=30m/s
2. Use the Second Equation of Motion for Vertical Displacement:
The height of the hurdles is h=25m. We can use the second equation of motion to find the time t when the projectile reaches this height:
h=uyt−12gt2
where g is the acceleration due to gravity (approximately 10m/s2).
Substituting the values:
25=30t−12⋅10⋅t2
Simplifying gives:
25=30t−5t2
Rearranging this into standard quadratic form:
5t2−30t+25=0
Dividing the entire equation by 5:
t2−6t+5=0
3. Solve the Quadratic Equation:
We can factor this quadratic equation:
(t−1)(t−5)=0
Thus, the solutions for t are:
t1=1sandt2=5s
4. Calculate the Distance d:
The horizontal distance d between the two hurdles can be calculated using the horizontal velocity:
d=ux(t2−t1)=40m/s×(5s−1s)=40×4=160m
Final Answer:
The distance d between the two hurdles is 160m.
---
The projectile is launched with an initial velocity u=50m/s at an angle θ=37∘.
- The horizontal component of the velocity ux is given by:
ux=ucos(θ)=50cos(37∘)=50×45=40m/s
- The vertical component of the velocity uy is given by:
uy=usin(θ)=50sin(37∘)=50×35=30m/s
The height of the hurdles is h=25m. We can use the second equation of motion to find the time t when the projectile reaches this height:
h=uyt−12gt2
where g is the acceleration due to gravity (approximately 10m/s2).
Substituting the values:
25=30t−12⋅10⋅t2
Simplifying gives:
25=30t−5t2
Rearranging this into standard quadratic form:
5t2−30t+25=0
Dividing the entire equation by 5:
t2−6t+5=0
We can factor this quadratic equation:
(t−1)(t−5)=0
Thus, the solutions for t are:
t1=1sandt2=5s
The horizontal distance d between the two hurdles can be calculated using the horizontal velocity:
d=ux(t2−t1)=40m/s×(5s−1s)=40×4=160m
The distance d between the two hurdles is 160m.
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Video
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
A projectile takes off with an initial velocity of 10m/s at an angle of elevation of 45∘. It is just able to clear two hurdles of height 2 m each, separated from each other by a distance d. Calculate d. At what distance from the point of projection is the first hurdle placed? Take g=10m/s2.
View SolutionA projectile projected with initial velocity 20m/s and at and angle of 30∘ from horizontal. Find the total work done when it will hit the ground.
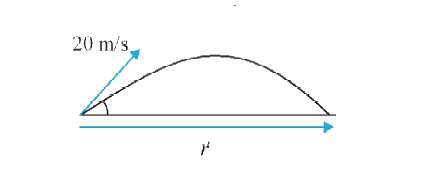
View Solution
Knowledge Check
A ball is thrown from the top of a tower with an initial velocity of 10m/s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
A5 mB20 mC15 mD10 m
A particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA ball is thrown from the top of a tower with an intial velocity of 10 m//s at an angle 37∘ above the horizontal, hits the ground at a distance 16 m from the base of tower. Calculate height of tower. [g=10m/s2]
View SolutionWhat is the range of a projectile thrown with velocity 98m/s with angle 30∘ from horizontal ?
View SolutionA particle A is projected with an initial velocity of 60m/s at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a)the angle of projection α of particle B, (b) time when the collision takes place and (c) the distance of P from A, where collision occurs. (g=10m/s2)
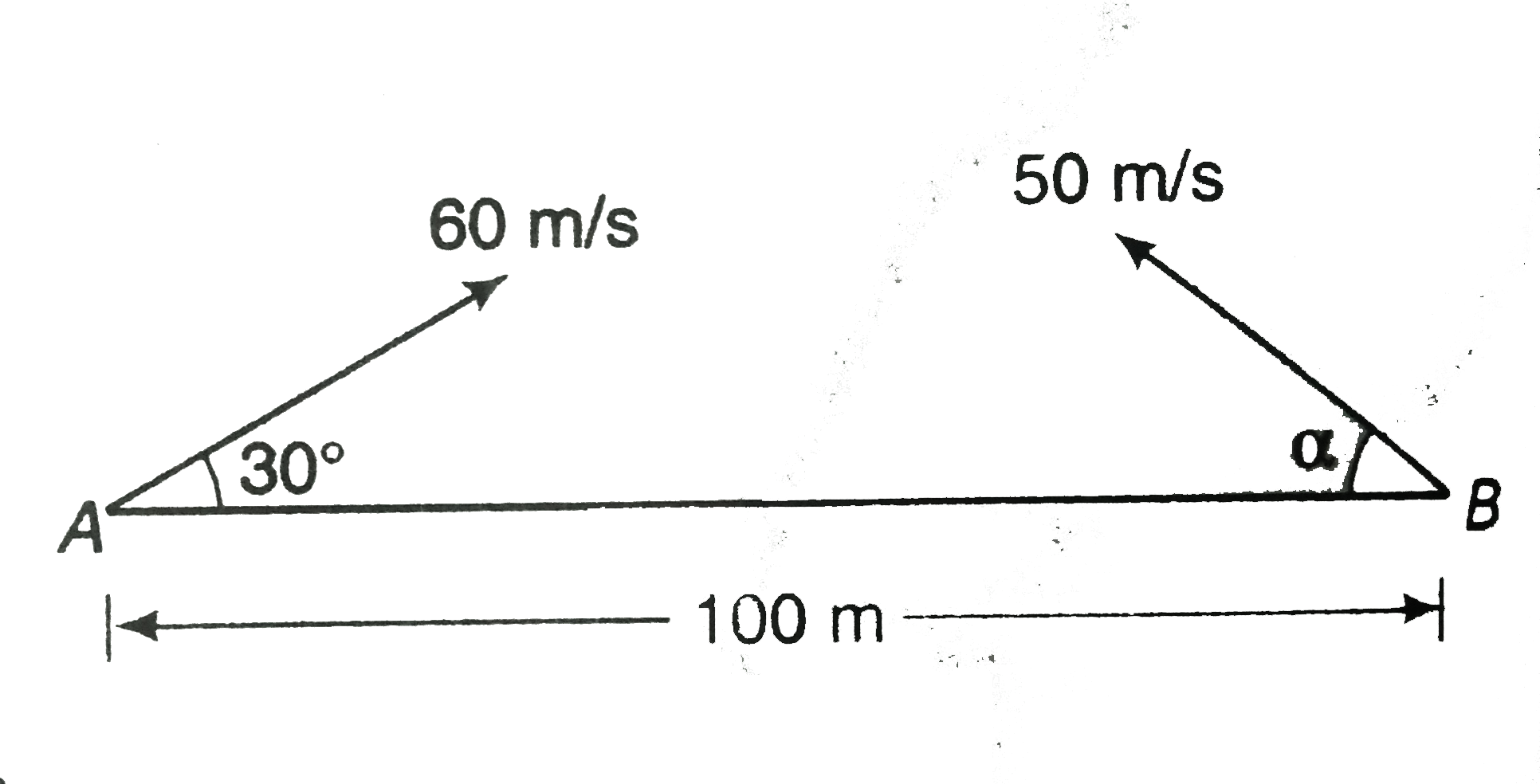
View SolutionA stone is projected from the ground with a velocity of 20 m/s at angle 30∘ with the horizontal. After one second it clears a wall then find height of the wall. (g=10ms−2)
View SolutionA particle A is projected from the ground with an initial velocity of 10m/s at an angle of 60∘ with horizontal. From what height should an another particle B be projected horizontally with velocity 5m/s so that both the particles collide in ground at point C if both are projected simultaneously g=10m/s2.
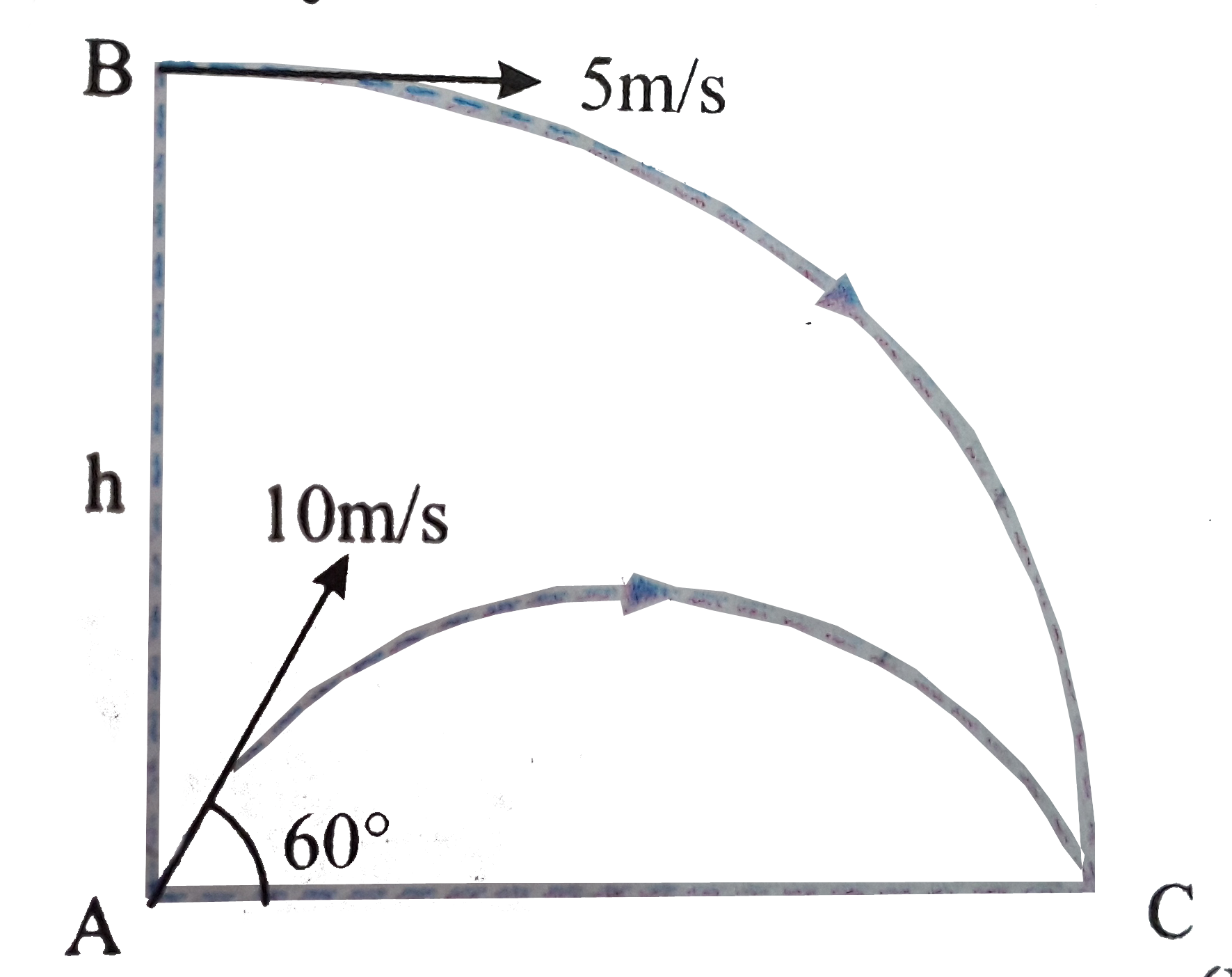
View SolutionA ball is thrown from the top of a tower with an initial velocity of 10m/s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
View Solution
