A particle (bob) of mass 1 kg is performing vertical cicular motion. Then :
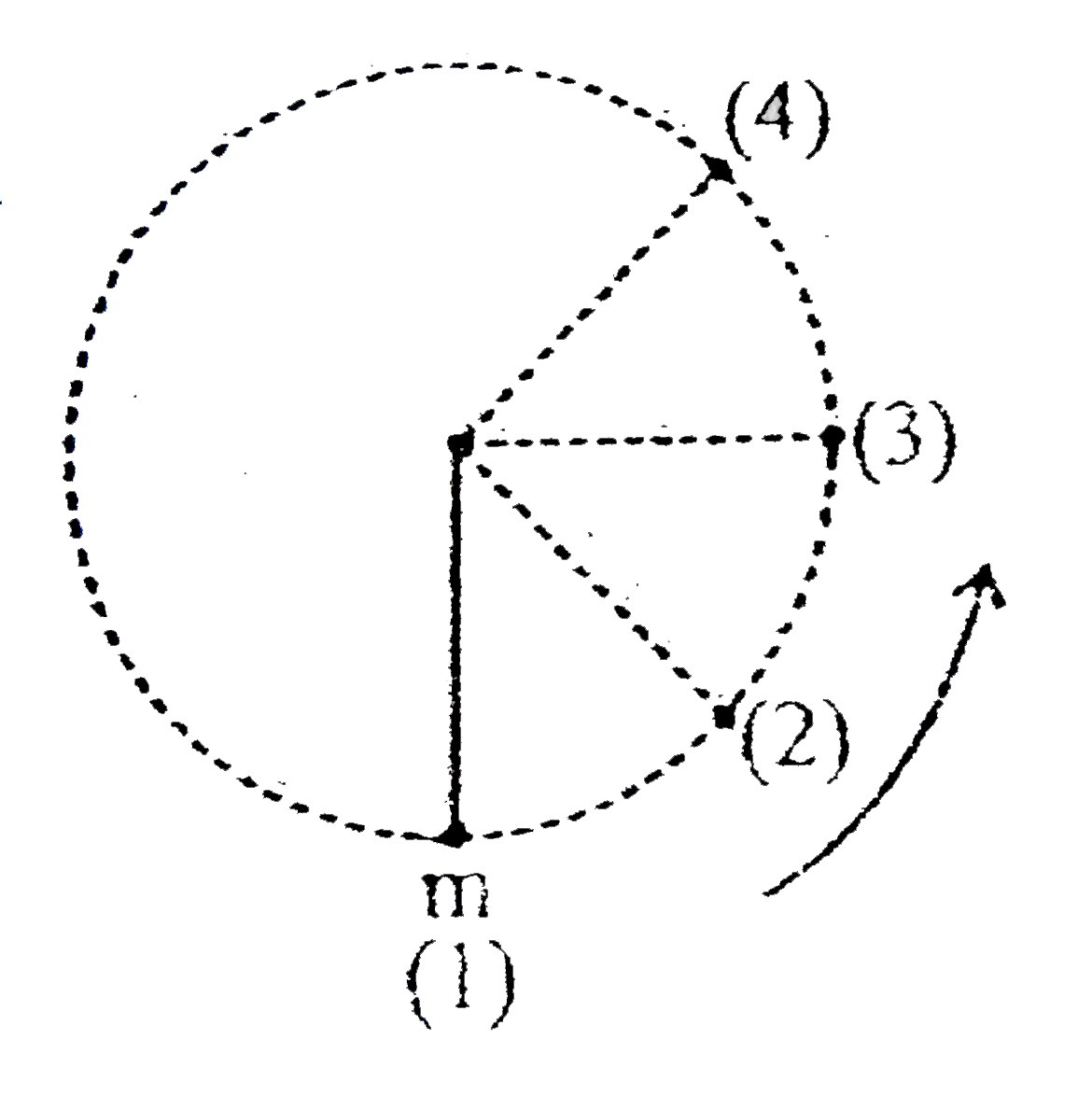
Power delevered by tension at point (4) is negative.
Power delevered by tension at point (2) is positive.
Power delivered by gravitational force at point (3) is zero.
Power delivered by gravitational force at point (4) is negative.
The correct Answer is:D
P=→F.→v Tension is always perpendicular to velocity
Topper's Solved these Questions
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
- TEST PAPER 1Book:ALLENChapter:TEST PAPER 1Exercise:PHYSICS
Explore 11 Videos
Similar Questions
A particle performing uniform circular motion has
View SolutionA mass is performing vertical ciruclar motion . If the average velocity of the particle is increased, then at which point the string will break:

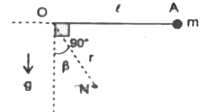
View SolutionA point mass m is connected with ideal inextensible string of length l and other end of string is tied at point O as shown in the figure. The string is made horizontal and mass is released from point A to perform vertical circular motion. There is a nail at point N such that ON =r . Find the value of r so that mass m is able to just perform complete vertical circular motion about point N.
View SolutionA horizontal platform with a small block of mass 1 kg kept on it performs vertical SHM of amplitude 1 cm. The block does not lose contact with the platform anywhere. The minimum possible time period of the platform
View SolutionA particle of mass 1031kg is moving with a velocity equal to 105ms−1. The wavelength of the particle is equal to
View SolutionFind the potential energy of 4-particles, each of mass 1 kg placed at the four vertices of a square of side length 1 m.
View SolutionA particle of mass 1kg is moving about a circle of radius 1m with a speed of 1m/s. Calculate the angular momentum of the particle.
View SolutionA particle of mass 1kg is moving about a circle of radius 1m with a speed of 1m/s. Calculate the angular momentum of the particle.
View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View Solution