An electric dipole of moment p is kept at a distance r form an infinite long charged wire of linear charge density λ as shown.Find the force acting on the dipole?

Field intensity at a distance r from the line of charge is E=λ2πε0r
The force on the dipole is F=−pdEdr
=−p[−2ε0r2]=p2ε0r2
Here the net force on dipole due to the wire will be attractive.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBook:NARAYNAChapter:ELECTRIC CHARGES AND FIELDSExercise:EVALUATE YOURSELF-1
Explore 10 Videos
- ELECTRIC CHARGES AND FIELDSBook:NARAYNAChapter:ELECTRIC CHARGES AND FIELDSExercise:EVALUATE YOURSELF-2
Explore 9 Videos
- DUAL NATUREBook:NARAYNAChapter:DUAL NATUREExercise:LEVEL-II (H.W)
Explore 17 Videos
- ELECTRO MAGNETIC INDUCTIONBook:NARAYNAChapter:ELECTRO MAGNETIC INDUCTIONExercise:Level-II (H.W)
Explore 23 Videos
Similar Questions
An electric dipole of moment p is kept at a distance r form an infinte long charged wire of linear charge density λ as shown.Find the force acting on the dipole?

View SolutionIn the figure shown, an electric dipole is placed at a distance x from an infinitely long rod of linear charge density λ.
(a) Find the net force acting on the dipole ?
(b) What is the work done in rotating the dipole through 180∘ ?
(c) If the dipole is slightly rotated about its equilibrium position, find the time period of oscillation. Assume that the dipole is linearly restrained.
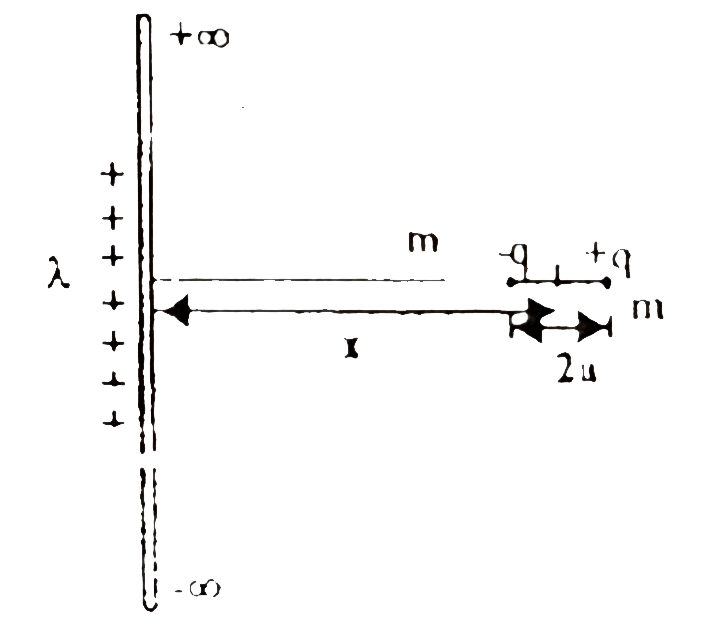
View Solution
Knowledge Check
If linear charge density of a wire as shown in the figure is λ
 Apotential at the centre is λ2ε0Belectric field at the centre of the loop is λ2πε0RCelectric field at the centre of the loop is λ2πε0R+λ2ε0RDNone of the above
Apotential at the centre is λ2ε0Belectric field at the centre of the loop is λ2πε0RCelectric field at the centre of the loop is λ2πε0R+λ2ε0RDNone of the aboveA tiny electric dipole of dipole moment p is palced at a distance r from an infinitely long wire, with its →p normal to the wire. If the linear charge density of the wire is λ, the electrostatic force acting on the dipole is equal to
AλP4πε0rBλPπε0rC2λPπε0rDλP2πε0r2A small electric dipole of dipole moment P is placed at a distance r from one infinitely long uniformly charged, straight conductor. If λ is the linear charge density of straight conductor and axis of the dipole is perpendicular to the straight conductor then the force acting on the dipole is
AλP2πε0r2BλP2πε0rCλP4πε0r2DλPπε0r2
In figure-, an electric dipole is placed at a distance x from an infinitely long rod of linear charge density λ.
(a) Find the net force acting on the dipole
(b) What is the work done in rotating the dipole through 180∘
(c ) If the dipole is slightly rotated about its equilibrium position, find the time period of oscillation. Assume that the dipole is linearly restrained.
[(a)λaqπ∈0x2,(b)2λaqπ∈0x,(c)2π√2π∈0mx2aλq]

View SolutionA dipole with an electric moment p is located at a distance r from a along thread charge uniformly with a linear density λ. Find the force F acting on the dipole if the vector p is oriented
(a) along the thread
(b) along the radius vector r
(c ) at the right angles to the thread and the radius vector r.
View SolutionA dipole of electric moment p is located at a distance r from a long thread charged with a linear density λ . Find the force on the dipole if (a) if is placed parallel to the thread , (b) perpendicular to the thread .
[Hint : Field due to long thread = 12πε0λr]
View SolutionAn electric dipole is placed at a distance x from centre O on the axis of a charged ring of R and charge Q uniformly distributed over it.
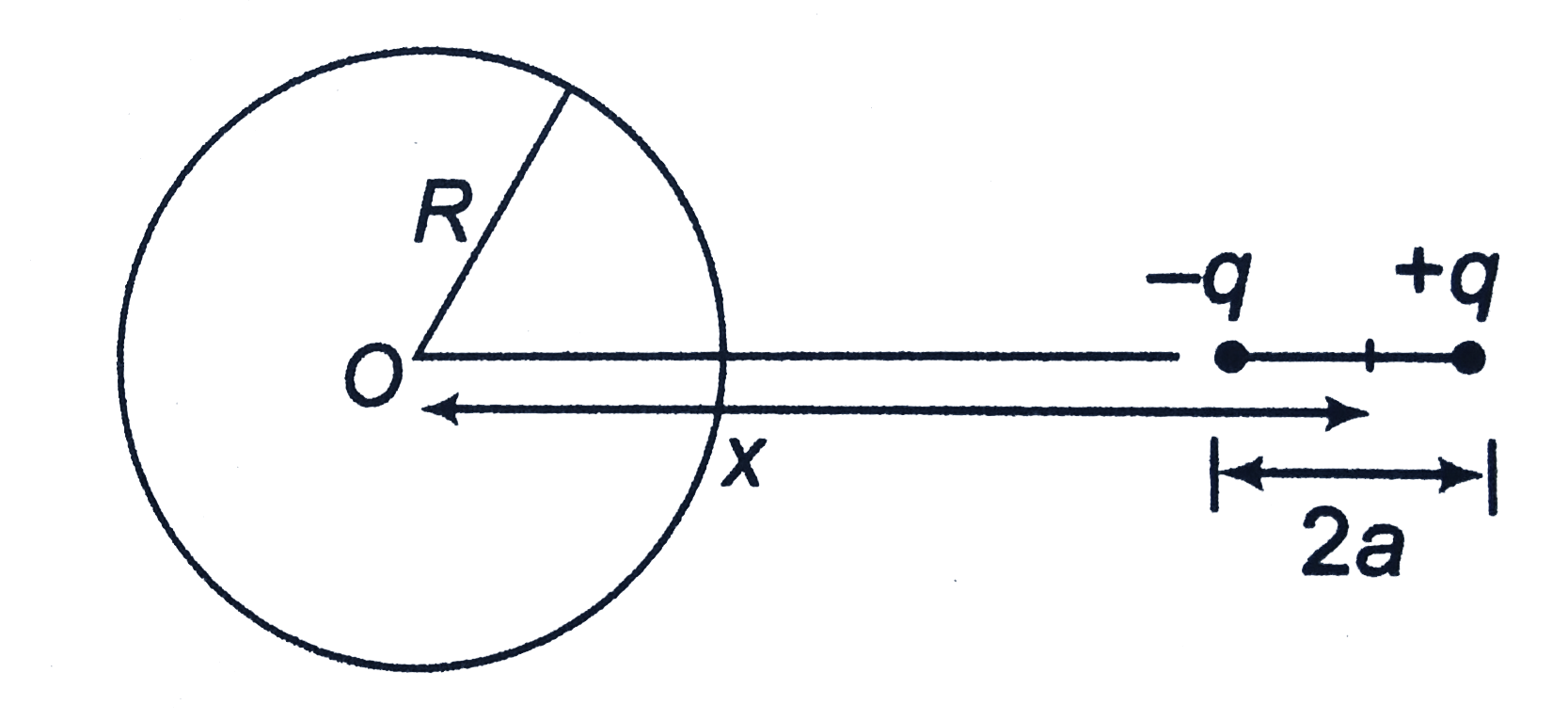
(a) Find the net force acting on the dipole.
(b) What is the work done in rotating the dipole through 180∘?
View SolutionA point charge q is placed at a distance r from a very long charged thread of unoform linear charge density λ. Find out total electric force experienced by the line charge due to the point charge. (Neglect gravity).
View Solution