Three identical conducting spheres A, B and C are given charges +Q, +q and -2Q respectively. A and C are brought in to contact and separated. Next B and C are brought in to contact and separated. If A,B and C are arranged so that their centres form an equilateral triangle and they do not touch each wihich of the following statement is correct regarding the forces between the pairs
(A,B),(B,C), and (C,A)?
(A,B) atrract, (B,C) attract, (C,A) repel
(A,B) attract, (B,C) repel, (C,A) repel
(A,B) atrract, (B,C) repel, (C,A) attract
(A,B) repel, (B,c) attract, (C,A) repel
The correct Answer is:C
To solve the problem step by step, we will analyze the charges on the spheres after they are brought into contact and then determine the forces between them.
Step 1: Initial Charges
- Sphere A has a charge of +Q.
- Sphere B has a charge of +q.
- Sphere C has a charge of −2Q.
Step 2: Contacting Spheres A and C
When spheres A and C are brought into contact, the total charge will be distributed equally between them because they are identical conducting spheres.
- Total charge when A and C are in contact:
QA+QC=+Q−2Q=−Q
- Each sphere will have half of this total charge after separation:
Q′A=Q′C=−Q2
Step 3: New Charges on A and C
After separation:
- Sphere A now has a charge of −Q2.
- Sphere C also has a charge of −Q2.
Step 4: Contacting Spheres B and C
Next, we bring sphere B (which has a charge of +q) into contact with sphere C (which now has a charge of −Q2).
- Total charge when B and C are in contact:
QB+Q′C=+q−Q2
- Each sphere will again have half of this total charge after separation:
Q′B=Q′′C=+q−Q22
Step 5: New Charges on B and C
After separation:
- Sphere B now has a charge of +q−Q22.
- Sphere C now has a charge of +q−Q22.
Step 6: Final Charges
- Sphere A: −Q2
- Sphere B: +q−Q22
- Sphere C: +q−Q22
Step 7: Analyzing Forces Between Spheres
Now, we need to analyze the forces between the pairs of spheres:
1. Force between A and B:
- A has a negative charge −Q2 and B has a positive charge +q−Q22.
- Since opposite charges attract, there will be an attractive force between A and B.
2. Force between B and C:
- Both B and C have the same charge +q−Q22.
- Since they are both positive, they will repel each other.
3. Force between C and A:
- C has a charge of +q−Q22 and A has a charge of −Q2.
- Again, since opposite charges attract, there will be an attractive force between C and A.
Conclusion
- The forces between the pairs are:
- A and B: Attractive
- B and C: Repulsive
- C and A: Attractive
Thus, the correct statement regarding the forces between the pairs (A, B), (B, C), and (C, A) is:
- A and B attract each other, B and C repel each other, and C and A attract each other.
- Sphere A has a charge of +Q.
- Sphere B has a charge of +q.
- Sphere C has a charge of −2Q.
When spheres A and C are brought into contact, the total charge will be distributed equally between them because they are identical conducting spheres.
QA+QC=+Q−2Q=−Q
- Each sphere will have half of this total charge after separation:
Q′A=Q′C=−Q2
After separation:
- Sphere A now has a charge of −Q2.
- Sphere C also has a charge of −Q2.
Next, we bring sphere B (which has a charge of +q) into contact with sphere C (which now has a charge of −Q2).
QB+Q′C=+q−Q2
- Each sphere will again have half of this total charge after separation:
Q′B=Q′′C=+q−Q22
After separation:
- Sphere B now has a charge of +q−Q22.
- Sphere C now has a charge of +q−Q22.
- Sphere A: −Q2
- Sphere B: +q−Q22
- Sphere C: +q−Q22
Now, we need to analyze the forces between the pairs of spheres:
1. Force between A and B:
- A has a negative charge −Q2 and B has a positive charge +q−Q22.
- Since opposite charges attract, there will be an attractive force between A and B.
- Both B and C have the same charge +q−Q22.
- Since they are both positive, they will repel each other.
- C has a charge of +q−Q22 and A has a charge of −Q2.
- Again, since opposite charges attract, there will be an attractive force between C and A.
- The forces between the pairs are:
- A and B: Attractive
- B and C: Repulsive
- C and A: Attractive
- A and B attract each other, B and C repel each other, and C and A attract each other.
Topper's Solved these Questions
Similar Questions
Two identical conducting balls A and B have charges- Q and + 3Q respectively. They are brought in contact with each other and then separated by a distance d part. Find the nature of the Coulomb force between them.
View SolutionTwo identical conducting balls A and B have charges -Q and +3Q respectively . They are brought in contact with each other and then separated by a distance d apart. Find the nature of the coulumb force between them.
View Solution
Knowledge Check
Two spheres are separately charged and then brought in contact, so
Atotal charge on the two spheres is conservedBtotal energy of the two spheres is conservedCBoth (a) and (b)Dnone of the aboveTwo spheres of equal mass A and B are given +q and -q charge respectively then
Amass of A increasesBmass of B increasesCmass of A remains constantDmass of B decreasesThree identical parallel conducting plates A, B and C are placed as shown. Switches S1andS2 are open, and can connect A and C to earth when closed. +Q charges is given to B.
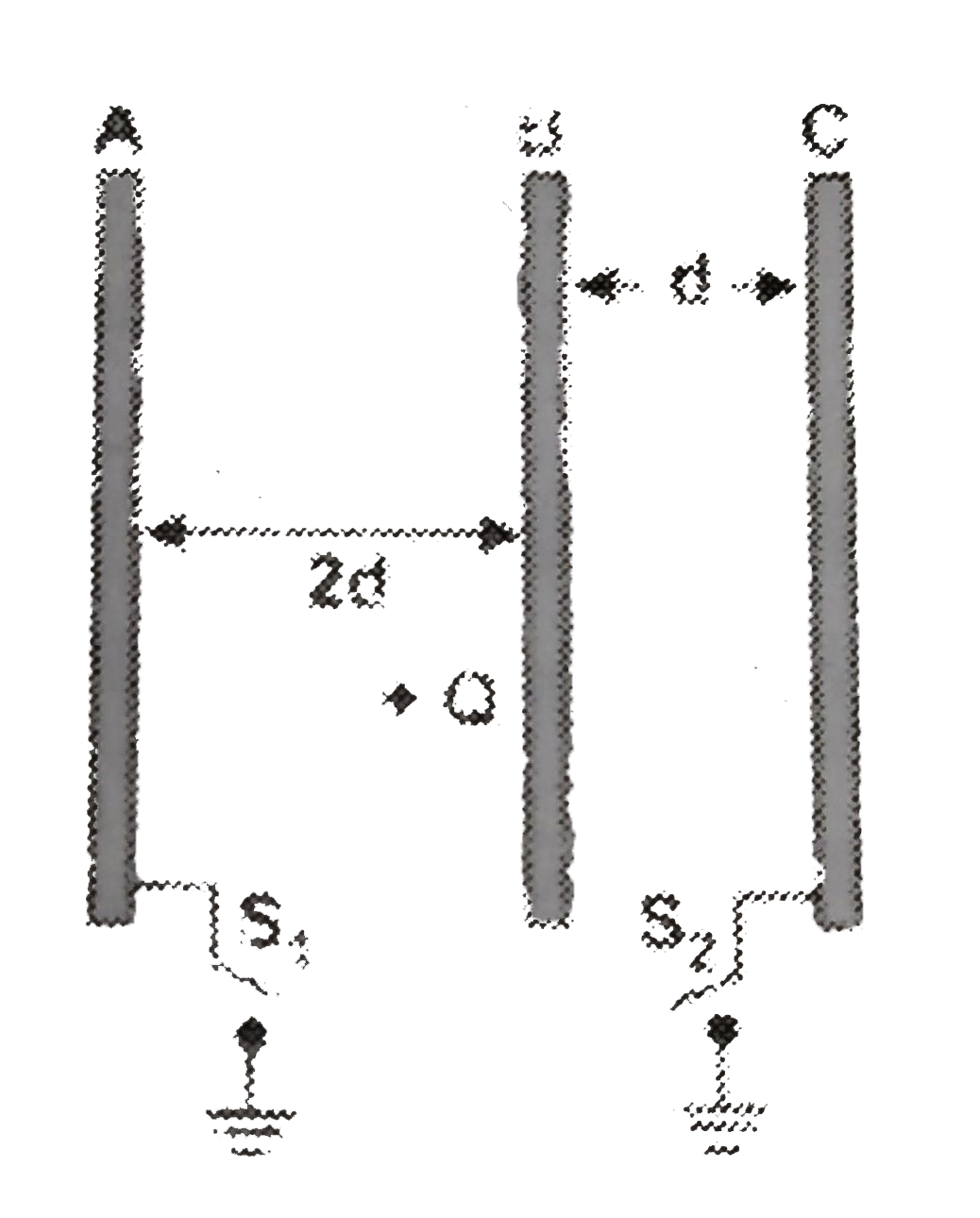 AIf S1is closed with S2 open, a charge of amount Q will pass through S1.BIf instead S2 were closed with S1 open, a charge of amount Q will pass through S2.CIf S1andS2 are closed together, a charge of amount 2Q/3 will pass through S2.DIf S1andS2 are closed together, a charge of amount 2Q/3 will pass through S1, and a charge of amount Q/3 will pass through S2.
AIf S1is closed with S2 open, a charge of amount Q will pass through S1.BIf instead S2 were closed with S1 open, a charge of amount Q will pass through S2.CIf S1andS2 are closed together, a charge of amount 2Q/3 will pass through S2.DIf S1andS2 are closed together, a charge of amount 2Q/3 will pass through S1, and a charge of amount Q/3 will pass through S2.
Consider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
View SolutionIf two conducting spheres are separately charged and then brought in contact
View SolutionIf two conducting spheres are separately charged and then brought in contact
View SolutionIf two conducting spheres are separately charged and then brought in contact.
View SolutionTwo identical metal spheres posses +60C and −20C of charges .They are brought in contact and then separated by 10cm .the force between them is
View Solution
