A uniform electrif field of intensit E is in the Y-negative direction. An electron of mass m and charge e is fired through the origin with initial velocity u in the X-positive direction. The displacement undergone of the electron during a time interval t is
ut
2Et2/2m
√ut+(eEt2/2m)2
√ut−(eEt2/2m)2
The correct Answer is:B
To solve the problem, we need to analyze the motion of the electron under the influence of the electric field. The electric field is directed in the negative y-direction, and the electron is fired with an initial velocity in the positive x-direction. We will calculate the displacement of the electron in both the x and y directions and then find the total displacement.
1. Identify the Forces Acting on the Electron:
- The electron has a charge e and is subjected to an electric field E in the negative y-direction.
- The force F on the electron due to the electric field is given by:
F=eE
- This force causes an acceleration ay in the y-direction, calculated using Newton's second law:
F=ma⟹ay=Fm=eEm
2. Analyze Motion in the X-Direction:
- The initial velocity in the x-direction is u.
- Since there is no force acting in the x-direction, the acceleration ax=0.
- The displacement in the x-direction Sx after time t is given by:
Sx=ut+12axt2=ut+12⋅0⋅t2=ut
3. Analyze Motion in the Y-Direction:
- The initial velocity in the y-direction uy=0 (since it is fired horizontally).
- The displacement in the y-direction Sy after time t is given by:
Sy=uyt+12ayt2=0+12(eEm)t2=eE2mt2
4. Calculate the Total Displacement:
- The total displacement S of the electron can be found using the Pythagorean theorem since the displacements in the x and y directions are perpendicular:
S=√S2x+S2y=√(ut)2+(eE2mt2)2
- Substituting the expressions for Sx and Sy:
S=√(ut)2+(eE2mt2)2
Final Answer:
The displacement undergone by the electron during the time interval t is:
S=√(ut)2+(eE2mt2)2
- The electron has a charge e and is subjected to an electric field E in the negative y-direction.
- The force F on the electron due to the electric field is given by:
F=eE
- This force causes an acceleration ay in the y-direction, calculated using Newton's second law:
F=ma⟹ay=Fm=eEm
- The initial velocity in the x-direction is u.
- Since there is no force acting in the x-direction, the acceleration ax=0.
- The displacement in the x-direction Sx after time t is given by:
Sx=ut+12axt2=ut+12⋅0⋅t2=ut
- The initial velocity in the y-direction uy=0 (since it is fired horizontally).
- The displacement in the y-direction Sy after time t is given by:
Sy=uyt+12ayt2=0+12(eEm)t2=eE2mt2
- The total displacement S of the electron can be found using the Pythagorean theorem since the displacements in the x and y directions are perpendicular:
S=√S2x+S2y=√(ut)2+(eE2mt2)2
- Substituting the expressions for Sx and Sy:
S=√(ut)2+(eE2mt2)2
The displacement undergone by the electron during the time interval t is:
S=√(ut)2+(eE2mt2)2
Topper's Solved these Questions
Similar Questions
An electron of mass ‘M’ kg and charge ‘e’ coulomb travels from rest through a potential difference of ‘V’ volt. The final velocity of the electron is (in m/s)
View SolutionLet there be a uniform electric field "E" existing along the positive X-direction.Assume electric potential to be zero at the origin.Potential at the point x=x0 is
View Solution
Knowledge Check
In a region of space, a uniform magnetic field B exists in the x-direction. An electron is fired from the origin with its initial velocity u making an angle α with the y direction in the y-z plane. In the subsequent motion of the electron,
 Ay-coordinate of the electron will never be negativeBz-coordinate of the electron will never be negativeCx-coordinate of the electron will never be negativeDtrajectory of the electron would be helical
Ay-coordinate of the electron will never be negativeBz-coordinate of the electron will never be negativeCx-coordinate of the electron will never be negativeDtrajectory of the electron would be helicalA ball of mass 'm' is thrown at an angle is 'θ' with the horizontal with an initial velocity 'u'.The change in its momentum during its flight in a time interval of 't' is
AmgtBm>cosθCm>sinθD1/2m>.An electron of mass m and charge e is accelerated from rest through a potential difference V in vacuum. The final speed of the electron will be
AV√e/mB√eV/mC√2eV/mD2eV/m
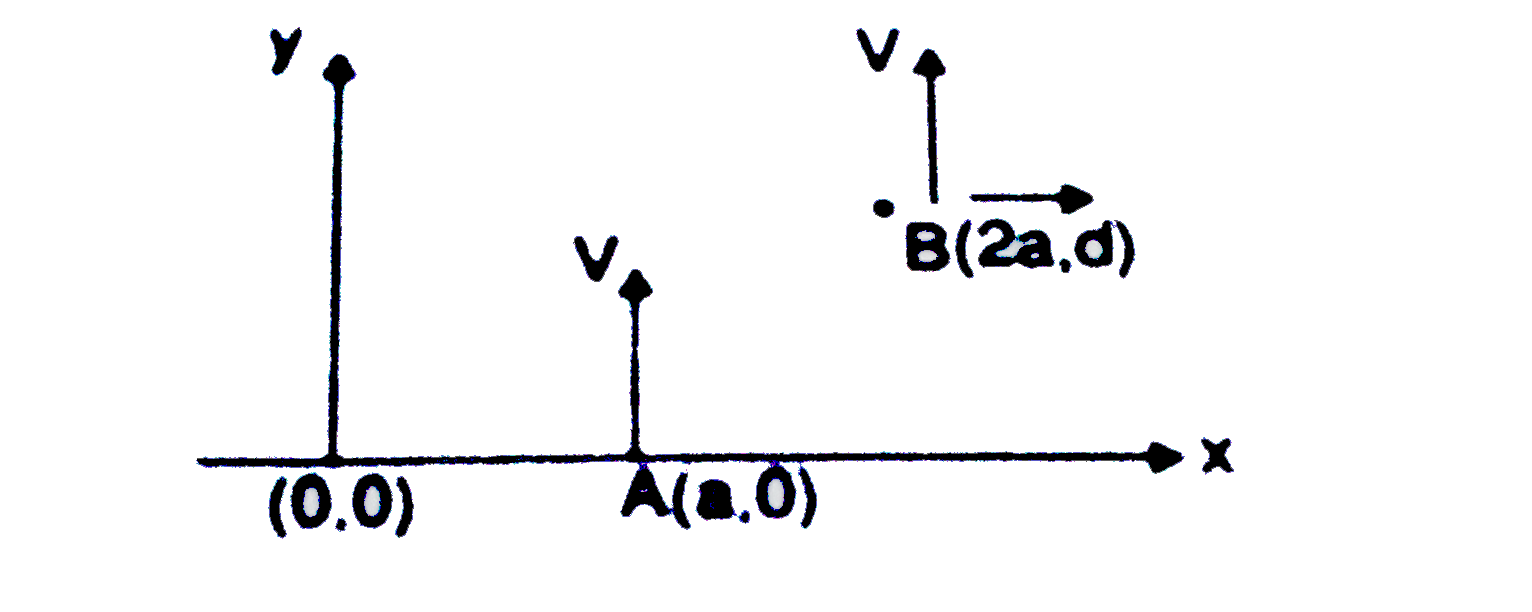
A uniform electric field of strength e exists in a region. An electron (charge -e, mass m) enters a point A with velocity Vˆj. It moves through the electric field & exits at point B. Then :
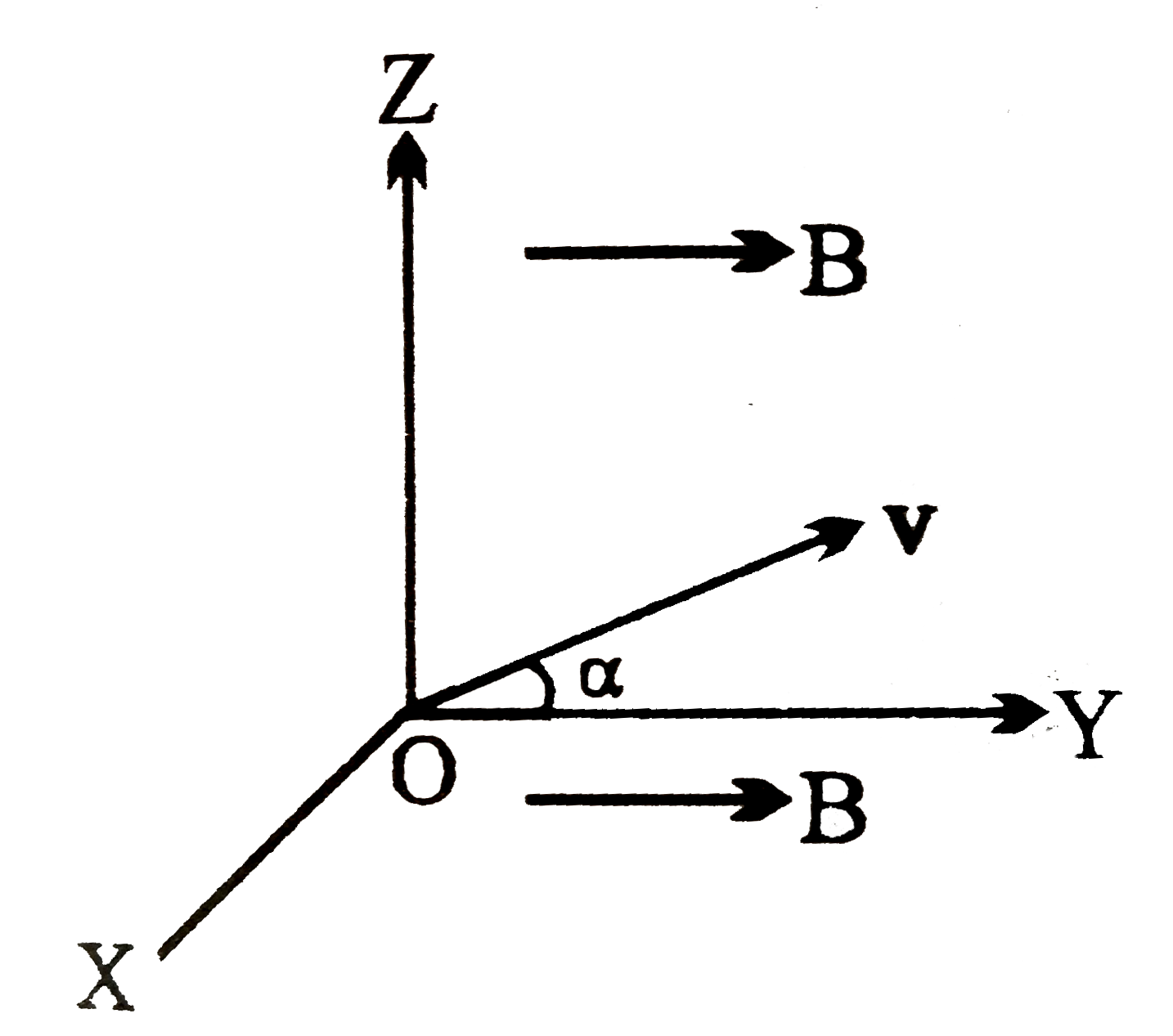
View SolutionIn a region of space, a uniform magnetic field B exists in the y-direction A proton is fired from the origin, with its initial velocity v making a small angle alpha with the y-direction in the yz plane. In the subsequent motion of the proton
 .
.
View SolutionWhen an electron fo mass 6 m and charge 6e moves with a velocity of 7u about the nuclar charge Ze in a circular orbit fo radius r . The potential energy of the electron will be:
View SolutionAn electron moving with a uniform velocity along the positive x-direction enters a magnetic field directed along the positive y-direction. The force on the electron is directed along
View SolutionAn uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V. It moves through the electric field and exists at point B. The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged.
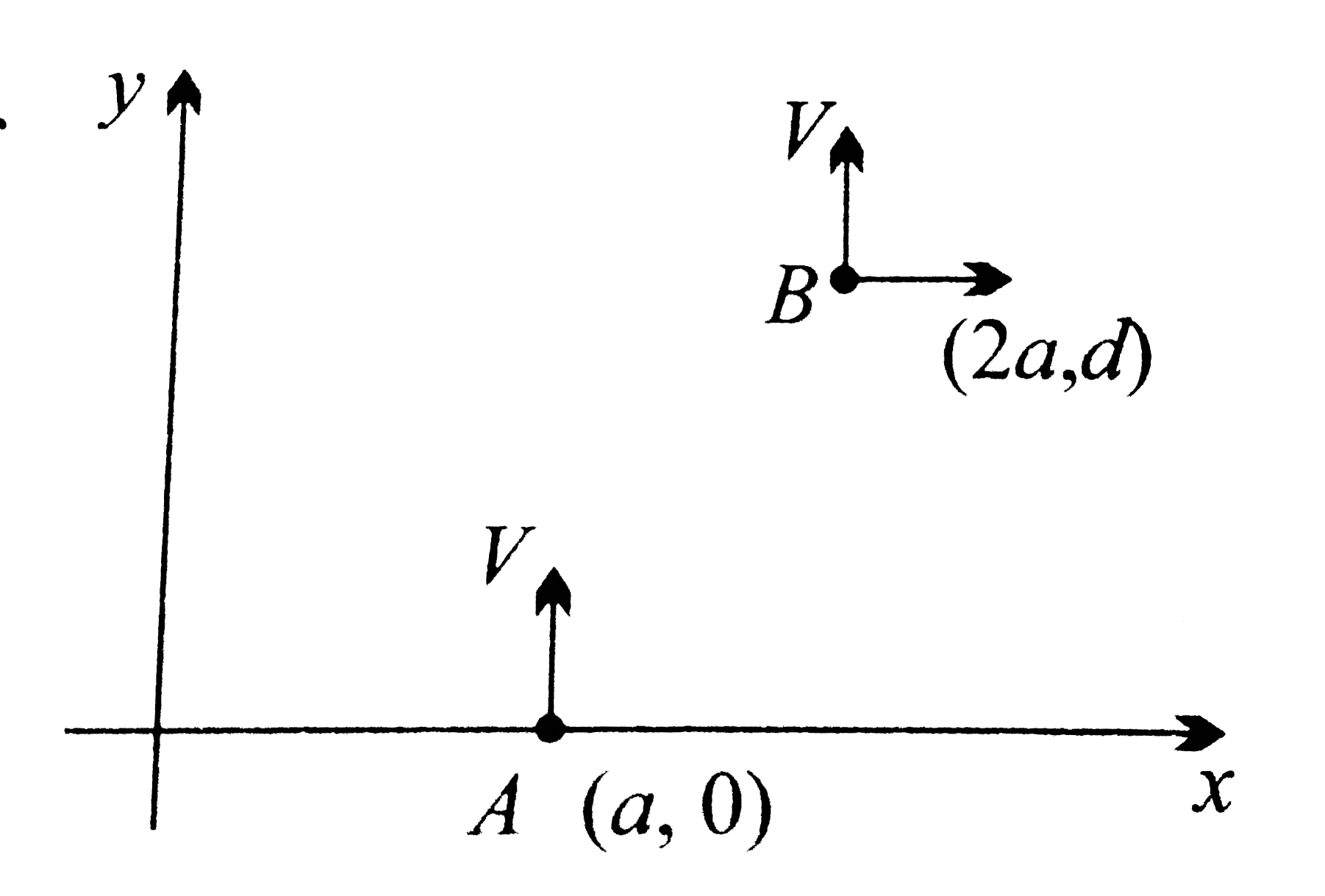 .
.
Find electric field.
View Solution
