A positive charge kept at one of the vertices of a regular hexagon produces electric intensity E at the centre of the hexagon. If the charge is moved to an adjacent vertex, the magnitude of change in the electric intensity will be
zero
√3E
E
E/√3
The correct Answer is:c
To solve the problem, we need to analyze the electric field produced by a positive charge at the vertices of a regular hexagon and how it changes when the charge is moved to an adjacent vertex. Here's a step-by-step solution:
Step 1: Understanding the Setup
We have a regular hexagon with a positive charge +q placed at one of its vertices. This charge produces an electric field E at the center of the hexagon.
Hint: Visualize the hexagon and label the vertices and the center clearly.
Step 2: Electric Field at the Center
The electric field E at the center of the hexagon due to the charge at vertex A (let's say) can be expressed as:
E1=kqa2
where k is Coulomb's constant and a is the distance from the charge to the center of the hexagon.
Hint: Remember that the electric field due to a point charge is inversely proportional to the square of the distance.
Step 3: Moving the Charge to an Adjacent Vertex
When the charge is moved to an adjacent vertex (let's say from A to B), it will produce a new electric field E2 at the center of the hexagon:
E2=kqa2
The magnitudes of E1 and E2 are the same since the distance from the charge to the center remains unchanged.
Hint: The magnitudes of the electric fields due to the charge at both vertices are equal.
Step 4: Analyzing the Direction of the Electric Fields
The direction of the electric field E1 due to the charge at vertex A will point towards the center, while the electric field E2 due to the charge at vertex B will also point towards the center but at an angle of 60∘ from E1 because of the geometry of the hexagon.
Hint: Use symmetry and geometry to determine the angles between the electric field vectors.
Step 5: Calculating the Change in Electric Field
To find the change in electric field when the charge is moved, we can use the vector addition of the electric fields:
ΔE=|E2−E1|
Using the cosine rule for the angle between the two vectors:
|ΔE|=√E21+E22−2E1E2cos(60∘)
Since E1=E2=E:
|ΔE|=√E2+E2−2E2⋅12=√2E2−E2=√E2=E
Hint: Remember that cos(60∘)=12.
Step 6: Conclusion
Thus, the magnitude of the change in electric intensity when the charge is moved to an adjacent vertex is:
ΔE=E
Final Answer: The change in electric intensity is E.
We have a regular hexagon with a positive charge +q placed at one of its vertices. This charge produces an electric field E at the center of the hexagon.
The electric field E at the center of the hexagon due to the charge at vertex A (let's say) can be expressed as:
E1=kqa2
where k is Coulomb's constant and a is the distance from the charge to the center of the hexagon.
When the charge is moved to an adjacent vertex (let's say from A to B), it will produce a new electric field E2 at the center of the hexagon:
E2=kqa2
The magnitudes of E1 and E2 are the same since the distance from the charge to the center remains unchanged.
The direction of the electric field E1 due to the charge at vertex A will point towards the center, while the electric field E2 due to the charge at vertex B will also point towards the center but at an angle of 60∘ from E1 because of the geometry of the hexagon.
To find the change in electric field when the charge is moved, we can use the vector addition of the electric fields:
ΔE=|E2−E1|
Using the cosine rule for the angle between the two vectors:
|ΔE|=√E21+E22−2E1E2cos(60∘)
Since E1=E2=E:
|ΔE|=√E2+E2−2E2⋅12=√2E2−E2=√E2=E
Thus, the magnitude of the change in electric intensity when the charge is moved to an adjacent vertex is:
ΔE=E
Topper's Solved these Questions
Similar Questions
Six equal point charges are placed at the corners of a regular hexagon of side 'a'. Calculate electric field intensity at the centre of hexagon ?
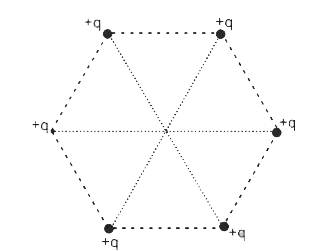
View SolutionFive identical charges are kept at five vertices of a regular hexagon. Match the following two columns at centre of the hexagon. If in the given situation electric field at centre is E, then,

View Solution
Knowledge Check
Electric intensity at a place due to a charge is
Avector quantityBscalar quantityCunitless quantityDdimensionless quantitySix negative equal charge are placed at the vertical of a regular hexagon . 6q charge is placed at the centre of the hexagon . Find the electric dipole moment of the system.
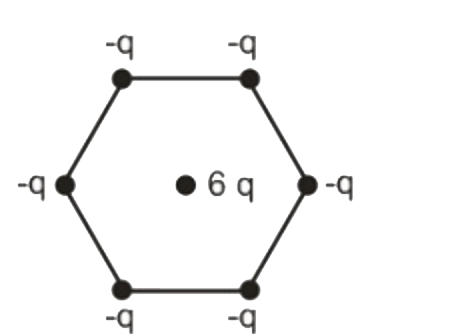 AzeroB6qaC3qaDqa
AzeroB6qaC3qaDqaElectric intensity at a point near a charged sphere of charge q is given by
AE=14π∈0K⋅qr2BE=12π∈0K⋅qrCE=σ∈0kDnone of these
Four identical point charges, each of charge q, are placed on the vertices of a regular hexagon of side a such that the net electric field at centre of hexagon is zero. If one of the charge is now removed, then the electric field at centre of hexagon is k- 4.60
View SolutionThe point charges are placed on the vertices of regular hexagon of side L as shown. Find the potential energy of the system of charges.
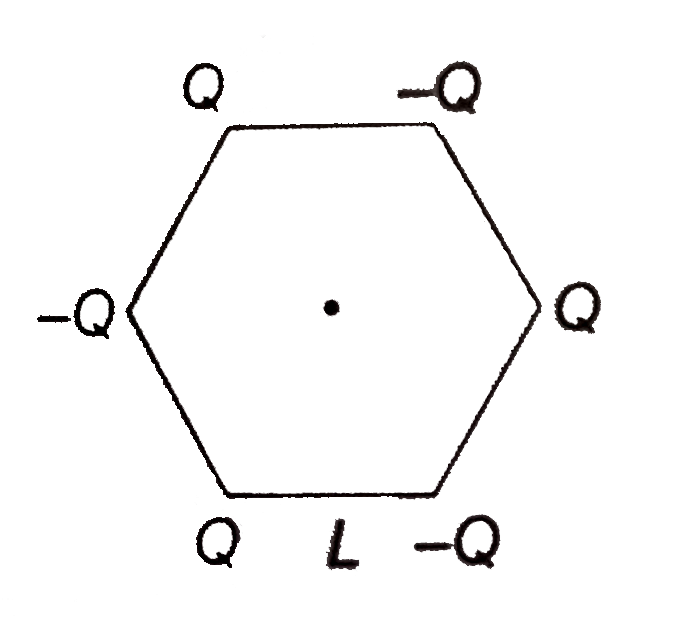
View SolutionFive point charges, each +q are placed on five vertices of a regular hexagon of side' l '. Find the magnitude of the resultant force on a charge –q placed at the centre of the hexagon.
View SolutionTwo charges e and 3e are placed at a distance r. The distance of the point where the electric field intensity will be zero is
View SolutionThe electric field intensity on the surface of a charged conductor is
View Solution
