Point P is at a distance of r(>R) from the axis of the cylinder. The volume charge densilty and radius of this cylinder are n and r respectively

What is the electric field at point P?
ρR22ε0r
ρR22ε0
ρR2ε0r
ρR2ε0
The correct Answer is:A
∮→E.d→A=qε0
let l be the length of the cylinder.
Total charge on the cylinder q=r(pR2l)
⇒E(2πrl)=ρπR2lε0
⇒E=ρR22ε0r
Topper's Solved these Questions
Similar Questions
An infinitely long cylindrical shell ofinner radius r1 and outer radius r2 is charged in its volume with a volume charge density which varies with distance from axis of cylinder as p=blrC/m3 which C is a positive constant and r is the distance from axis of cylinder. Find the electric field intensity at a point P at a distance x from axis of cylinder
View SolutionIn a long insulating cylinder of radius R a cylindrical tunnel of radius a located at a distance b from the axis of the cylinder as shown in the figure. R R b - The solid part of the cylinder has a uniform volume charge density P. Find the magnitude and direction of the electric field inside the tunnel.
View Solution
Knowledge Check
A cylindrical region of radius R contains a uniform magnetic field parallel to axis with magnitude that is changing linearly with time. If r is the radial distance of a point from axis of cylinder in a plane perpendicular to axis then the magnitude of the induced electrical field outside the cylinder is directly proportional to
ArBr2C1/rD1/r2
A cylindrical portion of radius r is removed from a solid sphere of radius R and uniform volume charge density ρ in such a way that the axis of the hollow cylinder coincides with one of the diameters of the sphere. (r is negligible compared to R). Then the electric field intensity at point A isAρr3ε0ˆiB−ρr3ε0ˆiCρr6ε0ˆiD−ρr6ε0ˆiPositive and negative charges of equal magnitude lie along the symmetry axis of a cylinder. The distance from the positive charge to the left - end cap of the cylinder is the same as the distance from the negative charge to the right - end cap.

What is the flux of the electric field through the closed cylinder ?AzeroB+Q/ε0C+2Q/ε0D−Q/ε0
A dielectric cylinder of radius a is infinitely long. It is non-uniformly charged such that volume charge density ρ varies directly as the distance from the cylinder. Calculate the electric field intensity due to it at a point located at a distance r from the axis of the cylinder. Given that ρ is zero at the axis and it is equal to ρ on the surface of cylinder. Also calculate the potential difference between the axis and the surface. [ρr23∈0a,ρa29∈0]
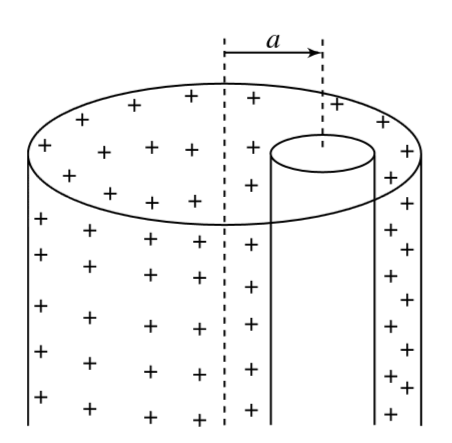
View Solution(a) There is a long uniformly charged cylinder having a volume charge density of ρC/m3. Radius of the cylinder is R. Find the electric field at a point at a distance x from the axis of the cylinder for following cases (i) x lt R (ii) x gt R What is the maximum field produced by the charge distribution at any point? (b) The cylinder described in (a) has a long cylindrical cavity. The axis of cylindrical cavity is at a distance a from the axis of the charged cylinder (see figure). Find electric field inside the cavity.
View SolutionWhat is the volume of a hollow cylinder with R, r and h as outer radius, inner radius and height respectively?
View SolutionA small point mass m is to be thrown with such a speed at a distance x from the axis of a long cylinder of radius R and density ρ, so that m starts revolving around the cylinder in a circular orbit of radius x with centre on the axis of cylinder. Find the speed with which point mass is thrown.
View SolutionA cylindrical space of radius R is filled with a uniform magnetic induction parallel to the axis of the cylinder. If B charges at a constant rate, the graph showin the variation of induced electric field with distance r from the axis of cylinder is
View Solution
