An equilaterial triangle ABC has a side a. Two infinitely long thin straight wires having uniform linear charge densities ' lamda ' and '-lamda' are arranged at A and B perpendicular to the plante of the triangle. The magnitude of electric intensity at the third vertex c will be
λ2πε0a
λπε0a
zero
√3λ2πε0a
The correct Answer is:A
To find the magnitude of the electric intensity at vertex C of the equilateral triangle ABC, we will follow these steps:
Step 1: Understand the Setup
We have an equilateral triangle ABC with side length 'a'. There are two infinitely long straight wires with uniform linear charge densities λ at point A and −λ at point B, both perpendicular to the plane of the triangle.
Step 2: Electric Field Due to Each Wire
The electric field E due to an infinitely long wire with linear charge density λ at a distance r is given by the formula:
E=λ2πϵ0r
where ϵ0 is the permittivity of free space.
Step 3: Calculate the Distance from A and B to C
In our equilateral triangle:
- The distance from A to C and from B to C is equal to the side length a.
Step 4: Calculate Electric Fields at C
1. Electric Field due to wire at A (positive charge):
- The electric field EA at point C due to the wire at A is directed radially outward from A.
- The magnitude is:
EA=λ2πϵ0a
2. Electric Field due to wire at B (negative charge):
- The electric field EB at point C due to the wire at B is directed radially inward towards B.
- The magnitude is:
EB=λ2πϵ0a
Step 5: Analyze the Directions
Since the triangle is equilateral, the angles at vertices A and B are 60∘. The electric fields EA and EB will have components in the horizontal direction (along line AC and BC) and vertical direction (perpendicular to line AB).
Step 6: Resolve Electric Fields into Components
1. Horizontal Components:
- The horizontal component of EA at C:
EA,x=EAcos(60∘)=λ2πϵ0a⋅12=λ4πϵ0a
- The horizontal component of EB at C:
EB,x=EBcos(60∘)=λ2πϵ0a⋅12=λ4πϵ0a
2. Vertical Components:
- The vertical components will cancel each other out since EA is directed outward and EB is directed inward.
Step 7: Calculate the Net Electric Field at C
The net electric field Enet at point C is the sum of the horizontal components:
Enet=EA,x+EB,x=λ4πϵ0a+λ4πϵ0a=λ2πϵ0a
Final Answer
Thus, the magnitude of the electric intensity at vertex C is:
Enet=λ2πϵ0a
---
We have an equilateral triangle ABC with side length 'a'. There are two infinitely long straight wires with uniform linear charge densities λ at point A and −λ at point B, both perpendicular to the plane of the triangle.
The electric field E due to an infinitely long wire with linear charge density λ at a distance r is given by the formula:
E=λ2πϵ0r
where ϵ0 is the permittivity of free space.
In our equilateral triangle:
- The distance from A to C and from B to C is equal to the side length a.
1. Electric Field due to wire at A (positive charge):
- The electric field EA at point C due to the wire at A is directed radially outward from A.
- The magnitude is:
EA=λ2πϵ0a
- The electric field EB at point C due to the wire at B is directed radially inward towards B.
- The magnitude is:
EB=λ2πϵ0a
Since the triangle is equilateral, the angles at vertices A and B are 60∘. The electric fields EA and EB will have components in the horizontal direction (along line AC and BC) and vertical direction (perpendicular to line AB).
1. Horizontal Components:
- The horizontal component of EA at C:
EA,x=EAcos(60∘)=λ2πϵ0a⋅12=λ4πϵ0a
- The horizontal component of EB at C:
EB,x=EBcos(60∘)=λ2πϵ0a⋅12=λ4πϵ0a
- The vertical components will cancel each other out since EA is directed outward and EB is directed inward.
The net electric field Enet at point C is the sum of the horizontal components:
Enet=EA,x+EB,x=λ4πϵ0a+λ4πϵ0a=λ2πϵ0a
Thus, the magnitude of the electric intensity at vertex C is:
Enet=λ2πϵ0a
Topper's Solved these Questions
Similar Questions
Two long wires having linear charge density λ and −λ are placed parallel to each other at separation ras shown in the figure. The electric field at point P will be
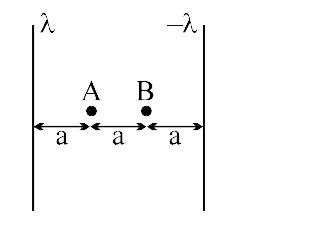
View SolutionBetween two infinitely long wires having linear charge densities λ and −λ there are two points A and B shown in the figure. The amount of work done by the electric field moving a point charge q0 from A to B is equal to
View Solution
Knowledge Check
Two infinitely long thin styraight wires having uniform linear charge densities λ and 2λ are arranged parallel to each other at a distance r apart.The intensity of the electric field at a point midway between them is
A2λπε0Bλπε0rCλ2πε0rD3λ2πε0rThe electric field intensity due to a thin infinity long straight wire of uniform linear charge density λ at O is-
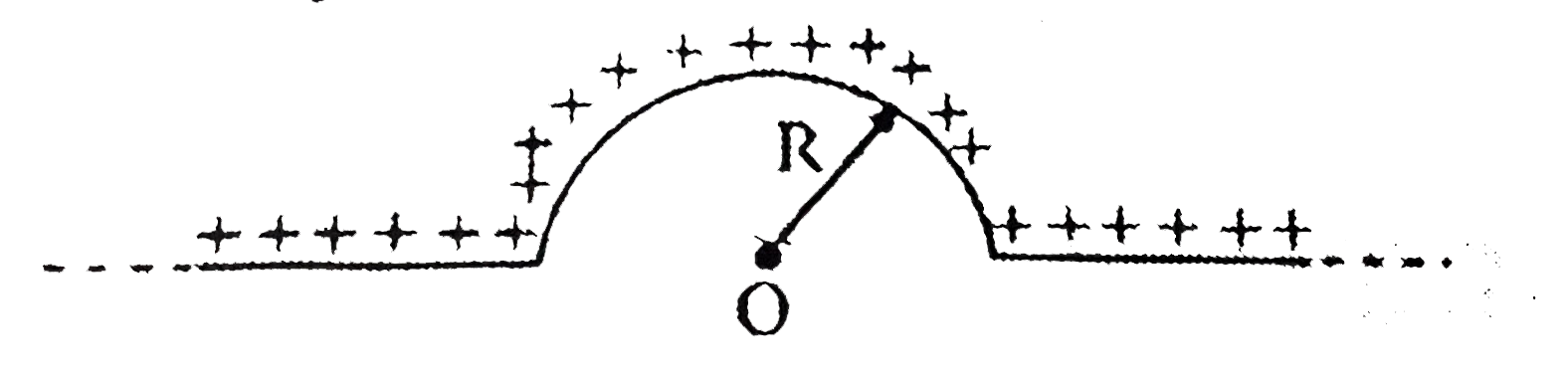 Aλ2πε0RBλ√22πε0RCλ√52πε0RDzero
Aλ2πε0RBλ√22πε0RCλ√52πε0RDzeroAn infinitely long thin straight wire has uniform linear charge density of 1/3coulm−1 .Then the magnitude of the electric intensity at a point 18cm away is
A0.33×1011N/CB3×1011NC−1C0.66×1011NC−1D1.32×1011NC−1
Two charge +Q each are placed at the two verticles of an equilateral triangle of side a .The intensity of electric field at the third vertex is
View SolutionWrite the expression of electric field due to an infinitely long, straight, wire having linear charge density λ at a point that is at a distance r from it.
View SolutionBetween two infinitely long wires having linear charge densities λ and −λ , there are two points A and B as shown in the figure. The amount of work done by the electric field in moving a point charge q0 from A to B is equal to :

View SolutionFigure shows an equilateral triangle ABC of side l carrying currents as shown, and placed in a uniform magnetic field B perpendicular to the plane of triangle. The magnitude of magnetic force on the triangle is

View SolutionEqual charges q are placed at the vertices A and B of an equilatral triangle ABC of side a. The magnitude of electric field at the point C is
View Solution