Two point charges are fixed on the Xaxis , q1=12.0mC is located at the origin and q2=−3.0mC is located at point A, with x2=8.0cm. Where should a third charge q3, be placed on the X-axis so that the total, electrostatic force acting on it is zero?
at x3=16cm
at x3=12cm
at x3=24cm
at x3=6cm
The correct Answer is:C
To solve the problem of where to place the third charge q3 so that the total electrostatic force acting on it is zero, we can follow these steps:
Step 1: Understand the Configuration
We have two charges:
- q1=12.0mC (positive) located at the origin (0,0).
- q2=−3.0mC (negative) located at (8.0cm,0).
We need to find the position of a third charge q3 on the x-axis such that the net electrostatic force acting on it is zero.
Step 2: Analyze Possible Positions for q3
The third charge q3 can be placed in three possible regions:
1. To the left of q1 (i.e., x<0)
2. Between q1 and q2 (i.e., 0<x<8)
3. To the right of q2 (i.e., x>8)
Step 3: Evaluate Each Region
1. Left of q1:
- If q3 is positive, it will be repelled by q1 and attracted by q2. The forces will act in opposite directions, potentially balancing each other.
2. Between q1 and q2:
- If q3 is positive, it will be repelled by q1 and attracted by q2. The net force cannot be zero since both forces will act in the same direction.
3. Right of q2:
- If q3 is positive, it will be repelled by q2 and attracted by q1. The forces will act in opposite directions, potentially balancing each other.
Step 4: Set Up the Equation for Forces
Assuming q3 is placed at a distance x from the origin (to the left of q1), the distances to the charges are:
- Distance from q1: |x|
- Distance from q2: 8+|x|
Using Coulomb's Law, we can express the forces:
- Force due to q1 on q3:
F1=k|q1⋅q3|x2
- Force due to q2 on q3:
F2=k|q2⋅q3|(8+|x|)2
Setting the magnitudes of the forces equal for equilibrium:
k12⋅q3x2=k3⋅q3(8+|x|)2
Step 5: Simplify the Equation
Since k and q3 are common on both sides, they can be canceled out:
12x2=3(8+|x|)2
Cross-multiplying gives:
12(8+|x|)2=3x2
Step 6: Expand and Rearrange
Expanding the left side:
12(64+16|x|+x2)=3x2
768+192|x|+12x2=3x2
Rearranging gives:
9x2+192|x|+768=0
Step 7: Solve the Quadratic Equation
Using the quadratic formula:
x=−b±√b2−4ac2a
where a=9,b=192,c=768:
x=−192±√1922−4⋅9⋅7682⋅9
Calculating the discriminant:
1922=36864
4⋅9⋅768=27648
√36864−27648=√9216=96
Now substituting back:
x=−192±9618
Calculating the two possible values:
1. x=−9618=−5.33cm
2. x=−28818=−16cm
Conclusion
The valid position for q3 is x=−16cm (to the left of the origin).
We have two charges:
- q1=12.0mC (positive) located at the origin (0,0).
- q2=−3.0mC (negative) located at (8.0cm,0).
The third charge q3 can be placed in three possible regions:
1. To the left of q1 (i.e., x<0)
2. Between q1 and q2 (i.e., 0<x<8)
3. To the right of q2 (i.e., x>8)
1. Left of q1:
- If q3 is positive, it will be repelled by q1 and attracted by q2. The forces will act in opposite directions, potentially balancing each other.
- If q3 is positive, it will be repelled by q1 and attracted by q2. The net force cannot be zero since both forces will act in the same direction.
- If q3 is positive, it will be repelled by q2 and attracted by q1. The forces will act in opposite directions, potentially balancing each other.
Assuming q3 is placed at a distance x from the origin (to the left of q1), the distances to the charges are:
- Distance from q1: |x|
- Distance from q2: 8+|x|
- Force due to q1 on q3:
F1=k|q1⋅q3|x2
- Force due to q2 on q3:
F2=k|q2⋅q3|(8+|x|)2
k12⋅q3x2=k3⋅q3(8+|x|)2
Since k and q3 are common on both sides, they can be canceled out:
12x2=3(8+|x|)2
12(8+|x|)2=3x2
Expanding the left side:
12(64+16|x|+x2)=3x2
768+192|x|+12x2=3x2
Rearranging gives:
9x2+192|x|+768=0
Using the quadratic formula:
x=−b±√b2−4ac2a
where a=9,b=192,c=768:
x=−192±√1922−4⋅9⋅7682⋅9
1922=36864
4⋅9⋅768=27648
√36864−27648=√9216=96
x=−192±9618
Calculating the two possible values:
1. x=−9618=−5.33cm
2. x=−28818=−16cm
The valid position for q3 is x=−16cm (to the left of the origin).
Topper's Solved these Questions
Similar Questions
A point charge q1=4.00nC is placed at the origin, and a second point charge q2=−3.00nC, placed on the x-axis at x = + 20.0 cm. A third point charge q3=2.00nC is placed on the X-axis between q1,andq2. (Take as zero the potential energy of the three charges when they are infinitely far apart).
(a) What is the potential energy of the system of the three charges if q3 is placed at x= + 10.0 cm?
(b) Where should q3 be placed to make the potential energy of the system equal to zero?
View SolutionCharge q1=+6.0nC is on y-axis at y=+3cm and charge q2=−6.0nC is on y-axis at y=−3cm. Calculate force on a test charge q0=2nC placed on X-axis at x=4cm.
View Solution
Knowledge Check
Two point charges 2q and 8q are placed at a distance r apart. Where should a third charge −q be placed between them so that the electrical potential energy of the system is a minimum
Aat a distance of r/3 from 2qBat a distance of 2r/3 from 2qCat a distance of r/16 from 2qDNone of the aboveA charge +q is located at the origin, while an identical charge is located on the x axis at x = +0.50 m. A third charge of +2 q is located on the x axis at such a place that the net electrostatic force on the charge at the origin doubles, its direction remaining unchanged. Where should the third charge be located ?
A+0.50mB+0.71mC−0.50mD−0.71mTwo point charges are located on the x - axis : q1=−e at x=0 and q2=+e at x=a and q3=+e at x=2a.
The total potential energy of the system of three charges.Ae24πε0aBe28πε0aC−e28πε0aD−e24πε0a
A point charge q=−8.0nC is located at the origin. Find the electric field vector at the point x=1.2m,y=−1.6m.
View SolutionTwo charge q and –3q are placed fixed on x–axis separated by distance d. Where should a third charge2q be placed such that it will not experience any force ?
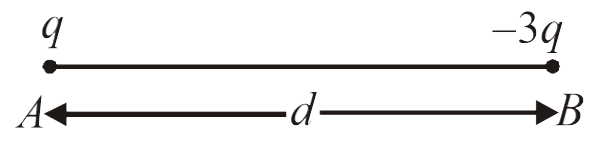
View SolutionTwo charge q and –3q are placed fixed on x–axis separated by distance d. Where should a third charge2q be placed such that it will not experience any force ?

View SolutionA charge of +2μC is placed at x=0 and a charge of −32μc at x=60 .A third charge −Q be placed on the x axis such that it experiences no force .The distance of the point from +2μC is ( in cm)
View SolutionTwo point metal charges−q and +2q are placed at a certain distance apart.Where should a third point charge be placed so that it is in equilibrium?
View Solution
