Two infinitely long straight conductors each having a charge density lamda are arranged parallel to each other. The spearation between them is d. What happens to the force per unit length on each conductor, when the separation between them is doubled?
remains same
doubled
halved
becomes 1/4 th
The correct Answer is:B
To solve the problem, we need to analyze the force per unit length between two infinitely long straight conductors with charge density λ and separated by a distance d. We will then determine what happens to this force when the separation is doubled to 2d.
Step 1: Determine the Electric Field due to One Conductor
The electric field E created by an infinitely long straight conductor with charge density λ at a distance r from it is given by the formula:
E=λ2πϵ0r
where ϵ0 is the permittivity of free space.
Step 2: Calculate the Electric Field at the Location of the Other Conductor
For two parallel conductors, we consider the electric field due to one conductor at the position of the other. If the distance between the conductors is d, the electric field at the location of one conductor due to the other is:
E=λ2πϵ0d
Step 3: Calculate the Force per Unit Length on One Conductor
The force F on a length L of one conductor due to the electric field created by the other conductor can be calculated using:
F=Q⋅E
where Q is the charge on the length L of the conductor. The charge Q can be expressed as:
Q=λL
Thus, the force becomes:
F=λL⋅λ2πϵ0d=λ2L2πϵ0d
To find the force per unit length FL:
FL=λ22πϵ0d
Step 4: Analyze the Effect of Doubling the Separation
Now, if the separation d is doubled to 2d, we need to recalculate the force per unit length. The new electric field at the location of one conductor due to the other will be:
E′=λ2πϵ0(2d)=λ4πϵ0d
The new force F′ on a length L of one conductor is:
F′=Q⋅E′=λL⋅λ4πϵ0d=λ2L4πϵ0d
Thus, the new force per unit length F′L is:
F′L=λ24πϵ0d
Step 5: Compare the Two Forces
Now we can compare the original force per unit length FL and the new force per unit length F′L:
F′L=12⋅FL
This shows that when the separation between the conductors is doubled, the force per unit length on each conductor is halved.
Final Answer
When the separation between the two conductors is doubled, the force per unit length on each conductor is halved.
The electric field E created by an infinitely long straight conductor with charge density λ at a distance r from it is given by the formula:
E=λ2πϵ0r
where ϵ0 is the permittivity of free space.
For two parallel conductors, we consider the electric field due to one conductor at the position of the other. If the distance between the conductors is d, the electric field at the location of one conductor due to the other is:
E=λ2πϵ0d
The force F on a length L of one conductor due to the electric field created by the other conductor can be calculated using:
F=Q⋅E
where Q is the charge on the length L of the conductor. The charge Q can be expressed as:
Q=λL
Thus, the force becomes:
F=λL⋅λ2πϵ0d=λ2L2πϵ0d
To find the force per unit length FL:
FL=λ22πϵ0d
Now, if the separation d is doubled to 2d, we need to recalculate the force per unit length. The new electric field at the location of one conductor due to the other will be:
E′=λ2πϵ0(2d)=λ4πϵ0d
The new force F′ on a length L of one conductor is:
F′=Q⋅E′=λL⋅λ4πϵ0d=λ2L4πϵ0d
Thus, the new force per unit length F′L is:
F′L=λ24πϵ0d
Now we can compare the original force per unit length FL and the new force per unit length F′L:
F′L=12⋅FL
This shows that when the separation between the conductors is doubled, the force per unit length on each conductor is halved.
When the separation between the two conductors is doubled, the force per unit length on each conductor is halved.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBook:NARAYNAChapter:ELECTRIC CHARGES AND FIELDSExercise:EXERCISE -3
Explore 50 Videos
- DUAL NATUREBook:NARAYNAChapter:DUAL NATUREExercise:LEVEL-II (H.W)
Explore 17 Videos
- ELECTRO MAGNETIC INDUCTIONBook:NARAYNAChapter:ELECTRO MAGNETIC INDUCTIONExercise:Level-II (H.W)
Explore 23 Videos
Similar Questions
Two long wires having linear charge density λ and −λ are placed parallel to each other at separation ras shown in the figure. The electric field at point P will be
View SolutionWhat happens to the gravitational force between two objects when the distance between them is:
(i) doubled?
(ii) halved?
View Solution
Knowledge Check
Two infinitely long thin styraight wires having uniform linear charge densities λ and 2λ are arranged parallel to each other at a distance r apart.The intensity of the electric field at a point midway between them is
A2λπε0Bλπε0rCλ2πε0rD3λ2πε0rTwo long and straight conductors, placed parallel to each other are separated by 10 cm, carrying current of 2A and 4 A respectively in opposite direction. The force per unit length exerted by each conductor on the other
A16×10−5 N/mB1.6×10−5 N/mC32×10−4 N/mD3.2×10−5 N/mThe graph of force per unit legth between two long parallel current carrying conductors and the reciprocal of the distance between them is
AStraight lineBParabolaCEllipseDRectangular hyperbola
Two identical long metal wires having radius a are held parallel to each other at a separation d(>>a). Calculate the capacitance of the system per unit length.
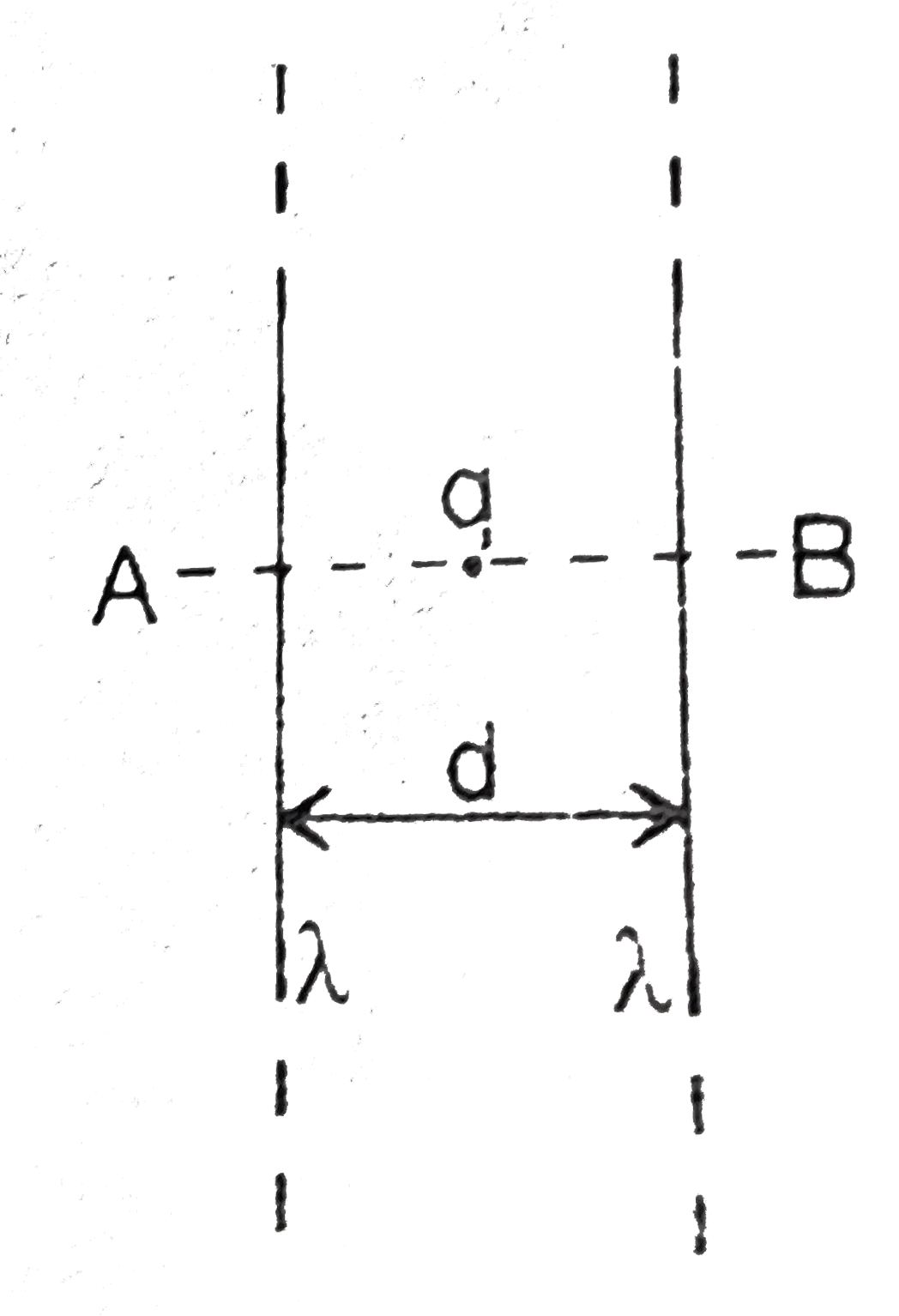
View SolutionTwo infinitely long line charges having charge density λ each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and λq>0 Neglect gravity. Find the time period.
View SolutionTwo long straight parallel wires carry charges λ1andlamba2 per unit length. The distance between them is d. Calculate the magnitude of force externed on the length of one due to charge on the other.
View SolutionThree long straight conductors are arranged parallel to each other in the same plane and carryin currents of 1A,2A and3A all in the same direction. The distance betweent eh first two conductros is x and the distance between the second and third conductorsy. If the middle conductor is in equilibrium, the ratio x:y is
View SolutionTwo charges each of 1μC are at 3 cm. Then the force between them is
View Solution