A dipole with an electric moment p is located at a distance r from a along thread charge uniformly with a linear density λ. Find the force F acting on the dipole if the vector p is oriented
(a) along the thread
(b) along the radius vector r
(c ) at the right angles to the thread and the radius vector r.
The correct Answer is:(a) F=0 ; (b) F=−λp2πε0r2 ; (c ) F=λp2πε0r2
Step by step video, text & image solution for A dipole with an electric moment p is located at a distance r from a along thread charge uniformly with a linear density lambda. Find the force F acting on the dipole if the vector p is oriented (a) along the thread (b) along the radius vector r (c ) at the right angles to the thread and the radius vector r. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct Answer Type
24 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct Answer Type
1 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Comprehension Type
2 Videos
- COMMUNICATION SYSTEMBOOK - CENGAGE PHYSICSCHAPTER - COMMUNICATION SYSTEMEXERCISE - QUESTION BANK
19 Videos
- Current ElectricityBOOK - CENGAGE PHYSICSCHAPTER - Current ElectricityEXERCISE - QUESTION BANK
40 Videos
Similar Questions
An electric dipole of moment p is kept at a distance r form an infinte long charged wire of linear charge density λ as shown.Find the force acting on the dipole?

View SolutionA dipole of electric moment p is located at a distance r from a long thread charged with a linear density λ . Find the force on the dipole if (a) if is placed parallel to the thread , (b) perpendicular to the thread .
[Hint : Field due to long thread = 12πε0λr]
View Solution
Knowledge Check
As shown in the figure an electric dipole lies at a distance x from the centrr of a chargerd ring of radius R with charge Q uniformly distributed over it .The net force acting on the dipole is
 AaQq4πε0R2−2x22πε0(R2+x2)5/2BaQq2πε0R2+2x22πε0(R2+x2)5/2CaQq4πε0R2+2x22πε0(R2+x2)5/2DaQq2πε0R2−2x22πε0(R2+x2)5/2
AaQq4πε0R2−2x22πε0(R2+x2)5/2BaQq2πε0R2+2x22πε0(R2+x2)5/2CaQq4πε0R2+2x22πε0(R2+x2)5/2DaQq2πε0R2−2x22πε0(R2+x2)5/2Electric field at a point of distance r from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to
Ar−1BrCr2Dr−2A tiny electric dipole of dipole moment p is palced at a distance r from an infinitely long wire, with its →p normal to the wire. If the linear charge density of the wire is λ, the electrostatic force acting on the dipole is equal to
AλP4πε0rBλPπε0rC2λPπε0rDλP2πε0r2
A point dipole with an electric moment p is located at a distance l from an infinite conducting plane. Find the modulus of the vector of the force acting on the dipoel if the vector p is perpendicular to the plane.
View SolutionA point charge q is placed at a distance r from a very long charged thread of unoform linear charge density λ. Find out total electric force experienced by the line charge due to the point charge. (Neglect gravity).
View SolutionA point charge q is placed at a distance r from a very long charged thread of unoform linear charge density λ. Find out total electric force experienced by the line charge due to the point charge. (Neglect gravity).
View SolutionAn electric dipole is placed at a distance x from centre O on the axis of a charged ring of R and charge Q uniformly distributed over it.
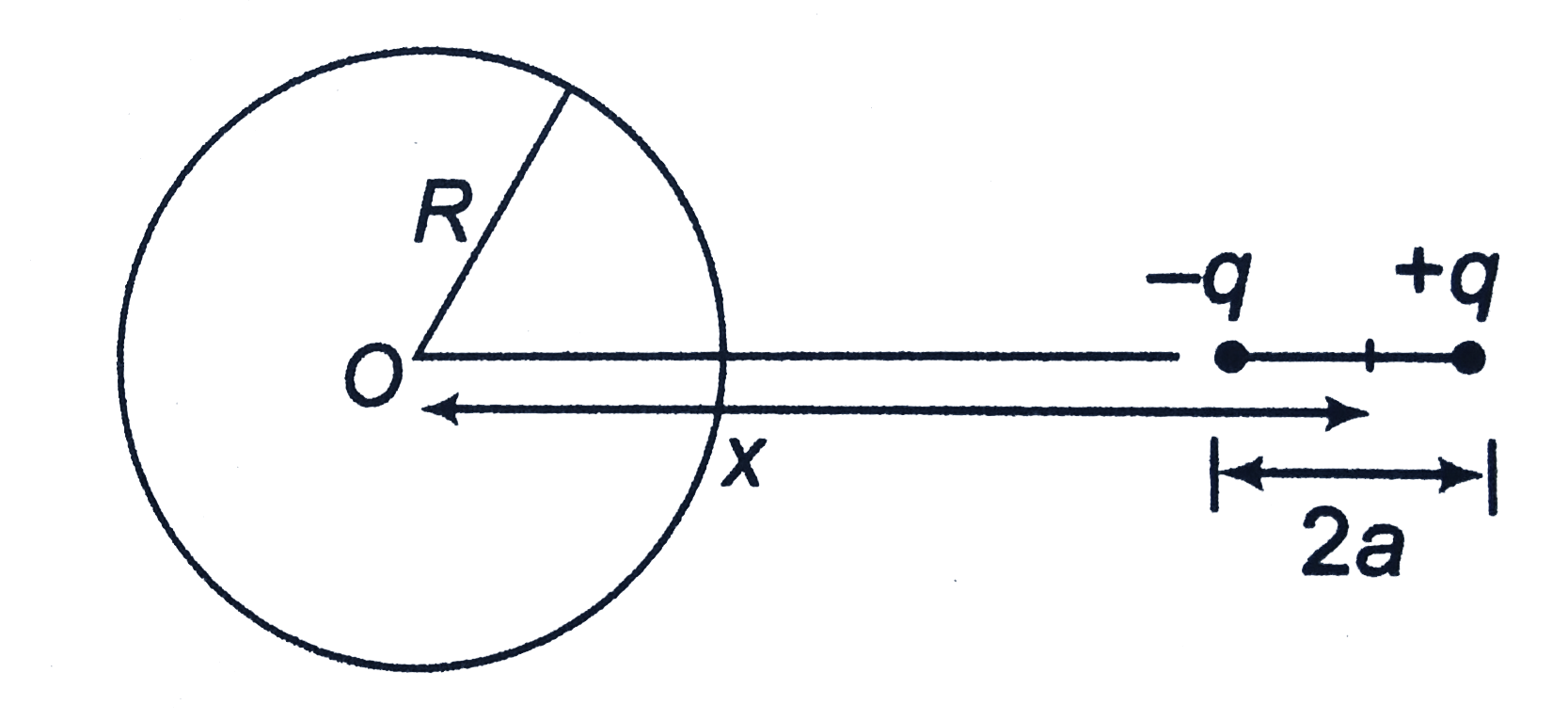
(a) Find the net force acting on the dipole.
(b) What is the work done in rotating the dipole through 180∘?
View SolutionA small current-carrying loop is located at a distance r from a long straight conductor with current I. The magnetic moment of the loop is equal to pm. Find the magnitude and direction of the force vector applied to the loop if the vector pm
(a) is parallel to the stratight conductor,
(b) is oriented along the radius vector r,
(c) coincides in direction with the magnetic field produced by the current I the point where the loop is located.
View Solution
