A small current-carrying loop is located at a distance r from a long straight conductor with current I. The magnetic moment of the loop is equal to pm. Find the magnitude and direction of the force vector applied to the loop if the vector pm
(a) is parallel to the stratight conductor,
(b) is oriented along the radius vector r,
(c) coincides in direction with the magnetic field produced by the current I the point where the loop is located.
Due to the straight conductor, Bφ=μ0I2πr
We use the formula, →F=(−→pm.→∇)→B
(a) The vector −→pm is parallel to the staright conductor.
→F=pm∂∂Z→B=0,
because netiher the direction nor the magnitude of →B depends on z
(b) The vector −→pm is oriented along the radius vector →r
→F=pm∂∂r→B
The direction of →B at r+dr is parallel to the direction at r. Thus only the φ component of →F will survive.
Fφ=pm∂∂rμ0I2πr=−μ0Ipm2π2
(c) The vector −→pm coincides in direction with the magnetic field, produced by the conductor carrying current I
→F=pm∂r∂φμ0I2π→eφ=μ0Ipm2πr2∂→eφ∂φ
So, →F=μ0Ipm2πr2→er As, ∂→eφ∂φ=−→er
Topper's Solved these Questions
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Electromagnetic Induction
Explore 84 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Motion Of Charged Particle In Magnetic Field
Explore 36 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Electric Current
Explore 72 Videos
- ELECTRICITY AND MAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRICITY AND MAGNETISMExercise:All Questions
Explore 6 Videos
- ELECTROMAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTROMAGNETISMExercise:All Questions
Explore 24 Videos
Similar Questions
A small current-carrying coil having a megantic moment pm is located at the axis of a round loop of radius R with current I flowing thorough it. Find the magnitude of the vector force applied to the coil if its distance from the centre of the loop is equal to x and the vector pm coincides in direction with the axis of the loop.
View SolutionA rectangular loop carryinig current I is located near an infinite long straight conductor carrying current I as shown in the figure. The loop,

View Solution
Knowledge Check
A circular loop of radius 0.05 m carries a current of 1.0 A. The magnetic moment of the loop is .
A1.32×10−4A−m2B7.85×10−4A−m2C2.62×10−4A−m2D5.25×10−4A−m2A square loop of ABCD carrying a current i, is placed near and coplanar with a long straight conductor XY carrying a current I, the net force on the loop will be
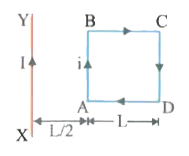 A2μ0li3πBμ0li2πC2μ0liL3πDμ0liL2π
A2μ0li3πBμ0li2πC2μ0liL3πDμ0liL2πA square loop ABCD carrying a current i, is placed near and coplanar with a long straight conductor XY carrying a current I, the net force on the loop will be
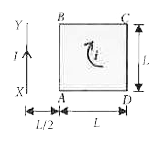 A2m0liL3πBμ0liL2πC2μ0Ii3πDμ0Ii2π
A2m0liL3πBμ0liL2πC2μ0Ii3πDμ0Ii2π
A square loop of ABCD carrying a current i, is placed near and coplanar with a long straight conductor XY carrying a current I, the net force on the loop will be

View SolutionMagnetic induction produced at the center of a circular loop of radius R carrying a current is 'B' The magnetic moment of the loop is
View Solution
A square loop ABCD carrying a current i is placed near and coplanar with a long straight conductor XY carrying a current I.
View SolutionA square loop ABCD , carrying a current I, is placed near and coplanar with a long straight conductor XY carrying a current I.

View SolutionA long straight conductor carrying a current i is bent to form an almost complete circular loop of radius r on it. The magnetic field at the centre of the loop

View Solution

