Find the area of the region bounded by the curve $y^{2} = 2 x and x^{2} + y^{2} = 4 x$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:N/a

We have, $y^{2} = 2 x and x^{2} + y^{2} = 4 x$

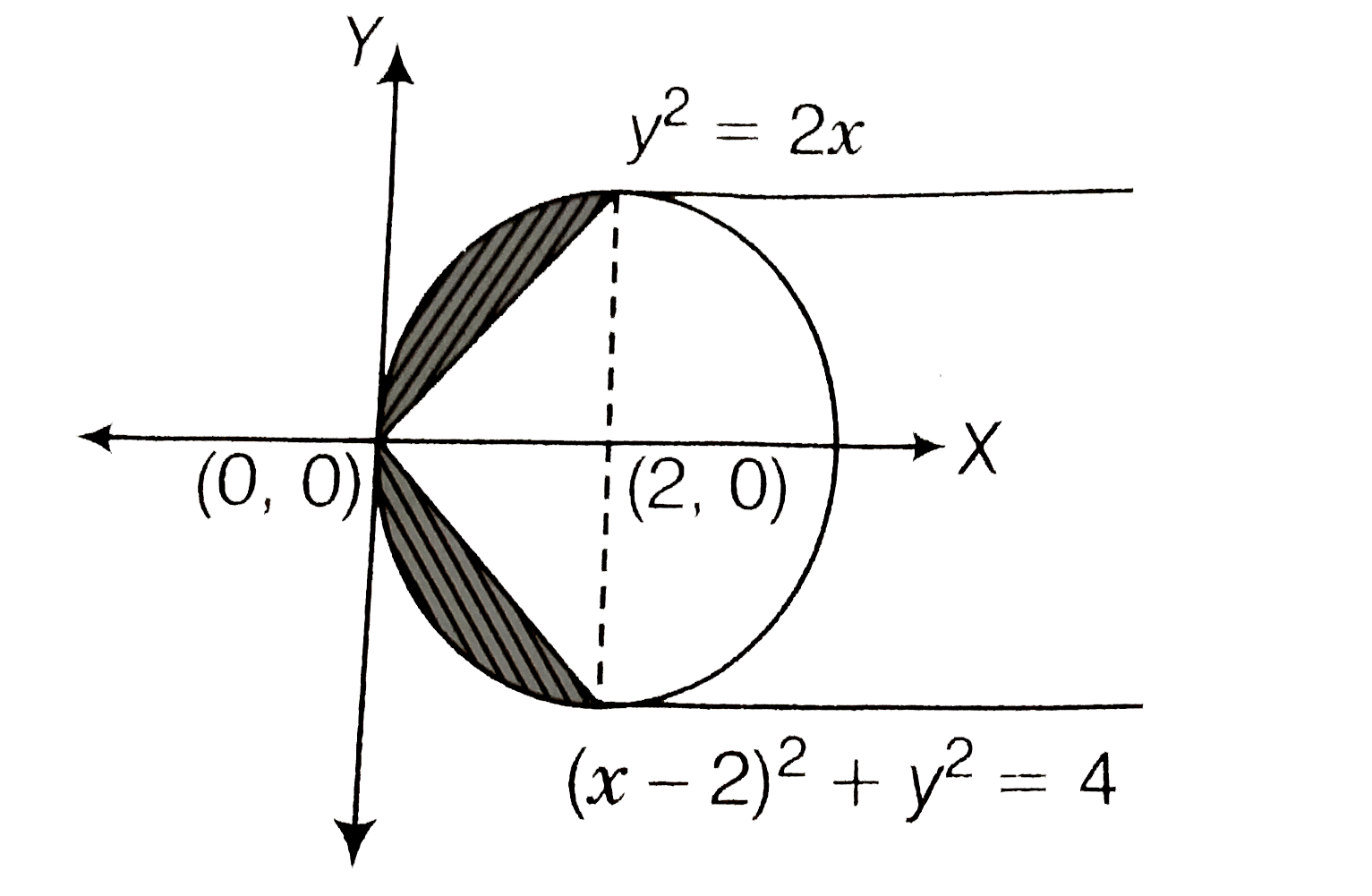
$\Rightarrow x^{2} + 2 x - 4 x$
$\Rightarrow x^{2} - 2 x = 0$
$\Rightarrow x (x - 2) = 0$
$\Rightarrow x = 0, 2$
Also, $x^{2} + y^{2} = - y^{2}$
$\Rightarrow x^{2} - 4 x = - y^{2}$
$\Rightarrow x^{2} - 4 x + 4 = - y^{2} + 4$
$\Rightarrow {(x - 2)}^{2} - 2^{92}) = - y^{2}$
$∴ Required area = 2 . \int_{0}^{2} [\sqrt{2^{2} - {(x - 2)}^{2}} - \sqrt{2 x}] d x$
$= 2 ⎡ ⎣ {[\frac{x - 2}{2} . \sqrt{2^{2} - {(x - 2)}^{2}} + \frac{2^{2}}{2} {sin}^{- 1} (\frac{x - 2}{2})]}_{0}^{2} - {[\sqrt{2} . \frac{x^{3 / 2}}{3 / 2}]}_{0}^{2} ⎤ ⎦$
$= 2 [(0 + 0 - 1.0 + 3 . \frac{π}{2}) - \frac{2 \sqrt{2}}{3} (2^{3 / 2 - 0})]$
$= \frac{4 π}{2} - \frac{8.2}{3} = 2 π - \frac{16}{3} = 2 (π - \frac{8}{3}) sq units$

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Find the area of the region bounded by the curve $y^{2} = 4 x and x^{2} = 4 y$ .
A $\frac{15}{7} sq units$
B $\frac{16}{7} sq units$
C $\frac{16}{3} sq units$
D $16 sq units$
The area of the region bounded by the curves $y = x^{2} and x = y^{2}$ is
A $\frac{1}{3}$
B $\frac{1}{2}$
C $\frac{1}{4}$
D3
The area of the region bounded by the curves $x = y^{2} - 2$ and x=y is
A $\frac{9}{4}$
B9
C $\frac{9}{2}$
D $\frac{9}{7}$

NCERT EXEMPLAR-APPLICATION OF INTEGRALS-Application Of Integrals

Home
Ask Doubt
Profile