Find the area of the region ${(x, y) : y^{2} \leq 6 a x and x^{2} + y^{2} \leq 16 a^{2}}$ using method of integration .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:N/a

We have, $y^{2} = 6 a x and x^{2} + y^{2} = 16 a^{2}$
$\Rightarrow x^{2} + 16 a x - 16 a^{2} = 0$
$\Rightarrow x^{2} + 8 a x - 2 a x - 16 a^{2} = 0$
$\Rightarrow x (x + 8 a) - 2 a (x + 8 a) = 0$
$\Rightarrow (x - 2 a) (x + 8 a) = 0$
$\Rightarrow x = 2 a, - 8 a$

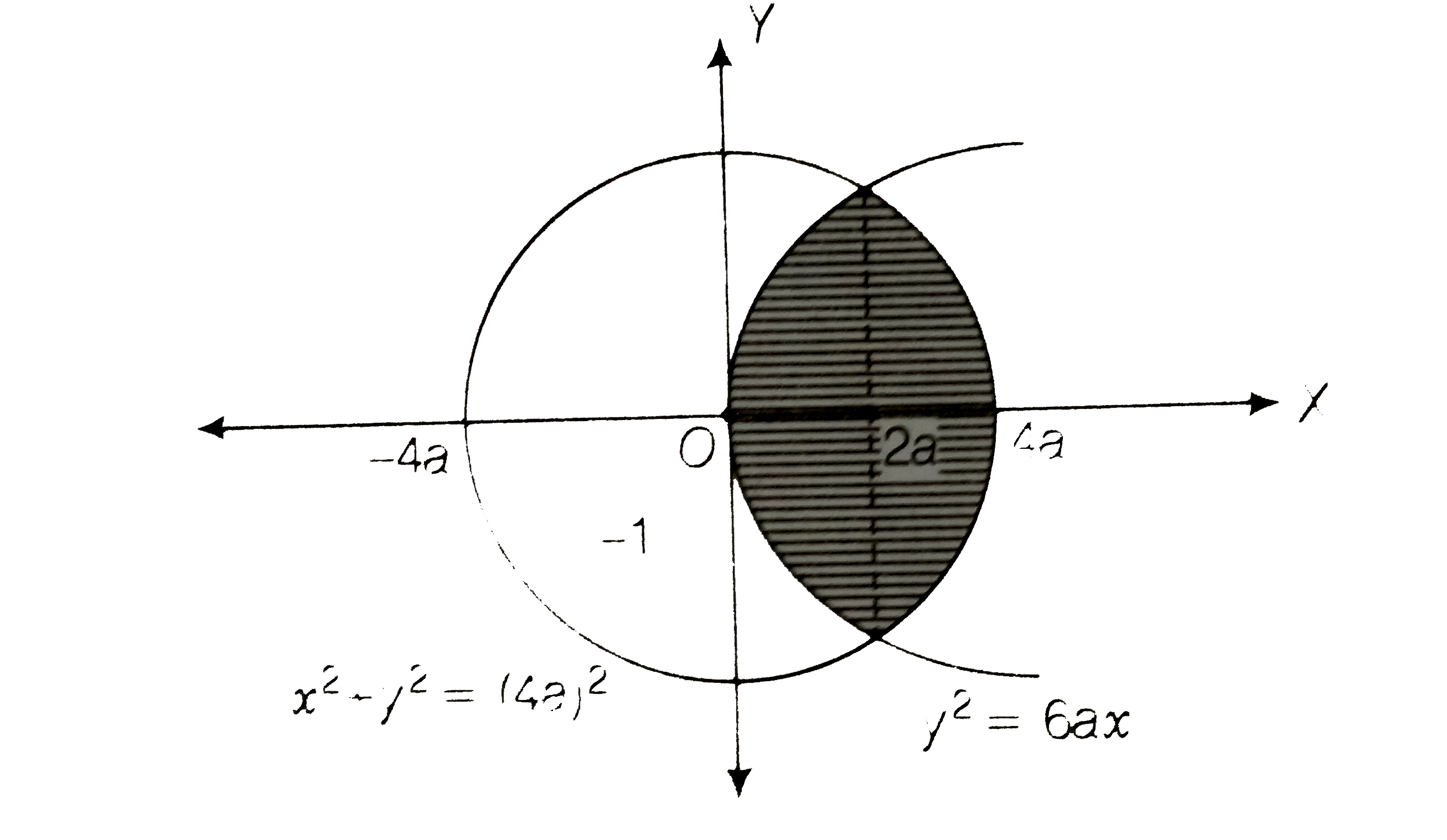
$∴ Area of required region = [\int_{0}^{2 a} \sqrt{6 a x} d x + \int_{2 a}^{4 a} \sqrt{{(4 a)}^{2} - x^{2} d x}]$
$= 2 [\int_{0}^{2 a} \sqrt{6 a} x^{1 / 2} d x + \int_{2 a}^{4 a} \sqrt{{(4 a)}^{2} - x^{2}} d x]$
$= 2 ⎡ ⎣ \sqrt{6 a} {[\frac{x^{3 / 2}}{3 / 2}]}_{0}^{2 a} + {(\frac{x}{2} \sqrt{{(4 a)}^{2} - x^{2}} + \frac{{(4 a)}^{2}}{2} {sin}^{- 1} . \frac{x}{4 a})}_{2 a}^{4 a} ⎤ ⎦$
$= 2 [\sqrt{6 a} . \frac{2}{3} ({(2 a)}^{3 / 2} - 0) + \frac{4 a}{2} .0 + \frac{16^{2}}{2} . \frac{π}{2} - \frac{2 a}{2} \sqrt{16 a^{2} - 4 a^{2}} - \frac{16 a^{2}}{2} . {sin}^{- 1} . \frac{2 a}{4 a}]$
$= 2 [\sqrt{\cdot 6 a} \frac{2}{3} .2 \sqrt{2} a^{3 / 2} + 0 + 4 π a^{2} - \frac{2 a}{2} . \sqrt{3} a - 8 a^{2} . \frac{π}{6}]$
$= 2 [\sqrt{12} \frac{.4}{3} a^{2} + 4 π a^{2} - 2 \sqrt{3} a^{2} - \frac{4 a^{2} π}{3}]$
$= 2 [\frac{8 \sqrt{3} a^{2} + 12 π a^{2} - 6 \sqrt{3} a^{2} - 4 a^{2} π}{3}]$
$= \frac{2}{3} a^{2} [8 \sqrt{3} + 12 π - 6 \sqrt{3} a^{2} - 4 a^{2} π]$
$= \frac{2}{3} a^{2} [2 \sqrt{3} + 8 π] = \frac{4}{3} a^{2} [\sqrt{3} + 4 π]$

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

NCERT EXEMPLAR-APPLICATION OF INTEGRALS-Application Of Integrals

Home
Ask Doubt
Profile