Area of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle x2+y2=32 is
16π sq units
4π sq units
32π sq units
24π sq units
The correct Answer is:B
We have, area enclosed by X-axis i.e., y = 0, y = x and the circle x2+y2=32 in first quadrent.
Since, x2+(x)2=32[∵y=x]
⇒22=32
⇒x=±4
So, the intersection point of circle x2+y2=32 and line y=x are (4,4) or (−4,4).
and x2+y2=(4√2)2
Since, y=0
∴x2+(0)2=32
⇒x=±4√2
So, the circle intersects the X-axis at (±4√2,0).
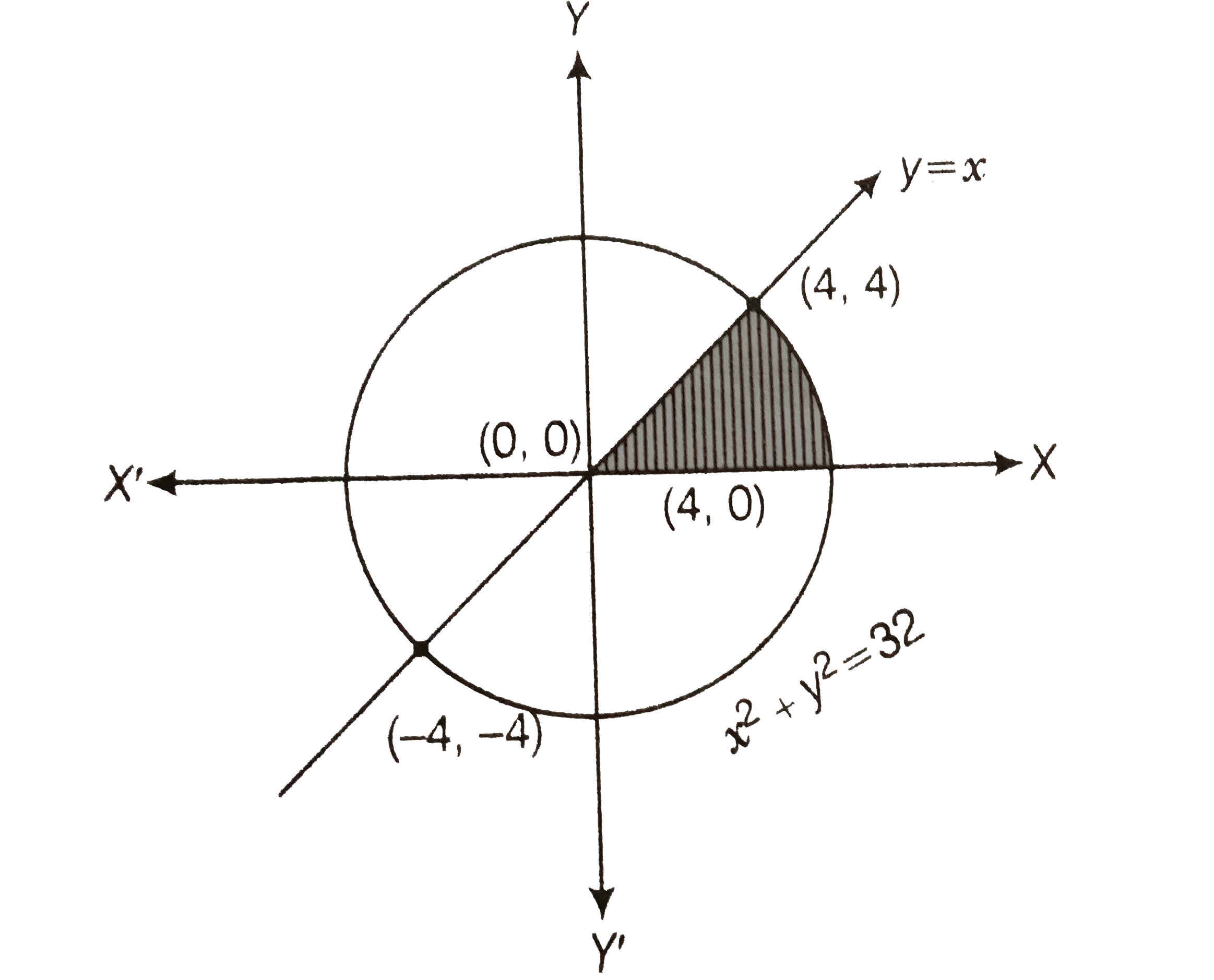
Area of shaded region =4∫0xdx+4√2∫4√(4√2)2−x2dx
=∣∣∣x22∣∣∣40+∣∣
∣
∣∣x2√(4√2)2−x2+(4√2)22sin−1.x4√2∣∣
∣
∣∣4√24
=162+⎡⎢
⎢⎣4√22.0+16sin−1.(4√2)(4√2)−42√(4√2)2−16−16sin−1.44√2⎤⎥
⎥⎦
=8+[16.π2−2.√16−16.π4]
=8+[8π−8−4π]=4π sq units
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the area of region in the first quadrant enclosed the X-axis, the line y =x and the circlex2+y2=32.
A4π sq unitsB3π sq unitsC5π sq unitsDNone of theseConside the line x=√3y and the circle x2+y2=4
What is the area of the region in the first quadrant enclosed by the X-axis, the line =√3y and the circle?Aπ3Bπ6Cπ3−√32DNone of the above
Find the area of the region in the first quadrant enclosed by the x-axis, the line y=x and the circle x2+y2=32.
View SolutionFind the area of the region in first quadrant enclosed by the x-axis, the line y=2x and the circle x2+y2=24.
View SolutionFind the area of the region in the first quadrant enclosed by x−aξs, the line x=√3 y and the circle x2+y2=4.
View SolutionLet A be the area of the region in the first quadrant bounded by the x-axis the line 2y = x and the ellipse x29+y21=1. Let A' be the area of the region in the first quadrant bounded by the y-axis the line y = kx and the ellipse . The value of 9k such that A and A' are equal is _____
View SolutionFind the area of the region in the first quadrant enclosed by x=y2andx=y+2
View SolutionThe area of the region lying in the first quadrant and bounded by the curve y=4x2, and the lines y =2 and y =4 is "___________"
View Solution