The area of the region bounded by the curve y = sin x between the ordinates x=0,x=π2 and the X-axis is
A
2 sq units
B
4 sq units
C
3 sq units
D
1 sq unit
Video Solution
Text Solution
The correct Answer is:D
Area of the bounded by the curve t=sinx between the ordinates x=0,x=π2 and the X-axis is
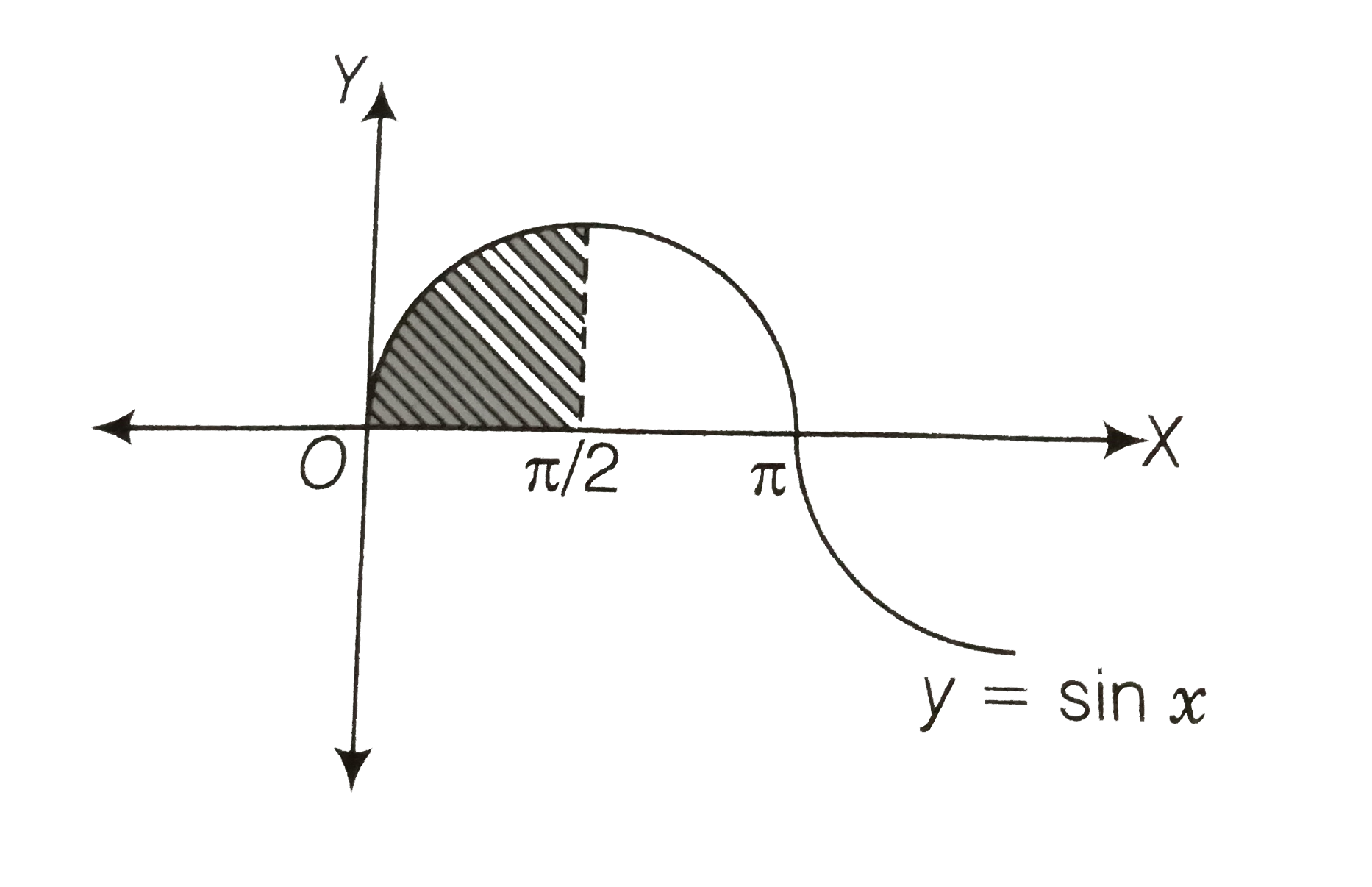
A=∫π/20sinxdx
=−[cos]π/20=−[cos.π2−cos0]
=−[0−1]=1 sq unit
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The area (in square units) bounded by curves y=sinx between the ordinates x=0, x=π and the x-axis , is
A2B4C3D1 - Question 2 - Select One
The area of the region bounded by the curve y=cosx, X-axis and the lines x=0, x=2π is
A2B4C0D3 - Question 3 - Select One
The area bounded by the curves y = cos x and y = sin x between the ordinates x = 0 and x=3π2, is
A4√2+1B4√2−1C4√2+2D4√2−2
The area of the region bounded by the curve y=sinx,x−aξs and the ordinates x=0,x=π3 is
View SolutionFind the area of the region bounded by the curve C:y=tanx,tan≥ntdrawn→C at x=π4, and the x-axis.
View Solutionthe are of the region bounded by the curve y=(x2+2)2+2x and the ordinates x−0,x=2.
View SolutionThe area of the region bounded by the curve y=2x+3 ,x-axis and the lines x=0 and x=2 is
View SolutionThe area of the region bounded by the curves y=sinx,y=sin2x and ordinates x=π to x=2π is
View Solution

