Compute the area bounded by the lines x+2y=2;y−x=1 and 2x+y=7
Video Solution
Text Solution
The correct Answer is:N/a
We have, x+2y=2…(i)
y−x=1…(ii)
and 2x+y=7…(iii)
On solving Eqs. (i) and (ii), we get
y−1(2−2y)=1⇒3y−2=1⇒y=1

2(y−1)+y=7
On solving Eqs. (ii) and (iii), we get
⇒2y−2+y=7
⇒y=3
On solving Eqs. (i) and (iii) , we get
2(2−2y)+y=7
4−4y+y=7
⇒−3y=3
⇒y=−1
∴ Required area =∫1−1(2−2y)dy+∫3−1(7−y)2dy−∫31(y−1)dy
[−2y+2y22]1−1+[7y2−y22.2]3−1−[y22−y]31
=[−2+22−2−22]+[212−94+72+14]−[92−3−12+1]
=[−4]+[42−9+14+14]−[9−6−1+22]
=−4+12−2=6 sq units
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Area bounded by the lines x=2y,y=2x and x = 4 is
A14B13C10D12Area bounded by the lines y=2x,y=4x and x = 2 is
A8B4C5DNone of theseThe area bounded by the curves y=x2andy=2−x2 is
A83 sq unitsB3/8 sq unitsC3/2 sq unitsDNone of these
Compute the area of the figure bounded by the lines y=x+1,y=cosx and the x-axis
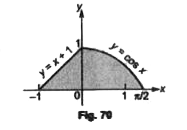
View SolutionThe area bounded by the lines y=|x−2|,|x|=3 and y=0 is
View SolutionCompute, using integration, the area bounded by the lines Given lines x+2y=2,y−x=1,2x+y=7 is
View SolutionThe area bounded by the curve y=2x−x2 and the line y = - x is
View SolutionThe area bounded by the curves y2=x3and|y|=2x is
View Solution
