The area bounded by the lines y=||x−1|−2| and x axis is
The correct Answer is:8
To find the area bounded by the curve y=||x−1|−2| and the x-axis, we will follow these steps:
Step 1: Understand the function
The function y=||x−1|−2| involves absolute values, which means we need to break it down into different cases based on the values of x.
Step 2: Break down the absolute values
1. First absolute value: |x−1|
- For x<1: |x−1|=1−x
- For x≥1: |x−1|=x−1
2. Second absolute value: ||x−1|−2|
- We need to consider the cases based on the first absolute value's output.
Step 3: Analyze cases for ||x−1|−2|
1. Case 1: x<−1
- |x−1|=1−x → ||x−1|−2|=|(1−x)−2|=|−x−1|=x+1
2. Case 2: −1≤x<3
- |x−1|=1−x → ||x−1|−2|=|(1−x)−2|=|−x−1|=x+1
3. Case 3: x≥3
- |x−1|=x−1 → ||x−1|−2|=|(x−1)−2|=|x−3|
- For x≥3: ||x−1|−2|=x−3
Step 4: Find the points of intersection with the x-axis
To find the area bounded by the curve and the x-axis, we need to find where y=0.
1. From the analysis:
- For x<−1: x+1=0 → x=−1
- For −1≤x<3: x+1=0 → x=−1 (already found)
- For x≥3: x−3=0 → x=3
Thus, the points of intersection with the x-axis are x=−1 and x=3.
Step 5: Determine the area
The area bounded by the curve and the x-axis can be calculated by integrating the function from x=−1 to x=3.
1. Area Calculation:
- For −1≤x<3: y=x+1
- For x≥3: y=x−3 (but this part does not contribute to the area since it is above the x-axis)
The area can be calculated as:
Area=∫3−1(x+1)dx
Step 6: Calculate the integral
Area=(x22+x)3−1
Calculating the definite integral:
=(322+3)−((−1)22−1)
=(92+3)−(12−1)
=(92+62)−(12−22)
=152−(−12)
=152+12=162=8
Final Answer
The area bounded by the curve and the x-axis is 8.
---
The function y=||x−1|−2| involves absolute values, which means we need to break it down into different cases based on the values of x.
1. First absolute value: |x−1|
- For x<1: |x−1|=1−x
- For x≥1: |x−1|=x−1
- We need to consider the cases based on the first absolute value's output.
1. Case 1: x<−1
- |x−1|=1−x → ||x−1|−2|=|(1−x)−2|=|−x−1|=x+1
- |x−1|=1−x → ||x−1|−2|=|(1−x)−2|=|−x−1|=x+1
- |x−1|=x−1 → ||x−1|−2|=|(x−1)−2|=|x−3|
- For x≥3: ||x−1|−2|=x−3
To find the area bounded by the curve and the x-axis, we need to find where y=0.
- For x<−1: x+1=0 → x=−1
- For −1≤x<3: x+1=0 → x=−1 (already found)
- For x≥3: x−3=0 → x=3
The area bounded by the curve and the x-axis can be calculated by integrating the function from x=−1 to x=3.
- For −1≤x<3: y=x+1
- For x≥3: y=x−3 (but this part does not contribute to the area since it is above the x-axis)
Area=∫3−1(x+1)dx
Area=(x22+x)3−1
Calculating the definite integral:
=(322+3)−((−1)22−1)
=(92+3)−(12−1)
=(92+62)−(12−22)
=152−(−12)
=152+12=162=8
The area bounded by the curve and the x-axis is 8.
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - (SECTION - A)
20 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - (SECTION - B)
10 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
100 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - QUESTION
1 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
454 Videos
Similar Questions
Knowledge Check
Area bounded by the lines y=x,x=−1,x=2 and x-axis is
A5/2 sq unitB3/2 sq unitC1/2 sq unitDNone of the aboveThe area bounded by the parabola y=4x−x2 and X-axis is
A43sq.unitsB83sq.unitsC163sq.unitsD323sq.unitsThe area bounded by the line y = x, X-axis and the lines x = -1, x = 2 is
A52sq.unitsB32sq.unitsC13sq.unitsD23sq.units
Compute the area of the figure bounded by the lines y=x+1,y=cosx and the x-axis
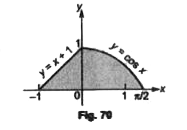
View SolutionThe area of the figure bounded by right of the line y=x+1,y=cosx and x-axis is :
View SolutionCompute the area bounded by the lines x + 2y = 2 , y -x = 1 and 2x + y = 7.
View SolutionThe area of the region bounded by the curve y2=xand the Y axis in the first quadrant and lines y=3andy=9 is ______
View SolutionFind the area of the region bounded by the line y=3x+2, the x-axis and the ordinates x=−1 and x=1
View Solution
