Find the area enclosed by the curve y=−x2 and the straight line x+y+2=0.
Video Solution
Text Solution
The correct Answer is:N/a
We have, y=−x2 and x+y+2=0
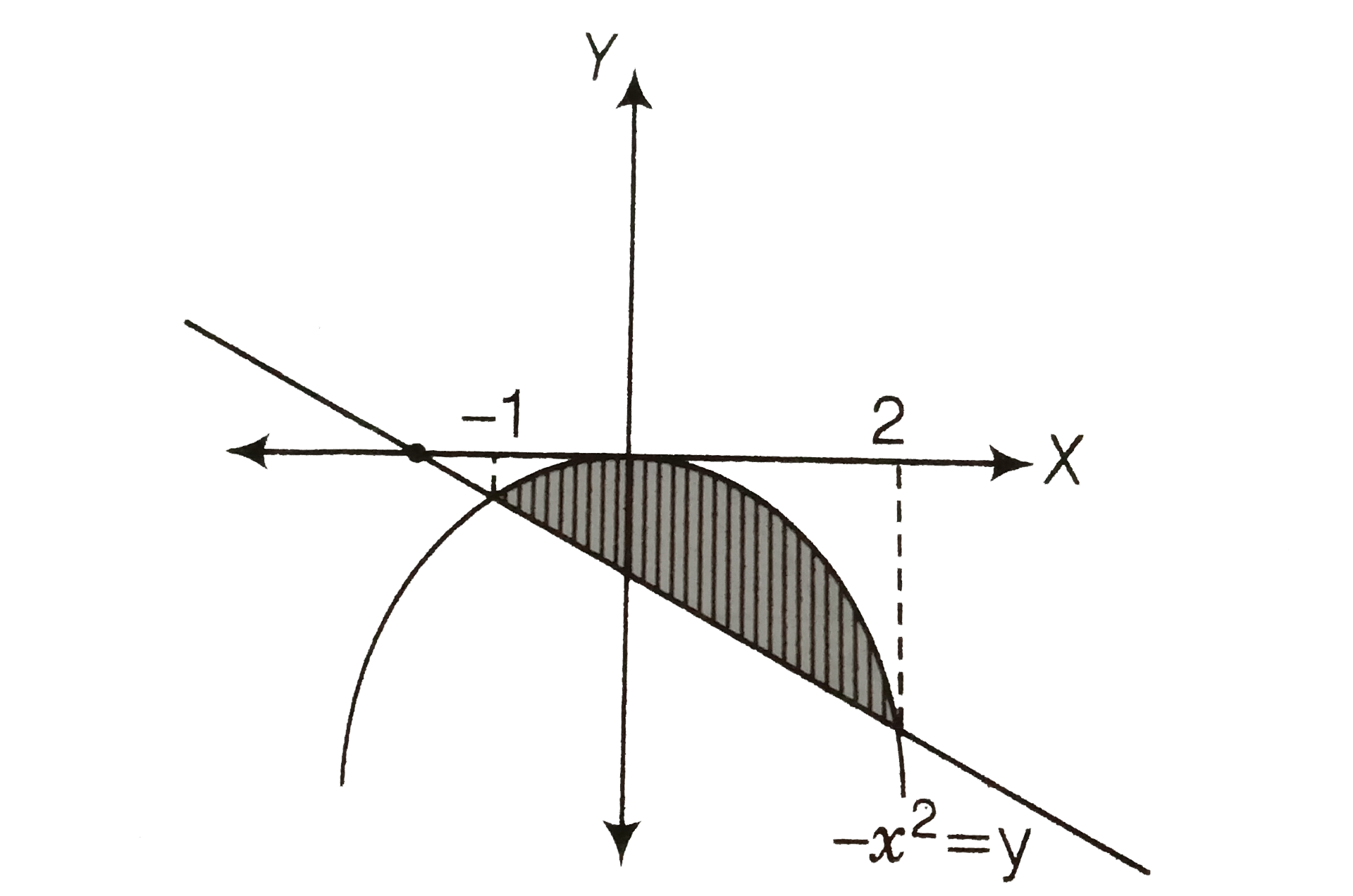
⇒−x−2=−x2⇒x2−x−2=0
⇒x2+x−2x−2=0⇒x(x+1)−2(x+1)=0
⇒(x−2)(x+1)=0⇒x=2,−1
∴Area of shaded region, A=∣∣∣∫2−1(−x−2+x2)dx∣∣∣=∣∣∣∫2−1(x2−x−2)dx∣∣∣
=∣∣
∣∣[x33−x22−2x]2−1∣∣
∣∣=∣∣∣[83−42−4+13+12−2]∣∣∣
=∣∣∣16−12−24++3−126∣∣∣=∣∣∣−276∣∣∣=92 sq units
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
What is the area of the region enclosed between the curve y2=2x and the straight line y=x?
A2/3 sq unitB4/3sq unitC1/3 sq unitD1 sq. unit
Find the area enclosed by the parabola y=2−x2 and the straight line x + y = 0
View SolutionFind the area enclosed by the curves y=4x2 and y2=2x.
View SolutionFind the area enclosed by the curve x2=4y and the abcissa y=1
View SolutionFind the area bounded by the parabola y=2−x2 and the straight line y+x=0.
View SolutionFind the area enclosed between the circle x2+y2=25 and the straight line x+y=5.
View SolutionFor what value of 'a' is the area bounded by the curve y=a2x2+ax+1 and the straight line y=0. x=0andx=1 the least?
View SolutionFind the area enclosed by the curves x2=y,y=x+2,andx−aξs.
View Solution