Find the area of the region bounded by the curve .
Video Solution
Text Solution
The correct Answer is:N/a
Given wquation of curve are
and
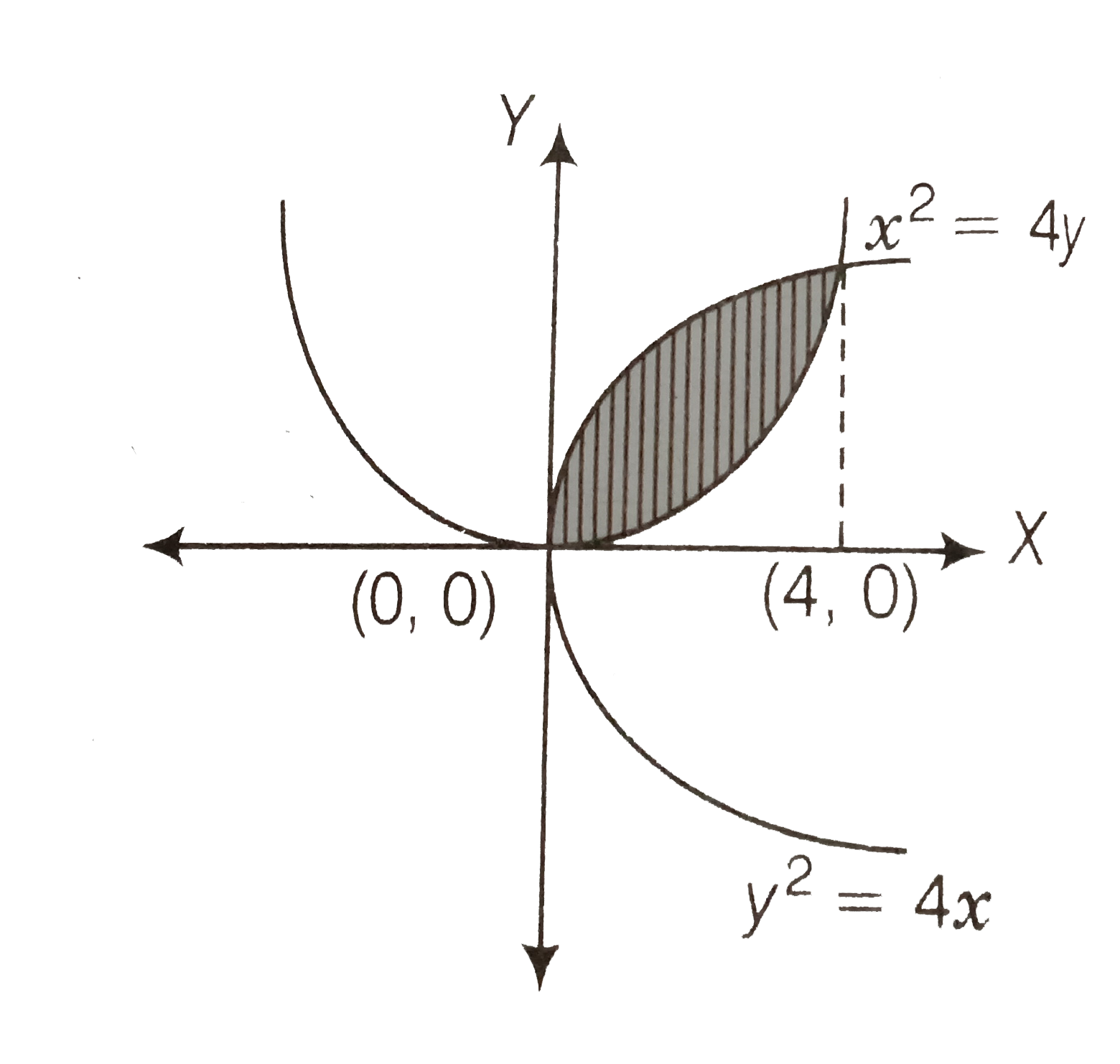
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Find the area of the region bounded by the curve y2=9x and y=3x.
View SolutionFind the area of the region bounded by the curve y2=9x and y=3x.
View SolutionFind the area of the region bounded by the curve y2=2x and x2+y2=4x.
View SolutionFind the area of the region bounded by the curve y2=2x and x2+y2=4x.
View SolutionFind the area of the region bounded by the curves y2=4ax and x2=4ay.
View SolutionFind the area of the region bounded by the curve y2=4x and the line x=3.
View SolutionThe area of the region bounded by the curves y=x2 and x=y2 is
View SolutionFind the area of the region bounded by the curves y2=x+1 and y2=−x+1.
View SolutionFind the area of the region bounded by the curves x2+y2=4 and (x−2)2+y2=4.
View SolutionDraw a rough sketch and find the area of the region bounded by the parabolas y2=4xandx2=4y, using the method of integration.
View Solution


