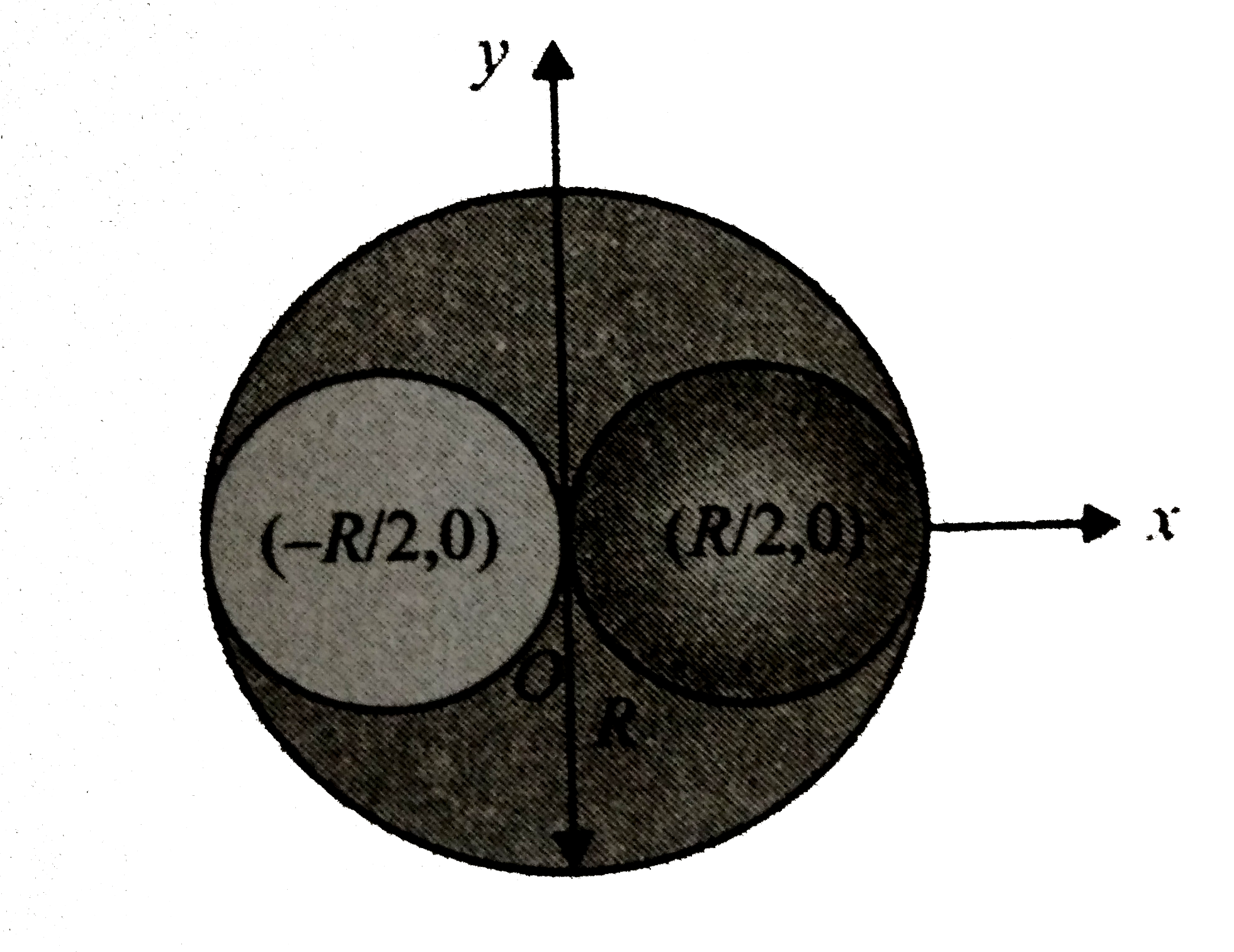
Figure shows a uniform disc of radius R, from which a hole of radius R2 has been cut out from left of the centre and is placed on the right of the centre of the disc. Find the CM of the resulting disc.
R3,0
R2,0
R4,0
R,0
The correct Answer is:C
Step by step video & image solution for Figure shows a uniform disc of radius R, from which a hole of radius R/2 has been cut out from left of the centre and is placed on the right of the centre of the disc. Find the CM of the resulting disc. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 2 (Level-I)
Explore 40 Videos
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 2 (Level-II)
Explore 28 Videos
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 4 Level-II
Explore 20 Videos
- Capacitance Book:MOTIONChapter:Capacitance Exercise:EXERCISE -4 LEVEL II
Explore 19 Videos
- CIRCULAR MOTIONBook:MOTIONChapter:CIRCULAR MOTIONExercise:EXERCISE - 4
Explore 16 Videos
Similar Questions
Find the centre of mass of a unifrom disc of radius a from which a circulr section of radius b has been removed. The centre of hole is at a distance c from the centre of the disc.
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulating flat body.
View Solution
Knowledge Check
Find the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
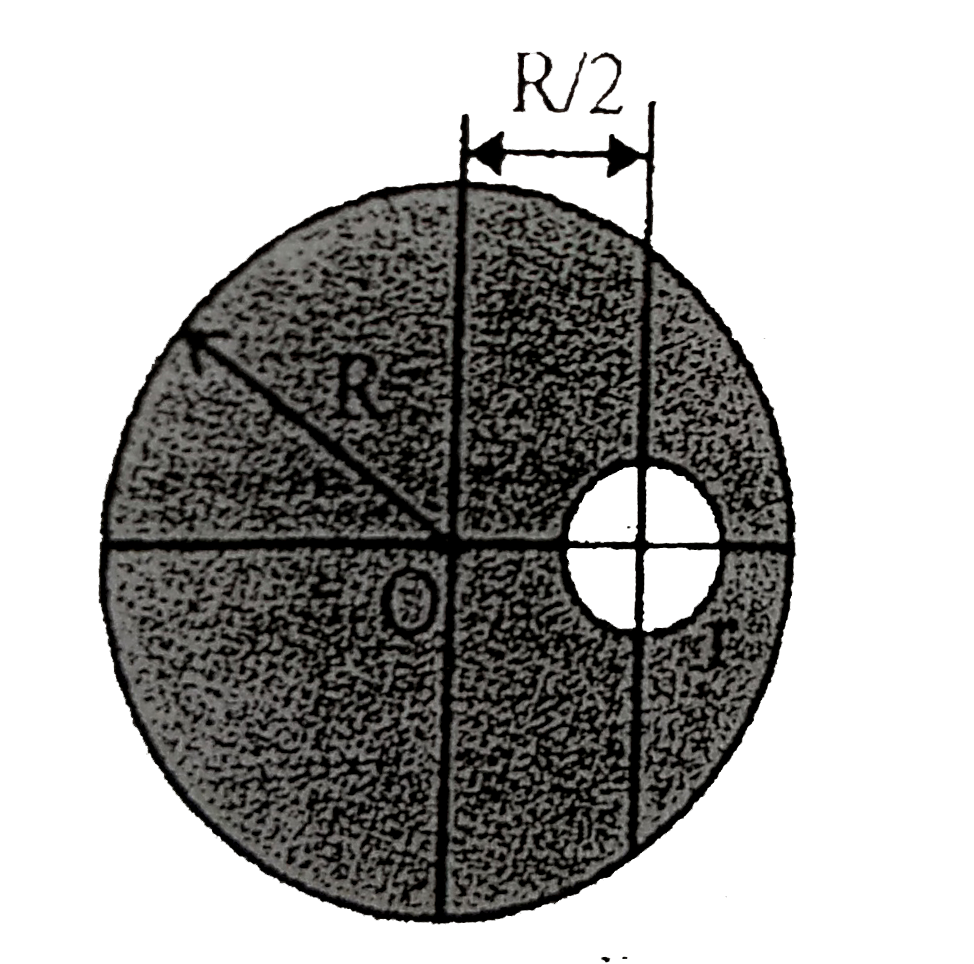 ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of OA paper disc of radius R from which a hole of radius r is cut out is floating in a liquid of the surface tension S. The force on the disc due to the surface tension is
AS×2πRBS×2πrCS×2π(R−r)DS×2π(R+r)From a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −
 A4R3(π−2)B2R3(π−2)C5R7(π−2)DR3(π−1)
A4R3(π−2)B2R3(π−2)C5R7(π−2)DR3(π−1)
The figure shows a disc of radius 3R from which a circular hole of radius R is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point O is
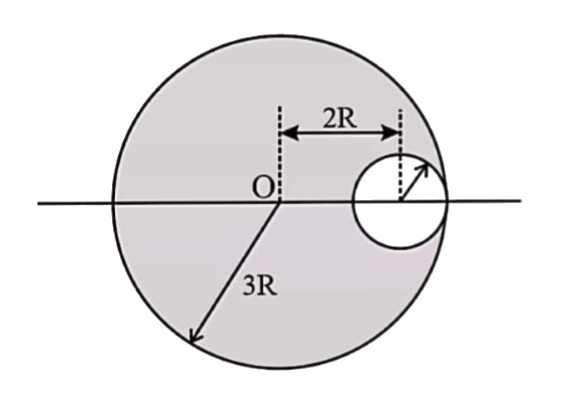
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View SolutionA paper disc of radius R from which a hole of radius r is cut out, is floating in a liquid of surface tension, T. What will be force on the disc due to surface tension?
View SolutionA paper disc of radius R from which a hole of radius r is cut out, is floating n liquid of surface tension, T. What will be force n the disc due to surface tension?
View SolutionFind the centre of mass of a thin, uniform disc of radius R from which a small concentric disc of radius r is cut.
View Solution

